Lesson 3
Making Scaled Copies
3.1: More or Less? (5 minutes)
Warm-up
This warm-up prompts students to use what they know about numbers and multiplication to reason about decimal computations. The problems are designed to result in an answer very close to the given choices, so students must be more precise in their reasoning than simply rounding and calculating.
Whereas a number talk typically presents a numerical expression and asks students to explain strategies for evaluating it, this activity asks a slightly different question because students don't necessarily need to evaluate the expression. Rather, they are asked to judge whether the expression is greater than or less than a given value. Although this activity is not quite the same thing as a number talk, the discussion might sound quite similar.
Launch
Display the problems for all to see. Give students 2 minutes of quiet think time. Tell students they may not have to calculate, but could instead reason using what they know about the numbers and operation in each problem. Ask students to give a signal when they have an answer and a strategy for every problem.
Student Facing
For each problem, select the answer from the two choices.
-
The value of \(25\boldcdot (8.5)\) is:
- More than 205
- Less than 205
-
The value of \((9.93)\boldcdot (0.984)\) is:
- More than 10
- Less than 10
-
The value of \((0.24)\boldcdot (0.67)\) is:
- More than 0.2
- Less than 0.2
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may attempt to solve each problem instead of reasoning about the numbers and operations. If a student is calculating an exact solution to each problem, ask them to look closely at the characteristics of the numbers and how an operation would affect those numbers.
Activity Synthesis
Discuss each problem one at a time with this structure:
- Ask students to indicate which option they agree with.
- If everyone agrees on one answer, ask a few students to share their reasoning, recording it for all to see.
- If there is disagreement on an answer, ask students with differing answers to explain their reasoning and come to an agreement on an answer.
3.2: Drawing Scaled Copies (10 minutes)
Optional activity
Students continue to work with scaled copies of simple geometric figures, this time on a grid. When trying to scale non-horizontal and non-vertical segments, students may think of using tracing paper or a ruler to measure lengths and a protractor to measure angles. Make sure they have a chance to see how the structure of the grid can be useful for scaling the lengths of non-vertical and non-horizonal segments.
To create scaled copies, students need to attend to all parts of the original figure, or else the copy will not be scaled correctly. Use of the grid for scaling non-horizontal and non-vertical segments is a good example of using tools strategically (MP5).
As students work, monitor for students who find a way to scale segment lengths properly but neglect to consider the size of corresponding angles (especially in making a copy of Figure B and D).
Launch
Give students 3 minutes of quiet time to draw and another 3 minutes to share their drawings with a partner, check each other's work, and make revisions. Provide access to their geometry toolkits.
Supports accessibility for: Conceptual processing; Organization
Design Principle(s): Optimize output (for justification)
Student Facing

- Draw a scaled copy of either Figure A or B using a scale factor of 3.
- Draw a scaled copy of either Figure C or D using a scale factor of \(\frac12\).
Student Response
For access, consult one of our IM Certified Partners.
Launch
Give students 3 minutes of quiet time to draw and another 3 minutes to share their drawings with a partner, check each other's work, and make revisions. Provide access to their geometry toolkits.
Representation: Internalize Comprehension. Check in with students after the first 2-3 minutes of work time. Check to make sure students have attended to all parts of the original figures.
Supports accessibility for: Conceptual processing; Organization
Design Principle(s): Optimize output (for justification)
Student Facing

- Draw a scaled copy of either Figure A or B using a scale factor of 3.
- Draw a scaled copy of either Figure C or D using a scale factor of \(\frac12\).

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may think that Figure C cannot be scaled by a factor of \(\frac12\) because some vertices will not land on intersections of grid lines. Clarify that the grid helps us see lengths in whole units but segments we draw on them are not limited to whole units in length.
Activity Synthesis
Invite students to share their strategies of how they used the grid (or other tools) to make sure their drawings were scaled copies. Consider asking questions like:
- How did you know how long to make each side in your scaled copy?
- How did you know how big to make each angle in your scaled copy?
- If you made a mistake while drawing your scaled copy, how could you tell?
Model, prompt, and listen for the language students are using to distinguish between scaled and not scaled figures. Emphasize the usefulness of the grid in drawing and checking right angles, and for drawing and checking lengths of segments. All correct answers will be the same size and shape, but they could be drawn in different positions on the grid.
3.3: Which Operations? (Part 1) (10 minutes)
Activity
The purpose of this activity is to contrast the effects of multiplying side lengths versus adding to side lengths when creating copies of a polygon. To find the corresponding side lengths on a scaled copy, the side lengths of a figure are all multiplied (or divided) by the same number. However, students often mistakenly think that adding or subtracting the same number to all the side lengths will also create a scaled copy. When students recognize that there is a multiplicative relationship between the side lengths rather than an additive one, they are looking for and making use of structure (MP7).
Monitor for students who:
- notice that Diego's copy is no longer a polygon while Jada's still is
- notice that the relationships between side lengths in Diego's copy have changed (e.g., Side 1 is twice as long as Side 2 in the original but is not twice as long as Side 2 in the copy.) while in Jada's copy they have not
- notice that all the corresponding angles have equal measures (i.e., 90 or 270 degrees)
- describe Jada's copy as having all side lengths divided by 3
- describe Jada's copy as having all side lengths a third as long as their original lengths
- describe Jada's copy as having a scale factor of \(\frac13\)
Launch
Give students 2–3 minutes of quiet think time, and then 2 minutes to share their thinking with a partner. See MLR 3 (Clarify, Critique, Correct) and use the strategy "Critique a Partial or Flawed Explanation".
Supports accessibility for: Social-emotional skills; Organization; Language
Student Facing
Diego and Jada want to scale this polygon so the side that corresponds to 15 units in the original is 5 units in the scaled copy.
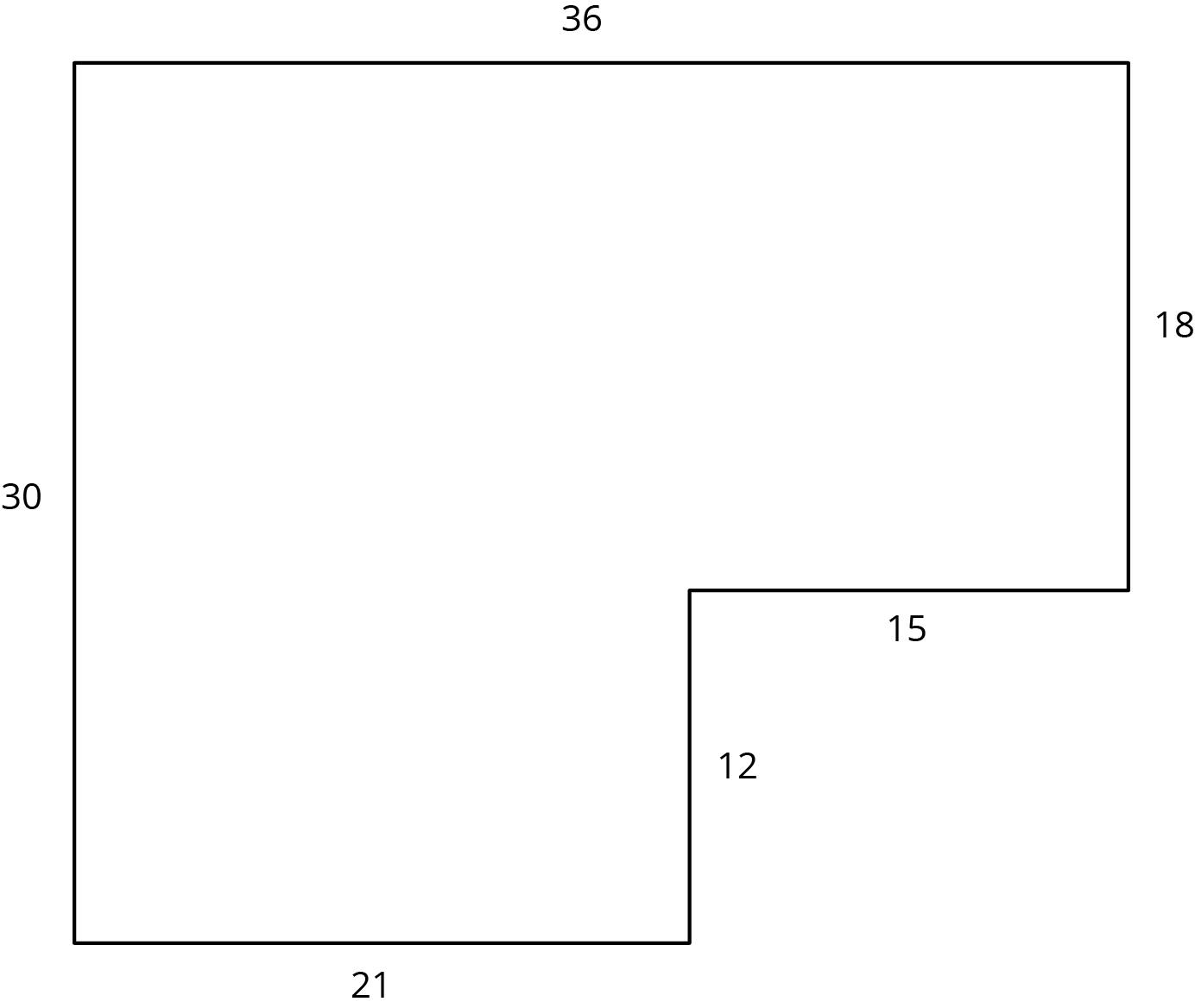
Diego and Jada each use a different operation to find the new side lengths. Here are their finished drawings.
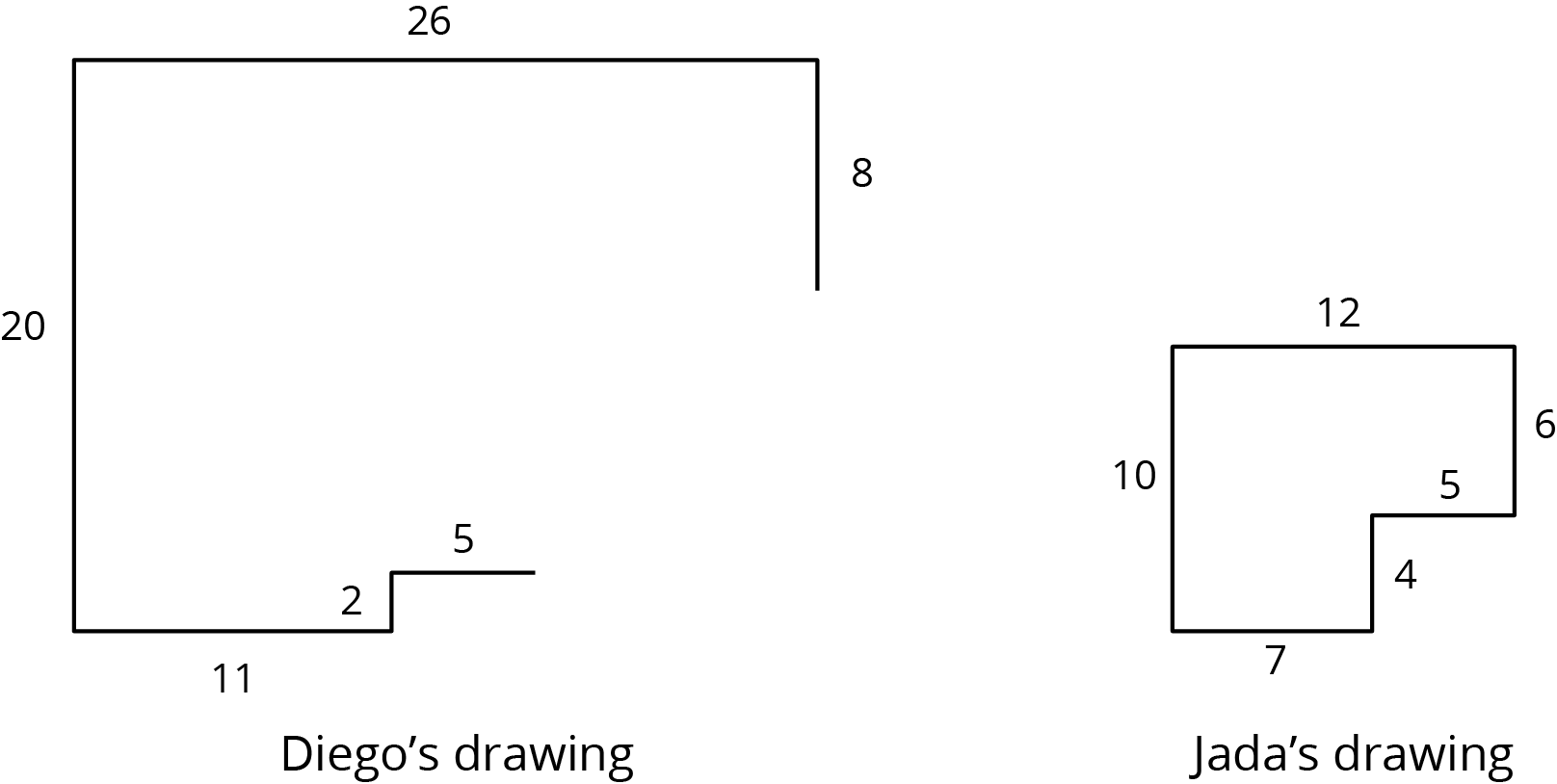
- What operation do you think Diego used to calculate the lengths for his drawing?
- What operation do you think Jada used to calculate the lengths for her drawing?
- Did each method produce a scaled copy of the polygon? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite previously-selected students to share their answers and reasoning. Sequence their explanations from most general to most technical.
Before moving to the next activity, consider asking questions like these:
- What is the scale factor used to create Jada’s drawing? What about for Diego’s drawing? (\(\frac13\) for Jada's; there isn't one for Diego's, because it is not a scaled copy.)
- What can you say about the corresponding angles in Jada and Diego’s drawings? (They are all equal, even though one is a scaled copy and one is not.)
- Subtraction of side lengths does not (usually) produce scaled copies. Do you think addition would work? (Answers vary.)
Note: There are rare cases when adding or subtracting the same length from each side of a polygon (and keeping the angles the same) will produce a scaled copy, namely if all side lengths are the same. If not mentioned by students, it is not important to discuss this at this point.
Representing, writing, and speaking: Math Language Routine 3 Clarify, Critique, Correct. This is the first time Math Language Routine 3 is suggested as a support in this course. In this routine, students are given an incorrect or incomplete piece of mathematical work. This may be in the form of a written statement, drawing, problem-solving steps, or another mathematical representation. Students analyze, reflect on, and improve the written work by correcting errors and clarifying meaning. Typical prompts are: “Is anything unclear?” and/or “Are there any reasoning errors?” The purpose of this routine is to engage students in analyzing mathematical thinking that is not their own, and to solidify their knowledge through communicating about conceptual errors and ambiguities in language.
Design Principle(s): Support sense-making; Optimize output (for reasoning)
How It Happens:
-
Play the role of Diego and present the following statement along with his flawed drawing to the class. “I used a scale factor of minus 10, and Jada used a scale factor of one third. So my drawing is a different kind of scaled copy from Jada’s.”
Ask students, “What steps did Diego take to make the drawing?” and “Did he create a scaled copy? How do you know?” -
Give students 1 minute of quiet think time to analyze the statement, and then 3 minutes to work on improving the statement with a partner.
As pairs discuss, provide these sentence frames for scaffolding: “I believe Diego created the drawing by ___ because ___.”, “Diego created/did not create a scaled copy. I know this because ___.”, “You can’t ___ because ___.” Encourage the listener to ask clarifying questions by referring to the statement and the drawings. Allow each partner to take a turn as the speaker and listener.Listen for students identifying the type of operation used and justification for whether or not a scaled drawing was produced. Have the pairs reach a mutual understanding and agreement on a correct statement about Diego’s drawing.
-
Invite 3 or 4 pairs to present their improved statement to the class, both orally and in writing. . Ask students to listen for order/time transition words (first, next, then, etc.), and any elements of justifications (e.g., First, ___ because ___.).
Here are two sample improved statements:“I subtracted 10 from each side length and Jada used a scale factor of one third. So my drawing is not a scaled copy and Jada’s is. Jada’s is a scaled copy because I know that multiplying—not subtracting—creates a scaled copy. Her drawing created a polygon with no gaps.”
or
“I minused 10 from each side, but I should have realized that in order to scale 15 units in the original down to 5 units in the copy, you have to divide by 3. Jada used a scale factor of one third, which is the same as dividing by 3. My drawing is not a scaled copy and Jada’s is because hers is not a polygon with no gaps, and minusing 10 is not a scale factor.”Call attention to statements that generalize that the method for finding the side lengths of a scaled copy is by multiplying or dividing, not adding or subtracting. Revoice student thoughts with an emphasis on knowing whether or not they created a scaled polygon.
-
Close the conversation on Diego’s drawing, discuss the accuracy of Jada’s scaled copy, and then move on to the next lesson activity.
3.4: Which Operations? (Part 2) (10 minutes)
Activity
In the previous activity, students saw that subtracting the same value from all side lengths of a polygon did not produce a (smaller) scaled copy. This activity makes the case that adding the same value to all lengths also does not produce a (larger) scaled copy, reinforcing the idea that scaling involves multiplication.
This activity gives students a chance to draw a scaled copy without a grid and to use paper as a measuring tool. To create a copy using a scale factor of 2, students need to mark the length of each original segment and transfer it twice onto their drawing surface, reinforcing—in a tactile way—the meaning of scale factor. The angles in the polygon are right angles (and a 270 degree angle in one case) and can be made using the corner of an index card.
Some students may struggle to figure out how to use an index card or a sheet of paper to measure lengths. Before demonstrating, encourage them to think about how a length in the given polygon could be copied onto an index card and used as an increment for measuring. If needed, show how to mark the 4-unit length along the edge of a card and to use the mark to determine the needed lengths for the copy.
Launch
Have students read the task statement and check that they understand which side of the polygon Andre would like to be 8 units long on his drawing. Provide access to index cards, so that students can use it as a measuring tool. Consider not explicitly directing students as to its use to give them a chance to use tools strategically (MP5). Give students 5–6 minutes of quiet work time, and then 2 minutes to share their work with a partner.
Student Facing
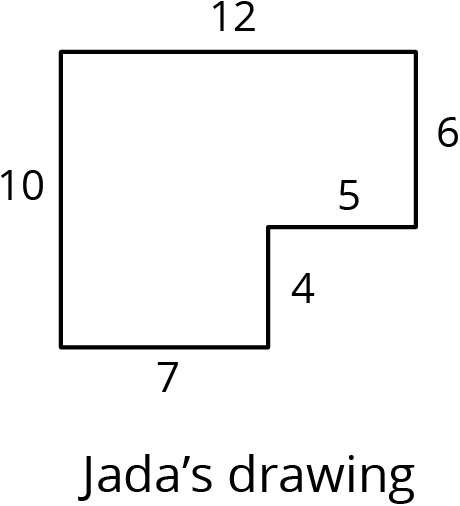
Andre wants to make a scaled copy of Jada's drawing so the side that corresponds to 4 units in Jada’s polygon is 8 units in his scaled copy.
-
Andre says “I wonder if I should add 4 units to the lengths of all of the segments?” What would you say in response to Andre? Explain or show your reasoning.
-
Create the scaled copy that Andre wants. If you get stuck, consider using the edge of an index card or paper to measure the lengths needed to draw the copy.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
The side lengths of Triangle B are all 5 more than the side lengths of Triangle A. Can Triangle B be a scaled copy of Triangle A? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students might not be convinced that making each segment 4 units longer will not work. To show that adding 4 units would work, they might simply redraw the polygon and write side lengths that are 4 units longer, regardless of whether the numbers match the actual lengths. Urge them to check the side lengths by measuring. Tell them (or show, if needed) how the 4-unit length in Jada’s drawing could be used as a measuring unit and added to all sides.
Other students might add 4 units to all sides and manage to make a polygon but changing the angles along the way. If students do so to make the case that the copy will not be scaled, consider sharing their illustrations with the class, as these can help to counter the idea that “scaling involves adding.” If, however, students do this to show that adding 4 units all around does work, address the misconception. Ask them to recall the size of corresponding angles in scaled copies, or remind them that angles in a scaled copy are the same size as their counterparts in the original figure.
Activity Synthesis
The purpose of the activity is to explicitly call out a potential misunderstanding of how scale factors work, emphasizing that scale factors work by multiplying existing side lengths by a common factor, rather than adding a common length to each.
Invite a couple of students to share their explanations or illustrations that adding 4 units to the length of each segment would not work (e.g. the copy is no longer a polygon, or the copy has angles that are different than in the original figure). Then, select a couple of other students to show their scaled copies and share how they created the copies. Consider asking:
- What scale factor did you use to create your copy? Why?
- How did you use an index card (or a sheet of paper) to measure the lengths for the copy?
- How did you measure the angles for the copy?
Speaking: Math Language Routine 7 Compare and Connect. This is the first time Math Language Routine 7 is suggested as a support in this course. In this routine, students are given a problem that can be approached using multiple strategies or representations, and are asked to prepare a visual display of their method. Students then engage in investigating the strategies (by means of a teacher-led gallery walk, partner exchange, group presentation, etc.), compare approaches, and identify correspondences between different representations. A typical discussion prompt is “What is the same and what is different?”, comparing their own strategy to the others. The purpose of this routine is to allow students to make sense of mathematical strategies by identifying, comparing, contrasting, and connecting other approaches to their own, and to develop students’ awareness of the language used through constructive conversations.
Design Principle(s): Maximize meta-awareness
How It Happens:
-
Use this routine to compare and contrast different methods for creating scaled copies of Jada’s drawing. Before selecting students to share a display of their method with the whole class, first give students an opportunity to do this in a group of 3–4.
Invite students to quietly investigate each other’s work. Ask students to consider what is the same and what is different about each display. Invite students to give a step-by-step explanation of their method using this sentence frame: “In order to create the copy, first I…. Next,…. Then, …. Finally,….”. Allow 1–2 minutes for each display and signal when it is time to switch.
-
Next, give each student the opportunity to add detail to their own display for 1-2 minutes. As students work on their displays, circulate the room to identify at least two different methods or two different ways of representing a method. Also look for methods that were only partially successful.
-
Consider selecting 1–2 students to share methods that were only partially successful in producing scaled copies. Then, select a couple of students to share displays of methods that did produce scaled copies.
Draw students’ attention to the approaches used in each drawing (e.g., adding the same value to each side length, not attending to the angles, multiplying by a common factor, not creating a polygon, etc.). Ask students, “Did this approach create a scaled copy? Why or why not?”
-
After the pre-selected students have finished sharing with the whole class, lead a discussion comparing, contrasting, and connecting the different approaches and representations.
In this discussion, demonstrate using the mathematical language “scale factor”, “corresponding”, and “multiplicative” to amplify student language.
Consider using these prompts:
- “How did the scale factor show up in each method?”,
- “Why did the different approaches lead to the same outcome?”,
- “What worked well in _____’s approach/representation? What did not work well?”, and
- “What role does multiplication play in each approach?”
-
Close the discussion by inviting 3 students to revoice the incorrect method for creating a scaled drawing, and then invite 3 different students to revoice the correct method for creating a scaled drawing. Then, transition back to the Lesson Synthesis and Cool Down.
Lesson Synthesis
Lesson Synthesis
- How do we draw a scaled copy of a figure?
- Can we create scaled copies by adding or subtracting the same value from all lengths? Why or why not?
Scaling is a multiplicative process. To draw a scaled copy of a figure, we need to multiply all of the lengths by the scale factor. We saw in the lesson that adding or subtracting the same value to all lengths will not create scaled copies.
3.5: Cool-down - More Scaled Copies (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
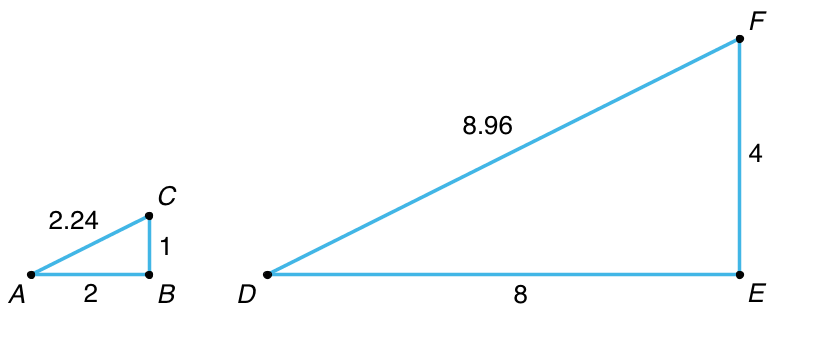
Creating a scaled copy involves multiplying the lengths in the original figure by a scale factor.
For example, to make a scaled copy of triangle \(ABC\) where the base is 8 units, we would use a scale factor of 4. This means multiplying all the side lengths by 4, so in triangle \(DEF\), each side is 4 times as long as the corresponding side in triangle \(ABC\).