Lesson 8
Scale Drawings and Maps
8.1: A Train and a Car (5 minutes)
Warm-up
This warm-up serves two purposes. It refreshes the concept of distance, rate, and time of travel from grade 6, preparing students to use scale drawings to solve speed-related problems. It also allows students to estimate decimal calculations.
Students are likely to approach the question in a few different ways. As students work, notice students using each strategy.
- By finding or estimating the speed of the train in miles per hour and comparing this to the speed of the car
- By finding the distance the car travels in 4 hours and comparing it to the distance the train travels in 4 hours
Launch
Give students 3 minutes of quiet think time. Ask students to calculate the answer mentally and to give a signal when they have an answer and explanation. Follow with a whole-class discussion.
Student Facing
Two cities are 243 miles apart.
-
It takes a train 4 hours to travel between the two cities at a constant speed.
- A car travels between the two cities at a constant speed of 65 miles per hour.
Which is traveling faster, the car or the train? Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share their strategies. Make sure to highlight different strategies, such as calculating the train's speed from the information and calculating how far the car would travel in 4 hours.
Record and display student explanations for all to see. To involve more students in the conversation, consider asking:
- Did anyone solve the problem in a different way?
- Does anyone want to add on to _____’s strategy?
- Do you agree or disagree? Why?
8.2: Driving on I-90 (15 minutes)
Optional activity
Here, students use a scale and a scale drawing to answer a speed-related question. The task involves at least a couple of steps beyond finding the distance of travel and can be approached in several ways. Minimal scaffolding is given here, allowing students to model with mathematics more independently (MP4).
As students work, notice the different approaches they use to find the actual distance and to determine if the driver was speeding. Some likely variations:
- Comparing the speed in miles per minute (calculating the car’s speed in miles per minute and converting the speed limit to miles per minute).
- Comparing the speed in miles per hour (finding the car’s speed in miles per minute and converting it to miles per hour so it can be compared to the speed limit in miles per hour).
- Comparing the time it would take to travel the same distance at two different speeds (the car’s and the limit).
- Comparing the distance traveled in the same amount of time at two different speeds (the car’s and the limit).
Identify students using each method so they can share later.

Launch
Tell students that they will now use a scale drawing (a map) to solve a problem about speed of travel. Survey the class on their familiarity with highway travel and speed limits. If some students are not familiar with speed limits, ask those who are to explain.
Arrange students in groups of 2 and provide access to geometry toolkits. Give students 5 minutes to work on the problem either individually or with their partner.
In the Digital Activity, students have choices about the number of points to plot along the route and whether or not they want to draw segments. Students need to pay attention to the map legend; turning on the grid helps them see that one unit on the grid is equivalent to 0.5 miles.
Supports accessibility for: Social-emotional skills; Conceptual processing
Student Facing
- A driver is traveling at a constant speed on Interstate 90 outside of Chicago. If she traveled from Point A to Point B in 8 minutes, did she obey the speed limit of 55 miles per hour? Explain your reasoning.
- A traffic helicopter flew directly from Point A to Point B in 8 minutes. Did the helicopter travel faster or slower than the driver? Explain or show your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Launch
Tell students that they will now use a scale drawing (a map) to solve a problem about speed of travel. Survey the class on their familiarity with highway travel and speed limits. If some students are not familiar with speed limits, ask those who are to explain.
Arrange students in groups of 2 and provide access to geometry toolkits. Give students 5 minutes to work on the problem either individually or with their partner.
In the Digital Activity, students have choices about the number of points to plot along the route and whether or not they want to draw segments. Students need to pay attention to the map legend; turning on the grid helps them see that one unit on the grid is equivalent to 0.5 miles.
Engagement: Develop Effort and Persistence. Connect a new concept to one with which students have experienced success. For example, draw students attention to the warm-up and remind them how they calculated the speed of the train in miles per hour. Ask students how they can use this method to calculate the speed of driver from Point A to Point B.
Supports accessibility for: Social-emotional skills; Conceptual processing
Student Facing
-
A driver is traveling at a constant speed on Interstate 90 outside Chicago. If she traveled from Point A to Point B in 8 minutes, did she obey the speed limit of 55 miles per hour? Explain your reasoning.
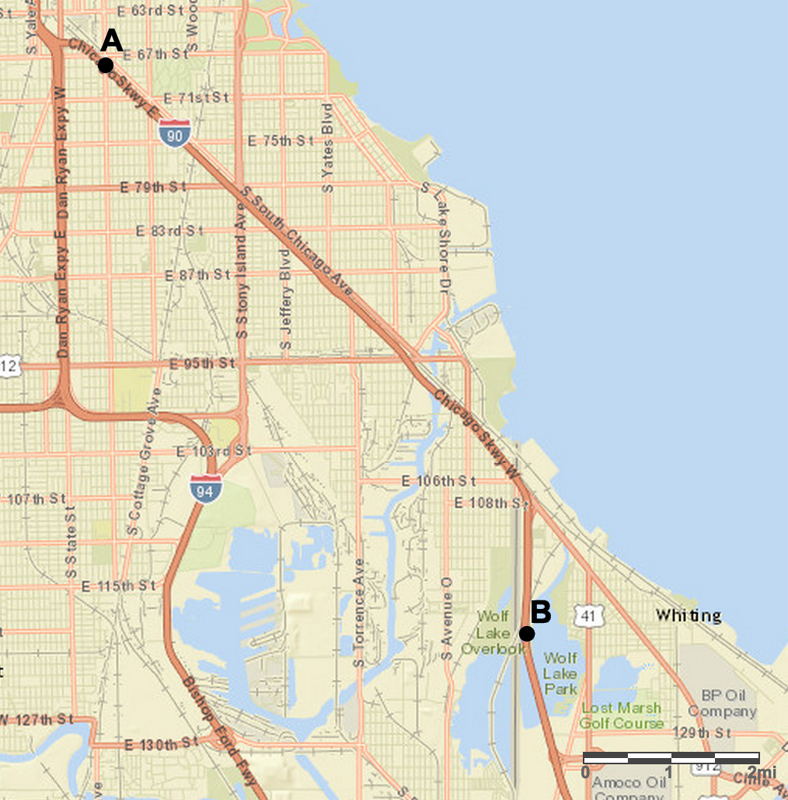
- A traffic helicopter flew directly from Point A to Point B in 8 minutes. Did the helicopter travel faster or slower than the driver? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might not realize that they need to compare two quantities (either two speeds, two distances traveled in the same amount of time, or two durations of travel) in order to answer the question about speeding. Remind them that there are two potential scenarios here: the driver is obeying the speed limit or the driver is not obeying it.
Once students have found the distance between A and B to be about 8.5 miles, they might be inclined to divide 55 by 8.5 simply because 55 is a larger number. Using double number lines or a table to show the relationship between miles traveled and number of hours might be helpful, as might using friendlier examples of distances (e.g., “How long would it take to travel 110 miles? 11 miles?”).
Activity Synthesis
Ask students to indicate whether they believe the driver was speeding or not. Invite students who approached the task in different ways to share, highlighting methods that focus on:
- Calculating or estimating the speed the driver is traveling (in miles per minute or miles per hour)
- Finding how long it would take to make the trip at the speed limit
- Finding how far the driver would travel in 8 minutes going at the speed limit
Display their work or record or summarize it for all to see.
Ask students if they thought any method seems more efficient than others and why. Highlight that all the methods involved finding the distance traveled, and that the scale drawing and scale enabled us to find that distance.
One method for solving this problem which avoids the decimals that approximate fractional quantities is to observe that 55 miles per hour is the same as 55 miles in 60 minutes, so that is less than one mile per minute. So it will take more than 8.5 minutes to travel 8.5 miles at 55 miles per hour, and the driver must have been speeding.
8.3: Biking through Kansas (10 minutes)
Optional activity
In the previous activity, students were given a map with a scale and the amount of time it took to get from one place to another. They used this to estimate the speed of the trip. In this activity, students work with the speed and a map with scale to find the amount of time a trip will take.
The main strategy to expect is to measure the distance between the two locations on the map and use the scale to convert this to the distance between the actual cities. Then students can calculate how long it will take at 15 mph.
Launch
Tell students that they will now use a scale drawing (a map) to solve a different problem about travel, this time focusing on how long it will take. Ask students what is the farthest they have ever biked. How long did it take? Do they know someone who has biked farther or for longer? If so, how far and how long?
Keep students in the same groups. Give students 4–5 minutes of quiet work time followed by partner and whole-class discussion.
Student Facing
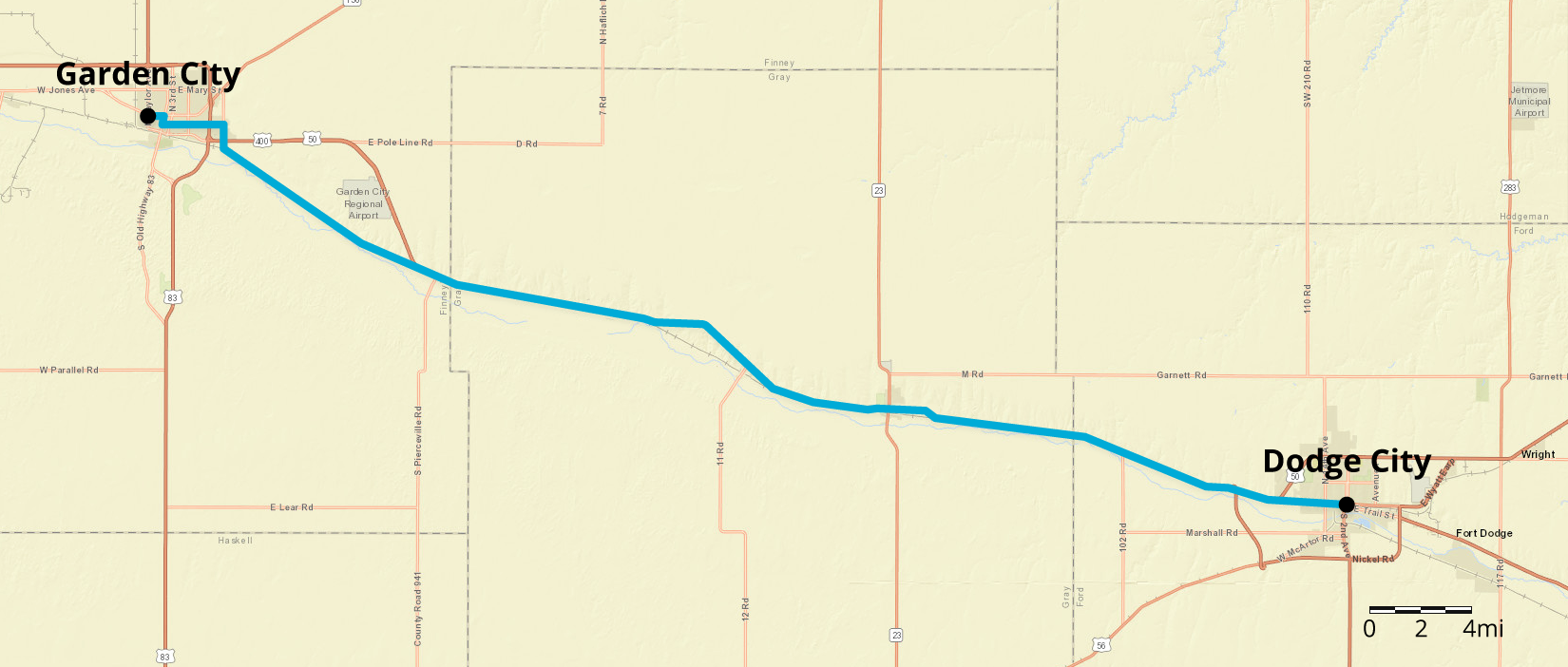
A cyclist rides at a constant speed of 15 miles per hour. At this speed, about how long would it take the cyclist to ride from Garden City to Dodge City, Kansas?

Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Jada finds a map that says, “Note: This map is not to scale.” What do you think this means? Why is this information important?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
The road from Garden City to Dodge City has many twists and bends. Students may not be sure how to treat these. Tell them to make their best estimate. Measuring many small segments of the road will have the advantage that those short segments are straight but it is time consuming. A good estimate will be sufficient here.
Activity Synthesis
First, have students compare answers with a partner and discuss their reasoning until they reach an agreement.
Next, invite students to share how they estimated the distance between the two cities (and how long it takes the cyclist to travel this distance). Ask students to consider the different distances students estimated the trip to be. What are some reasons for the differences? Possible explanations include:
- Measurement error
- The road is not straight and so needs to be approximated
- For students who lay out the scale over and over again to cover the distance, it is difficult to estimate the fraction of the scale at the last step
Because of these different sources of inaccuracy, reporting the distance as 50 miles is reasonable; reporting it as 52 miles would require a lot of time and measurements; and reporting it as 51.6 miles is not reasonable with the given scale and map.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
A map with a scale helps estimate the distance between two places by measuring the distance on the map and using the scale to find the actual distance. Once the distance between two places is known:
- If we know how long the trip takes, we can calculate the speed by finding the quotient of the distance and the time.
- If we know the speed, we can calculate how long the trip takes by finding the quotient of the distance and the speed.
In both cases, care has to be taken regarding units. For example, if a
130-mile trip at a constant speed takes two hours, then the speed is 65 miles per hour, because \(130 \div 2 = 65\). A 35-mile trip at 70 miles per hour takes \(\frac{1}{2}\) hour, because \(35 \div 70 = \frac{1}{2}\).
8.4: Cool-down - Walking Around the Botanical Garden (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Maps with scales are useful for making calculations involving speed, time, and distance. Here is a map of part of Alabama.
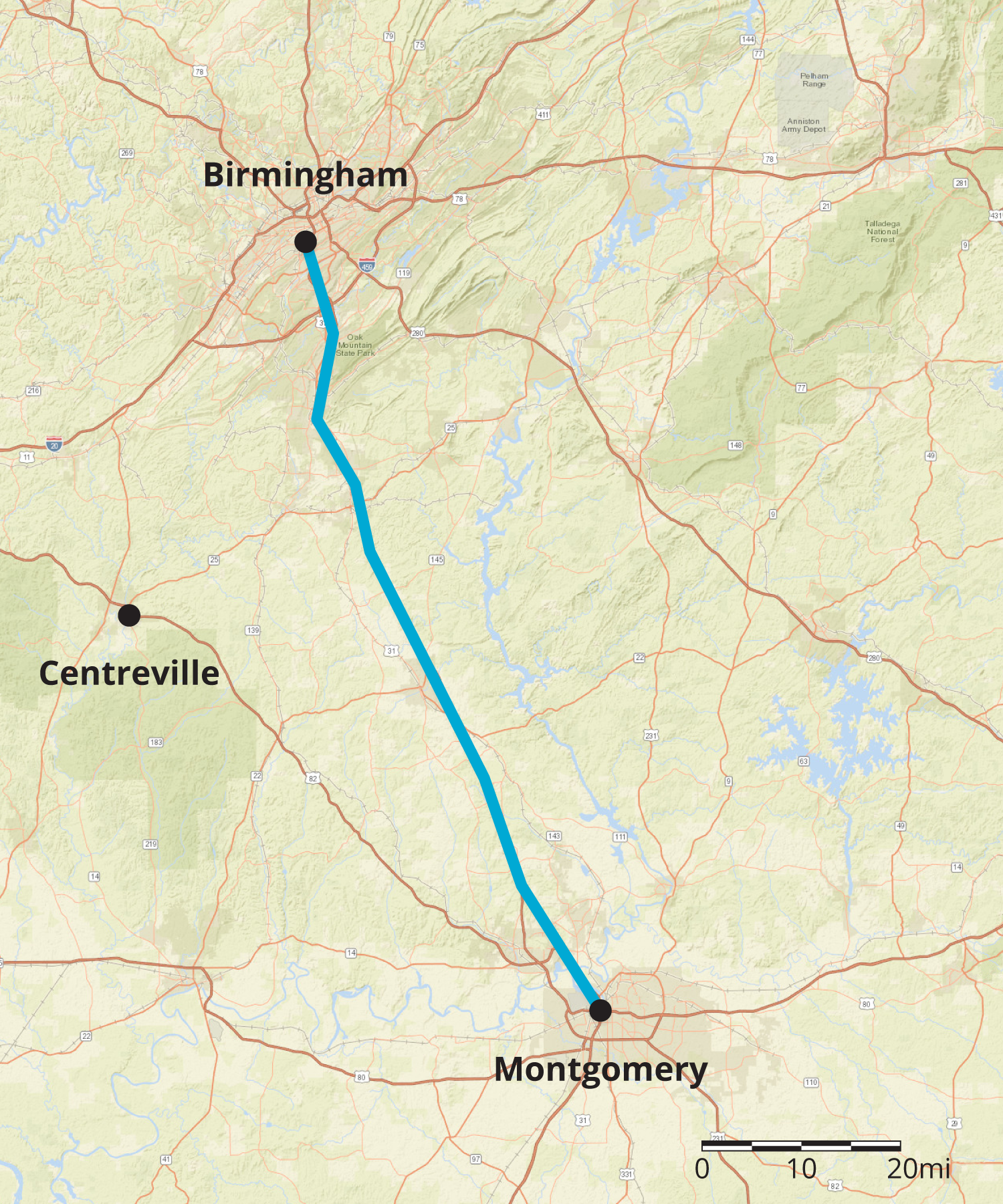
Suppose it takes a car 1 hour and 30 minutes to travel at constant speed from Birmingham to Montgomery. How fast is the car traveling?
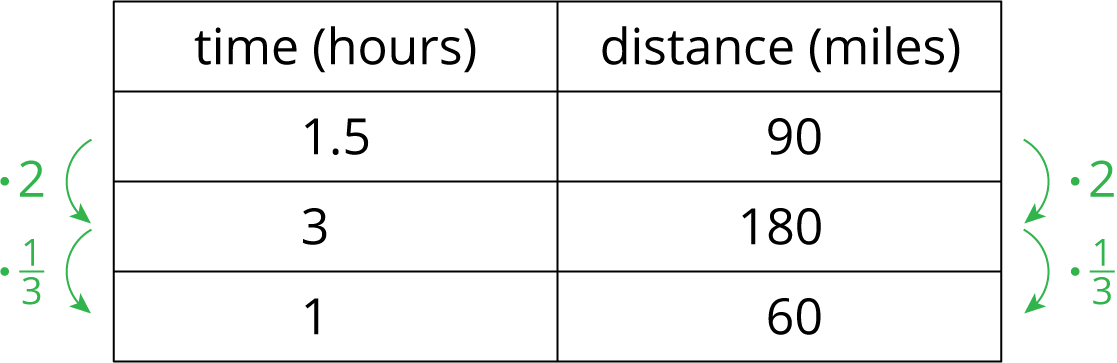
To make an estimate, we need to know about how far it is from Birmingham to Montgomery. The scale of the map represents 20 miles, so we can estimate the distance between these cities is about 90 miles.
Since 90 miles in 1.5 hours is the same speed as 180 miles in 3 hours, the car is traveling about 60 miles per hour.
Suppose a car is traveling at a constant speed of 60 miles per hour from Montgomery to Centreville. How long will it take the car to make the trip? Using the scale, we can estimate that it is about 70 miles. Since 60 miles per hour is the same as 1 mile per minute, it will take the car about 70 minutes (or 1 hour and 10 minutes) to make this trip.