Lesson 2

Corresponding Parts and Scale Factors

This lesson develops the vocabulary for talking about scaling and scaled copies more precisely (MP6), and identifying the structures in common between two figures (MP7).

Specifically, students learn to use the term corresponding to refer to a pair of points, segments, or angles in two figures that are scaled copies. Students also begin to describe the numerical relationship between the corresponding lengths in two figures using a scale factor. They see that when two figures are scaled copies of one another, the same scale factor relates their corresponding lengths. They practice identifying scale factors.

A look at the angles of scaled copies also begins here. Students use tracing paper to trace and compare angles in an original figure and its copies. They observe that in scaled copies the measures of corresponding angles are equal.

Comprehend the phrase “scale factor” and explain (orally) how it relates corresponding lengths of a figure and its scaled copy.
Explain (orally) what it means to say one part in a figure “corresponds” to a part in another figure.
Identify and describe (orally and in writing) corresponding points, corresponding segments, or corresponding angles in a pair of figures.

Let’s describe features of scaled copies.

Geometry toolkits

Prepare to display the images of the railroad crossing sign for the Corresponding Parts activity. Make sure students have access to their geometry toolkits, especially tracing paper and graph paper.

I can describe what the scale factor has to do with a figure and its scaled copy.
In a pair of figures, I can identify corresponding points, corresponding segments, and corresponding angles.

Building On

Addressing

7.G.A.1

Building Towards

7.RP.A.2

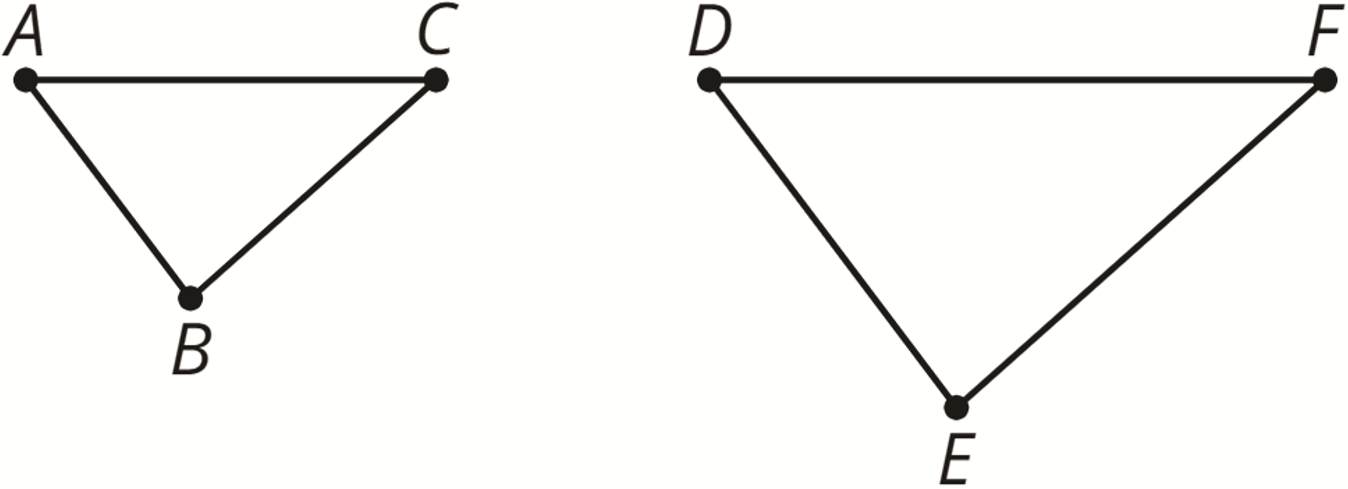
corresponding

When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).
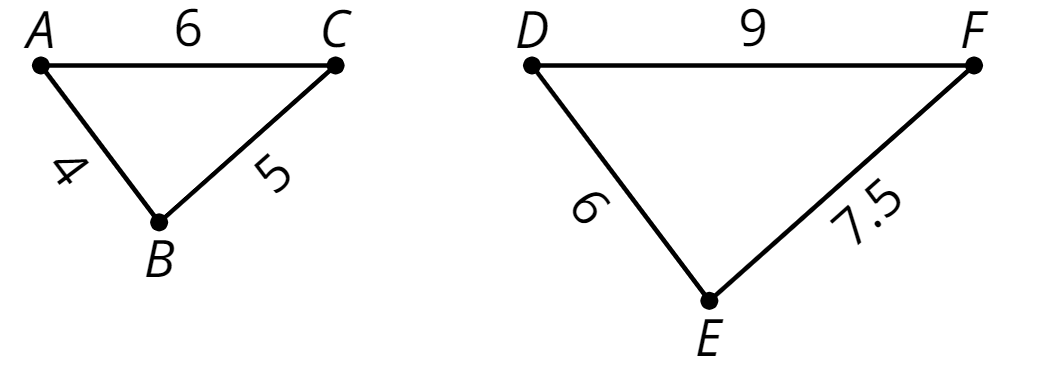
scale factor

To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

In this example, the scale factor is 1.5, because \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).