Lesson 10
The Distributive Property, Part 2
Problem 1
Here is a rectangle.
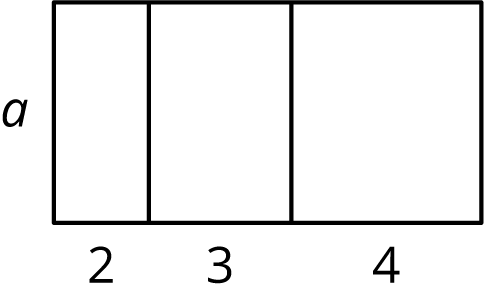
- Explain why the area of the large rectangle is \(2a + 3a + 4a\).
- Explain why the area of the large rectangle is \((2+3+4)a\).
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Is the area of the shaded rectangle \(6(2-m)\) or \(6(m-2)\)?
Explain how you know.

Solution
For access, consult one of our IM Certified Partners.
Problem 3
Choose the expressions that do not represent the total area of the rectangle. Select all that apply.
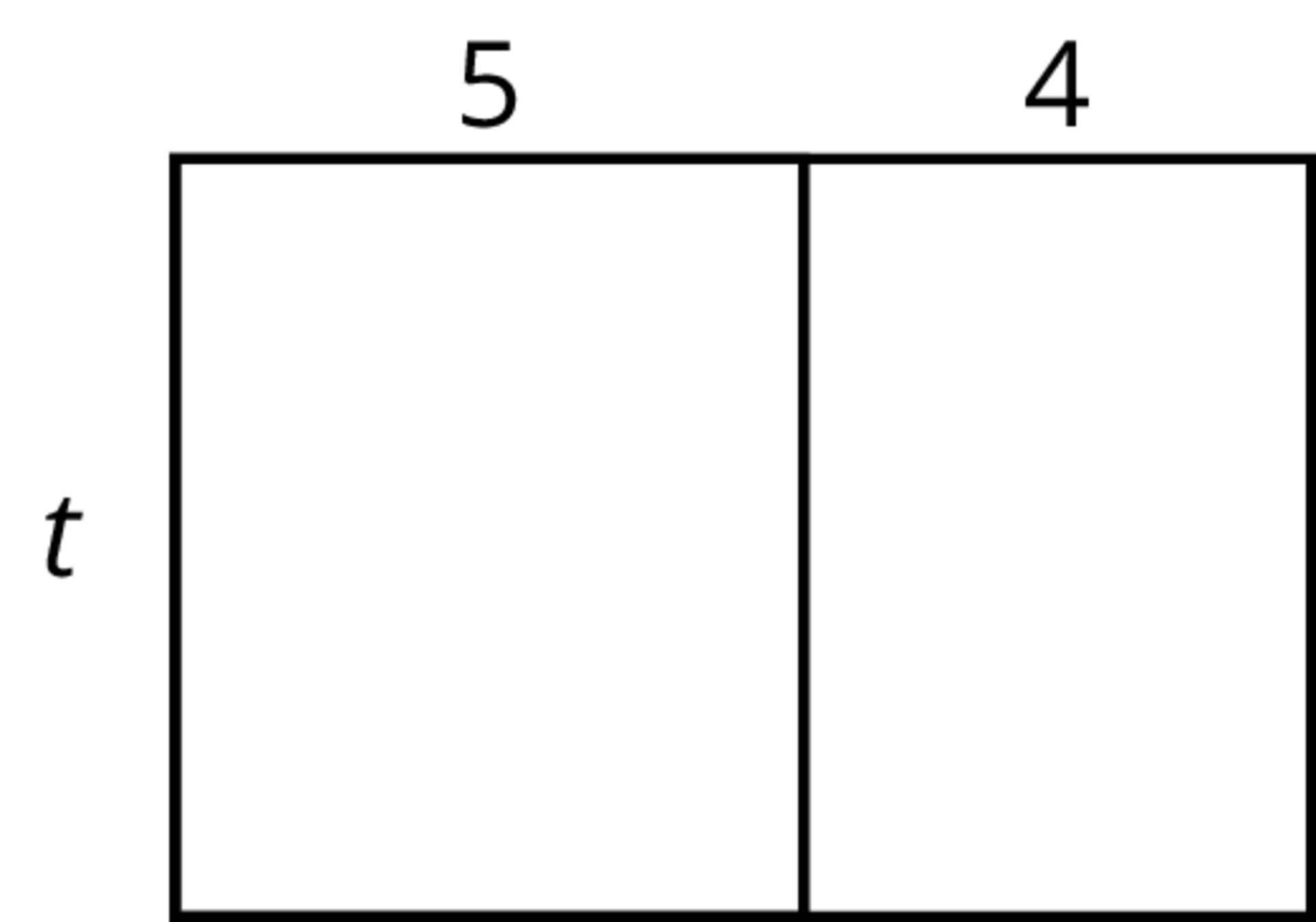
\(5t + 4t\)
\(t + 5 + 4\)
\(9t\)
\(4 \boldcdot 5 \boldcdot t\)
\(t(5+4)\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Evaluate each expression mentally.
- \(35\boldcdot 91-35\boldcdot 89\)
- \(22\boldcdot 87+22\boldcdot 13\)
- \(\frac{9}{11}\boldcdot \frac{7}{10}-\frac{9}{11}\boldcdot \frac{3}{10}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 9.)Problem 5
Select all the expressions that are equivalent to \(4b\).
\(b+b+b+b\)
\(b+4\)
\(2b+2b\)
\(b \boldcdot b \boldcdot b \boldcdot b\)
\(b \div \frac{1}{4}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 8.)Problem 6
Solve each equation. Show your reasoning.
\(111=14a\)
\(13.65 = b + 4.88\)
\(c+ \frac{1}{3} = 5\frac{1}{8}\)
\(\frac{2}{5} d = \frac{17}{4}\)
\(5.16 = 4e\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 4.)Problem 7
Andre ran \(5\frac{1}{2}\) laps of a track in 8 minutes at a constant speed. It took Andre \(x\) minutes to run each lap. Select all the equations that represent this situation.
\(\left(5\frac{1}{2}\right)x = 8\)
\(5 \frac{1}{2} + x = 8\)
\(5 \frac{1}{2} - x = 8\)
\(5 \frac{1}{2} \div x = 8\)
\(x = 8 \div \left(5\frac{1}{2}\right)\)
\(x = \left(5\frac{1}{2}\right) \div 8\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 2.)