Lesson 12
Meaning of Exponents
12.1: Notice and Wonder: Dots and Lines (5 minutes)
Warm-up
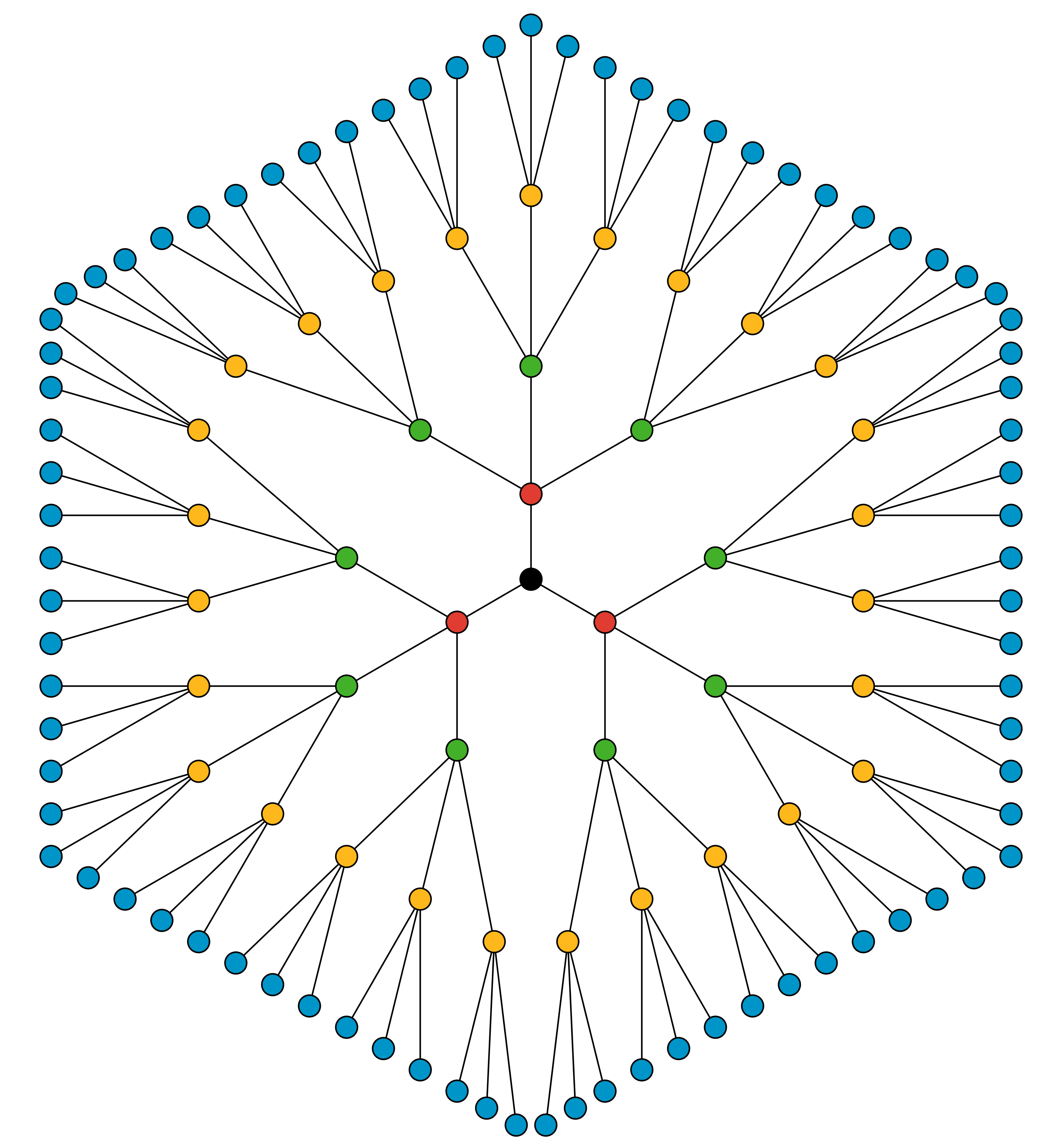
The purpose of this warm-up is to give students an opportunity to look for multiplication patterns in an image. While there are many things students may notice and wonder, the focus of the whole-group discussion should be the fact that each dot branches out to three more dots of a different color. These connections mean we have repeatedly growing groups of 3, so we can multiply by 3 to find the number of dots and lines at various stages. In the image, there are many other patterns students may see with the dots, lines and dot colors. Record or otherwise validate their observations, but don’t dwell too long here.
Launch
Arrange students in groups of 2. Tell students that they will look at a picture, and their job is to think of at least one thing they notice and at least one thing they wonder about the picture. Display the problem for all to see and give 1 minute of quiet think time. Ask students to give a signal when they have noticed or wondered about something. Tell them to share the things they noticed and wondered with a partner.
Supports accessibility for: Memory; Organization
Student Facing
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may try to count the dots in the two outer levels. To encourage students to use the patterns in the image, ask them if there is an easier way they could use their count from the level before to determine the next one.
Activity Synthesis
After giving students a chance to share what they noticed and wondered with a partner, ask a few students to share with the whole group. Record and display their responses for all to see. After each response, ask the class if they agree or disagree.
12.2: The Genie’s Offer (20 minutes)
Activity
The purpose of this task is to show a simple context where exponent notation is naturally useful. The task lends itself to connecting repeated calculations with an expression involving exponents (MP8). This motivates creating a shorthand notation that can be used to answer the questions.
Launch
You find a brass bottle that looks really old. When you rub some dirt off the bottle,a genie appears! The genie offers you a reward. You must choose one:
- Take $50,000; or
- Take a magical $1 coin. The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.
Ask students to close their books or devices. Display the scenario above for all to see, or explain it verbally. Ask students, “What do you notice? What do you wonder?” It is natural to wonder which is the better option. Poll the class and record the results. If possible, show the first few screens from the applet at ggbm.at/hvJbDbjg to help students see how the coins double each day, keeping the “Count” hidden. Use the Play and Pause buttons in the lower left corner of the screen. If it cannot be projected for all to see, ask students to describe what the first four days of the second offer would look like. Draw their descriptions for all to see.
Distribute scientific calculators to students or be ready to display desmos.com/scientific. Follow with 5 minutes of quiet work time for students to complete the first two questions and then pause for discussion. Draw students' attention to the third question. Ask them, “How would you use the calculator to figure this out?” After a minute of quiet think time, solicit responses. Tell students how to calculate with exponents on the calculator and make the point that exponent notation is much more convenient for calculation and communication than writing out all the repeated factors. Give students 5 minutes to complete the last two questions, followed by whole-class discussion.
Supports accessibility for: Language; Conceptual processing
Student Facing
You find a brass bottle that looks really old. When you rub some dirt off of the bottle, a genie appears! The genie offers you a reward. You must choose one:
- $50,000; or
- A magical $1 coin. The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.
- The number of coins on the third day will be \(2 \boldcdot 2 \boldcdot 2\). Write an equivalent expression using exponents.
- What do \(2^5\) and \(2^6\) represent in this situation? Evaluate \(2^5\) and \(2^6\) without a calculator.
- How many days would it take for the number of magical coins to exceed $50,000?
- Will the value of the magical coins exceed a million dollars within the 28 days? Explain or show your reasoning.
Explore the applet. (Why do you think it stops?)
Student Response
For access, consult one of our IM Certified Partners.
Launch
You find a brass bottle that looks really old. When you rub some dirt off the bottle, a genie appears! The genie offers you a reward. You must choose one:
- Take $50,000; or
- Take a magical $1 coin. The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.
Ask students to close their books or devices. Display the scenario above for all to see, or explain it verbally. Ask students, “What do you notice? What do you wonder?” It is natural to wonder which is the better option. Poll the class and record the results. If possible, show the first few screens from the applet at ggbm.at/hvJbDbjg to help students see how the coins double each day, keeping the “Count” hidden. Use the Play and Pause buttons in the lower left corner of the screen. If it cannot be projected for all to see, ask students to describe what the first four days of the second offer would look like. Draw their descriptions for all to see.
Distribute scientific calculators to students or be ready to display desmos.com/scientific. Follow with 5 minutes of quiet work time for students to complete the first two questions and then pause for discussion. Draw students' attention to the third question. Ask them, “How would you use the calculator to figure this out?” After a minute of quiet think time, solicit responses. Tell students how to calculate with exponents on the calculator and make the point that exponent notation is much more convenient for calculation and communication than writing out all the repeated factors. Give students 5 minutes to complete the last two questions, followed by whole-class discussion.
Supports accessibility for: Language; Conceptual processing
Student Facing
You find a brass bottle that looks really old. When you rub some dirt off of the bottle, a genie appears! The genie offers you a reward. You must choose one:
$50,000 or a magical $1 coin.
The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.
- The number of coins on the third day will be \(2 \boldcdot 2 \boldcdot 2\). Write an equivalent expression using exponents.
-
What do \(2^5\) and \(2^6\) represent in this situation? Evaluate \(2^5\) and \(2^6\) without a calculator. Pause for discussion.
- How many days would it take for the number of magical coins to exceed $50,000?
- Will the value of the magical coins exceed a million dollars within the 28 days? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A scientist is growing a colony of bacteria in a petri dish. She knows that the bacteria are growing and that the number of bacteria doubles every hour.
When she leaves the lab at 5 p.m., there are 100 bacteria in the dish. When she comes back the next morning at 9 a.m., the dish is completely full of bacteria. At what time was the dish half full?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might evaluate \(2^5\) as \(2\boldcdot 5\). If this happens, have them make a table showing the number of coins accumulated each day. It will soon be apparent that many more than 10 coins will be accumulated after 5 days.
Activity Synthesis
The goal of the discussion is for students to connect the idea of multiplying \(n\) factors of 2 to get the expression \(2^n\). This notation is convenient for communicating and computing when repeated multiplication is involved. Here are some questions for discussion:
- “How did you know what \(2^5\) represents? How did you evaluate it?”
- “How many times greater is \(2^8\) than \(2^7\)? Could you answer this without evaluating both expressions?”
- “Why does writing expressions with exponents make them easier to work with and understand?”
- “How did you organize your work to answer questions 3 and 4?”
- “Use your calculator to find how much money you would get at the end of 28 days. Does it surprise you?”
Design Principle(s): Optimize output (for explanation)
12.3: Make 81 (10 minutes)
Activity
In this activity, students apply the meaning of exponents to practice writing and evaluating exponential expressions. Students gain experience experimenting with equivalent numerical expressions and engage in looking for structure (MP7) when they replace a portion of an expression with something equivalent to it.
Launch
An exponent is used to indicate multiplying a number by itself. For example, \(2^4\) means \(2 \boldcdot 2 \boldcdot 2 \boldcdot 2\), so \(2^4\) equals 16.
There are different ways to say \(2^4\). You can say “two raised to the power of four” or “two to the fourth power” or just “two to the fourth.”
Give students 5 minutes of quiet work time, followed by whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Optimize output (for justification); Maximize meta-awareness
Student Facing
-
Here are some expressions. All but one of them equals 16. Find the one that is not equal to 16 and explain how you know.
\(2^3\boldcdot 2\)
\(4^2\)
\(\frac{2^5}{2}\)
\(8^2\)
-
Write three expressions containing exponents so that each expression equals 81.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
In expressions with multiplication and exponents, students might parse the expression incorrectly, or apply the order of operations incorrectly. For example, they might interpret \(2^3\boldcdot 2\) as \(4^3\) instead of 2 multiplied by itself 4 times. Students might also multiply the base and exponent, \(9^2=18\) instead of \(9^2 =81\).
To help students overcome these misconceptions, ask students to rewrite the expressions without exponents. For example, \(2^3\boldcdot2=2\boldcdot2\boldcdot2\boldcdot2=16\). Once students have demonstrated conceptual understanding of exponents and why exponents come before multiplication in the order of operations, students will be able to evaluate without rewriting expressions.
Activity Synthesis
The purpose of the discussion is to help students consider that, just as they did with addition, subtraction, multiplication, and division, they can express numbers in multiple ways using exponents. After reviewing the first question and addressing any misconceptions, ask students to share some of their expressions for the second question. Look for expressions that go beyond the more obvious choices and that involve other operations. If no students found more creative expressions, challenge them to come up with one more expression that involves an exponent and another operation. Ask students to share with the class what they came up with and have other students confirm that they evaluate to 81.
You might also ask students to write expressions that do not equal 81, but look like the error in question 1.
Lesson Synthesis
Lesson Synthesis
Ask students to think back to the dot pattern they saw at the beginning of the lesson and address some of the things they may have wondered:
- “Can we write an expression for the number of dots in the outer layer?” (3 with an exponent that is the number of the layer)
- “Based on that expression, how many dots were in the layer before? In the next layer? In the one after that? What part of the expression would change as we move from layer to layer? In what way would it change?” (The exponent changes, it increases by one for each higher layer and decreases by one for each lower layer)
- “What would happen if there were only 2 dots connected to each one? 4 dots? What part of the expression would change?” (The number that is being repeatedly multiplied would change.)
- “How can we use what we know about one layer to find out how many dots there are in another layer?” (Multiply or divide by 3 the same number of times as the layers moved. Notice incidentally that \(a^n=a\boldcdot a^{n-1}\) but without using exponential notation.)
12.4: Cool-down - More 3's (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
When we write an expression like \(2^n\), we call \(n\) the exponent.
If \(n\) is a positive whole number, it tells how many factors of 2 we should multiply to find the value of the expression. For example, \(2^1=2\), and \(2^5=2 \boldcdot 2 \boldcdot 2 \boldcdot 2 \boldcdot 2\).
There are different ways to say \(2^5\). We can say “two raised to the power of five” or “two to the fifth power” or just “two to the fifth.”