Lesson 10

The Distributive Property, Part 2

Let's use rectangles to understand the distributive property with variables.

10.1: Possible Areas

  1. A rectangle has a width of 4 units and a length of \(m\) units. Write an expression for the area of this rectangle.

  2. What is the area of the rectangle if \(m\) is:

    3 units?

    2.2 units?

    \(\frac15\) unit?

  3. Could the area of this rectangle be 11 square units? Why or why not?

10.2: Partitioned Rectangles When Lengths are Unknown

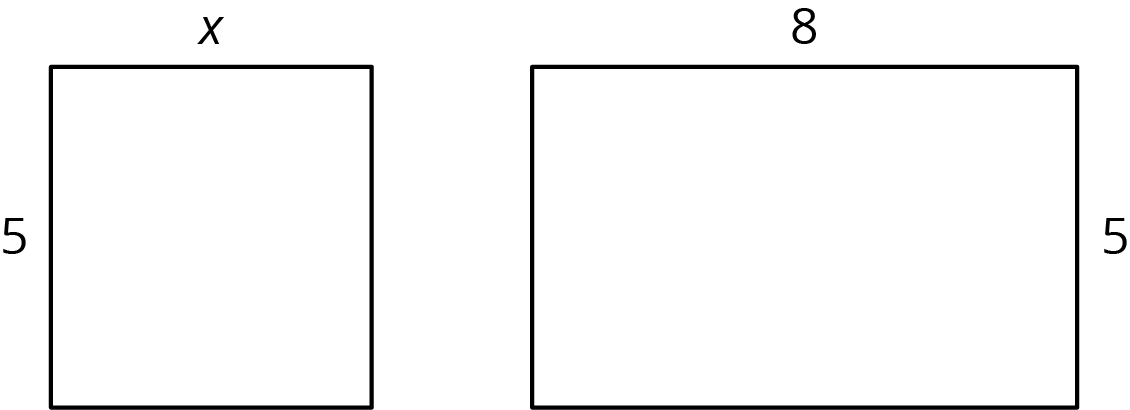
  1. Here are two rectangles. The length and width of one rectangle are 8 and 5. The width of the other rectangle is 5, but its length is unknown so we labeled it \(x\).

    Write an expression for the sum of the areas of the two rectangles.

    Two rectangles. The first rectangle has a height of 5 and width of x. The second rectangle has a height of 5 and width of 8.

  2. The two rectangles can be composed into one larger rectangle as shown.

    What are the width and length of the new, large rectangle?

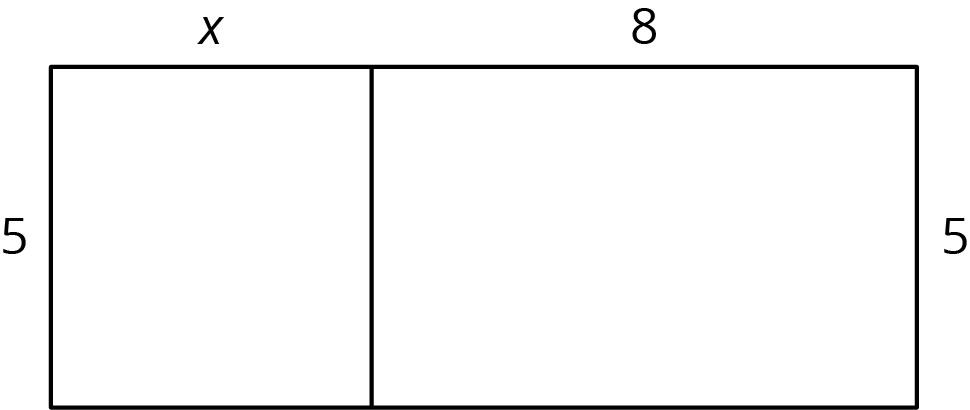
    Rectangle diagram. The first rectangle has a height of 5 and width of x. Attached is a second rectangle with the same height and width of 8.
  3. Write an expression for the total area of the large rectangle as the product of its width and its length.

10.3: Areas of Partitioned Rectangles

For each rectangle, write expressions for the length and width and two expressions for the total area. Record them in the table. Check your expressions in each row with your group and discuss any disagreements.

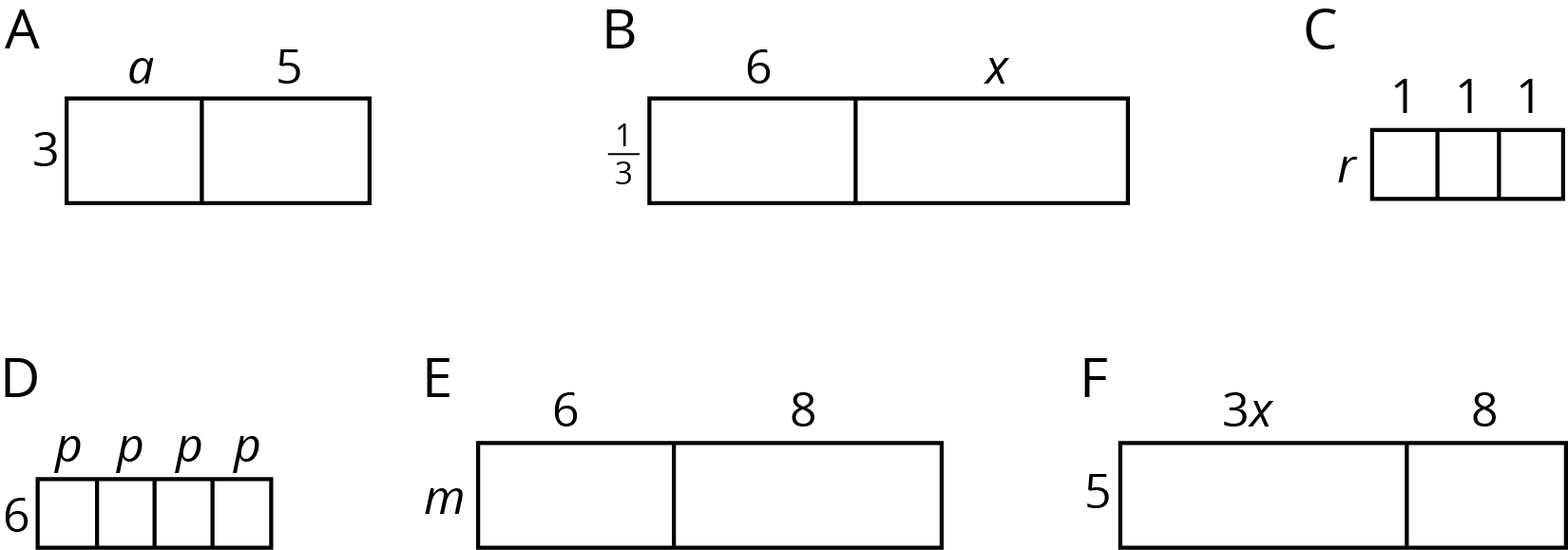
Six different sized rectangles labeled A, B, C, D, E, and F.

 

rectangle   width     length   area as a product of
width times length		 area as a sum of the areas
of the smaller rectangles

A

B

C

D

E

F

 



Here is an area diagram of a rectangle.

Area diagram of a rectangle partition into 4 smaller rectangle.
  1. Find the lengths \(w\), \(x\), \(y\), and \(z\), and the area \(A\). All values are whole numbers.
  2. Can you find another set of lengths that will work? How many possibilities are there?

Summary

Here is a rectangle composed of two smaller rectangles A and B.

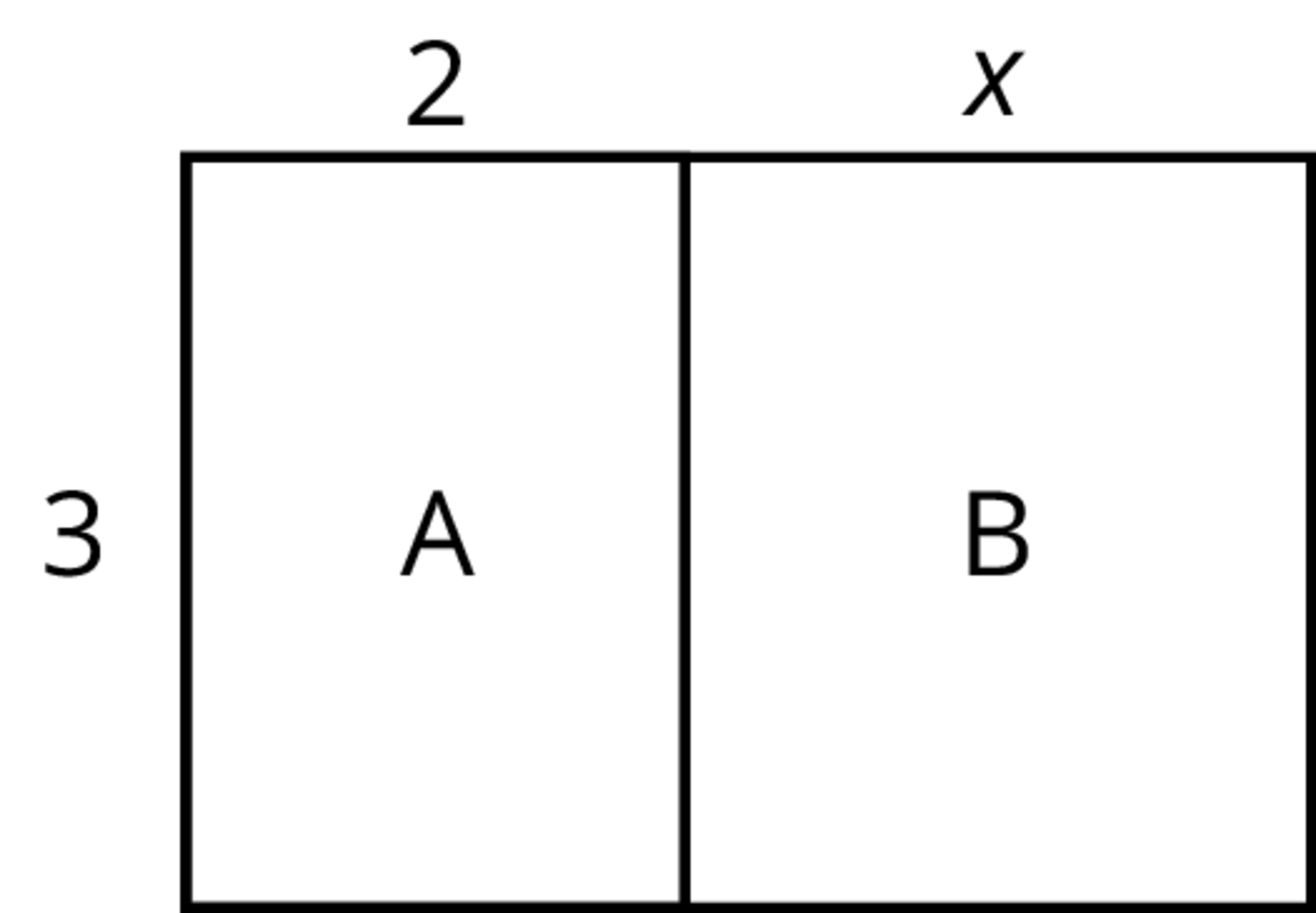
A partitioned rectangle.

Based on the drawing, we can make several observations about the area of the rectangle:

  • One side length of the large rectangle is 3 and the other is \(2+x\), so its area is \(3(2+x)\).
  • Since the large rectangle can be decomposed into two smaller rectangles, A and B, with no overlap, the area of the large rectangle is also the sum of the areas of rectangles A and B: \(3(2) + 3(x)\) or \(6+3x\).
  • Since both expressions represent the area of the large rectangle, they are equivalent to each other. \(3(2+x)\) is equivalent to \(6 + 3x\).

We can see that multiplying 3 by the sum \(2+x\) is equivalent to multiplying 3 by 2 and then 3 by \(x\) and adding the two products. This relationship is an example of the distributive property.

\(\displaystyle 3(2+x) = 3 \boldcdot 2 + 3 \boldcdot x\)

Video Summary

Video VLS G6U6V3 Writing Equivalent Expressions (Lessons 8–11) available at https://player.vimeo.com/video/513058816.

Glossary Entries

  • equivalent expressions

    Equivalent expressions are always equal to each other. If the expressions have variables, they are equal whenever the same value is used for the variable in each expression.

    For example, \(3x+4x\) is equivalent to \(5x+2x\). No matter what value we use for \(x\), these expressions are always equal. When \(x\) is 3, both expressions equal 21. When \(x\) is 10, both expressions equal 70.

  • term

    A term is a part of an expression. It can be a single number, a variable, or a number and a variable that are multiplied together. For example, the expression \(5x + 18\) has two terms. The first term is \(5x\) and the second term is 18.