Lesson 9
The Distributive Property, Part 1
9.1: Number Talk: Ways to Multiply (5 minutes)
Warm-up
Students perform mental calculations by applying strategies involving the distributive property.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all problems displayed throughout the talk. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find each product mentally.
\(5 \boldcdot 102\)
\(5 \boldcdot 98\)
\(5 \boldcdot 999\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Once students have had a chance to share a few different ways of reasoning about this product, focus on explanations using the distributive property like \(5 \boldcdot 98 = 5 \boldcdot (90 + 8)\) or \(5 \boldcdot (100 - 2)\), then writing out the two products from distributing. Remind students of the distributive property, and let them know they will spend the next few lessons working with it.
Design Principle(s): Optimize output (for explanation)
9.2: Ways to Represent Area of a Rectangle (15 minutes)
Activity
The purpose of this activity is to remind students of rectangle diagrams they worked with in a previous unit to represent multiplication. It is also to introduce the convention that for example the expression \(6 \boldcdot 3 + 2\) equals 20. If we want the sum to be carried out before the product, we would need to use parentheses like \(6 \boldcdot (3+2)\).
Launch
Allow students 10 minutes of quiet work time, followed by a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Student Facing
-
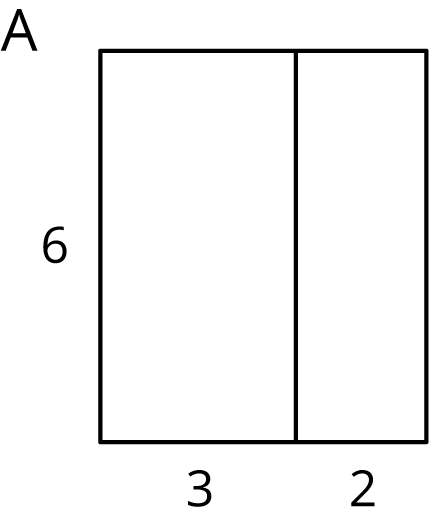
Select all the expressions that represent the area of the large, outer rectangle in figure A. Explain your reasoning.
- \(6 + 3 + 2\)
- \(6 \boldcdot 3 + 6 \boldcdot 2\)
- \(6 \boldcdot 3 + 2\)
- \(6 \boldcdot 5\)
- \(6 (3+2)\)
- \(6 \boldcdot 3 \boldcdot 2\)
-
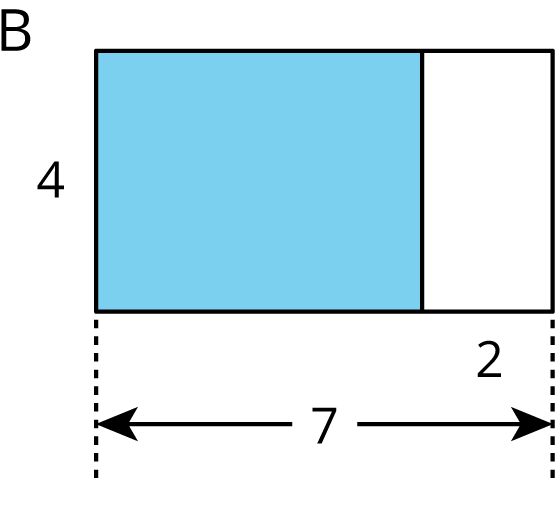
Select all the expressions that represent the area of the shaded rectangle on the left side of figure B. Explain your reasoning.
- \(4 \boldcdot 7 + 4 \boldcdot 2\)
- \(4 \boldcdot 7 \boldcdot 2\)
- \(4 \boldcdot 5\)
- \(4 \boldcdot 7 - 4 \boldcdot 2\)
- \(4(7-2)\)
- \(4(7+2)\)
- \(4 \boldcdot 2 - 4 \boldcdot 7\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Students may conclude that \(6 \boldcdot 3 + 2\) represents the area of the rectangle. This is a good opportunity to introduce a convention. When we have multiplication and addition in the same expression, it is the convention that the multiplication is done first. So \(6 \boldcdot 3 + 2\) equals \(18 + 2\), or 20, so it doesn’t represent the area of the rectangle, which we know to be 30 square units. If you want the addition to be done first, you need to use parentheses. Therefore, \(6 (3+2)\) does represent the area of the large rectangle. Remind students that “next to” implies multiplication.
By using the rectangle, we can tell that \(6 (3+2)=6 \boldcdot 3 + 6 \boldcdot 2\). This is another example of two expressions that are equivalent because of the distributive property.
Design Principle(s): Optimize output (for explanation)
9.3: Distributive Practice (15 minutes)
Activity
This is for practice going back and forth with the distributive property using numbers, but also to make the point that invoking the distributive property can help you do computations in your head. Some expressions that would be difficult to brute force become simpler after using the distributive property to write an equivalent expression.
Note that there is more than one way to rewrite the last row. For example, \(24-16\) could also be written as \(2(12-8)\) where \((12-8)\) is the difference of two terms. A term is a single number or variable, or variables and numbers multiplied together. This is fine, since there is no reason to insist that students use the greatest common factor at this time. Students should recognize that there is more than one factor that would work, and that the resulting expressions are equivalent. In a subsequent unit students will explicitly study the idea of a greatest common factor.
Launch
Give students the following setup: Suppose your business makes 15 items for $17 each and sells them for $20 each. How would you find your profit? One way is to write \(15\boldcdot 20 - 15\boldcdot 17\). But that’s a lot of calculations! An easier way to get the answer is to write \(15(20-17)\), which is easier to figure out in your head.
Allow students 10 minutes of quiet work time, followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
Complete the table. If you get stuck, skip an entry and come back to it, or consider drawing a diagram of two rectangles that share a side.
| column 1 | column 2 | column 3 | column 4 | value |
|---|---|---|---|---|
| \(5 \boldcdot 98\) | \(5 (100-2)\) | \(5 \boldcdot 100 - 5 \boldcdot 2\) | \(500 - 10\) | 490 |
| \(33 \boldcdot 12\) | \(33 (10 + 2)\) | |||
| \(3 \boldcdot 10 - 3 \boldcdot 4\) | \(30-12\) | |||
| \(100 (0.04 + 0.06)\) | ||||
| \(8 \boldcdot \frac 1 2 + 8 \boldcdot \frac 1 4\) | ||||
| \(9 + 12\) | ||||
| \(24 - 16\) |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- Use the distributive property to write two expressions that equal 360. (There are many correct ways to do this.)
- Is it possible to write an expression like \(a(b+c)\) that equals 360 where \(a\) is a fraction? Either write such an expression, or explain why it is impossible.
- Is it possible to write an expression like \(a(b-c)\) that equals 360? Either write such an expression, or explain why it is impossible.
- How many ways do you think there are to make 360 using the distributive property?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might understand how to expand an expression with parentheses but struggle with how to approach a sum. Encourage students to think about the rectangle diagrams they have seen and draw a diagram of a partitioned rectangle. Ask students what the sum represents and help them to see that it can represent the sum of the areas of the two smaller rectangles. Remind students that the rectangles have the same width, and ask what that width might have been to produce the two areas, what factor the two areas have in common. Then have them consider the other factors (the lengths) that would produce those products for the areas.
Activity Synthesis
Invite students to share their strategies and reasoning. Include students who used diagrams of partitioned rectangles. Ask if they noticed any interesting patterns, or if they want to share some examples of their own of calculations that can be made simpler by using the distributive property to write an equivalent expression.
Design Principle(s): Support sense-making; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Arrange students in groups of 2. One partner writes a product of the form \(a(b+c)\) or \(a(b-c)\). The other partner writes an equivalent expression using the distributive property, then each student evaluates their expression. The partners compare which computation was simpler, took less time, etc. Then have one partner write a sum and the other see if they can write an equivalent expression. Evaluate, compare, repeat as time allows. (It may be necessary to give students three numbers to use for the first round, instead of asking them to think of 3 numbers to use.)
9.4: Cool-down - Complete the Equation (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A term is a single number or variable, or variables and numbers multiplied together. Some examples of terms are 10, \(8x\), \(ab\), and \(7yz\).
When we need to do mental calculations, we often come up with ways to make the calculation easier to do mentally.
Suppose we are grocery shopping and need to know how much it will cost to buy 5 cans of beans at 79 cents a can. We may calculate mentally in this way:
\(5\boldcdot {79}\)
\(5\boldcdot {70}+5\boldcdot {9}\)
\(350+45\)
\(395\)
In general, when we multiply two terms (or factors), we can break up one of the factors into parts, multiply each part by the other factor, and then add the products. The result will be the same as the product of the two original factors. When we break up one of the factors and multiply the parts we are using the distributive property.
The distributive property also works with subtraction. Here is another way to find \(5\boldcdot 79\):
\(5\boldcdot 79\)
\(5\boldcdot {(80-1)}\)
\(400-5\)
\(395\)