Lesson 3
Staying in Balance
3.1: Hanging Around (10 minutes)
Warm-up
Students encounter and reason about a concrete situation, hangers with equal and unequal weights on each side. They then see diagrams of balanced and unbalanced hangers and think about what must be true and false about the situations. In subsequent activities, students will use the hanger diagrams to develop general strategies for solving equations.
Launch
Display the photo of socks and ask students, “What do you notice? What do you wonder?”

Give students 1 minute to think about the picture. Record their responses for all to see.
Things students may notice:
- There are two pink socks and two blue socks.
- The socks are clipped to either ends of two clothes hangers. The hangers are hanging from a rod.
- The hanger holding the pink socks is level; the hanger holding the blue socks is not level.
Things students may wonder:
- Why is the hanger holding the blue socks not level?
- Is something inside one of the blue socks to make it heavier than the other sock?
- What does this picture have to do with math?
Use the word “balanced” to describe the hanger on the left and “unbalanced” to describe the hanger on the right. Tell students that the hanger on the left is balanced because the two pink socks have an equal weight, and the hanger on the right is unbalanced because one blue sock is heavier than the other. Tell students that they will look at a diagram that is like the photo of socks, except with more abstract shapes, and they will reason about the weights of the shapes.
Give students 3 minutes of quiet work time followed by whole-class discussion.
Student Facing
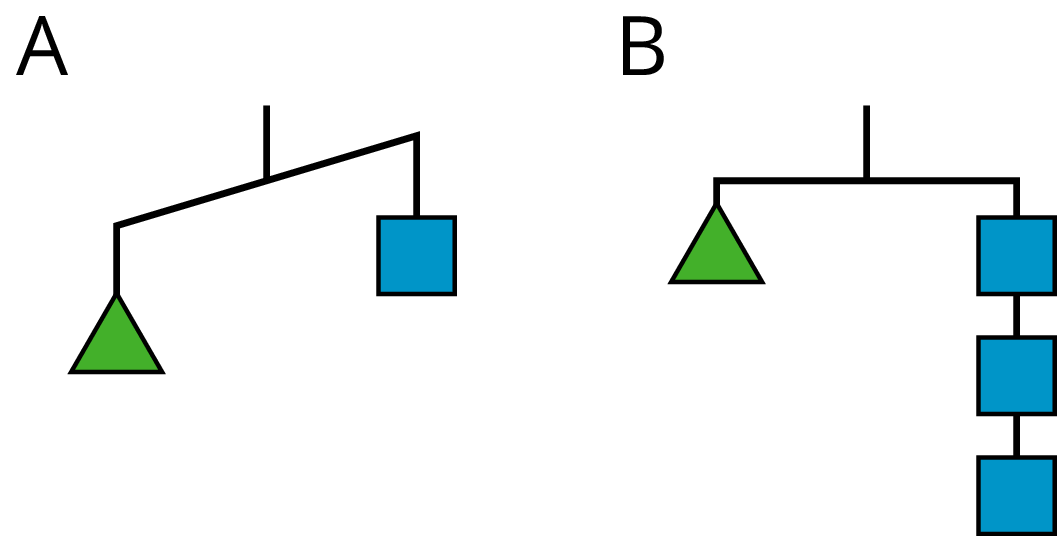
For diagram A, find:
- One thing that must be true
- One thing that could be true or false
- One thing that cannot possibly be true
For diagram B, find:
- One thing that must be true
- One thing that could be true or false
- One thing that cannot possibly be true
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share some things that must be true, could be true, and cannot possibly be true about the diagrams. Ask them to explain their reasoning. The purpose of this discussion is to understand how the hanger diagrams work. When the diagram is balanced, there is equal weight on each side. For example, since diagram B is balanced, we know that one triangle weighs the same as three squares. When the diagram is unbalanced, one side is heavier than the other. For example, since diagram A is unbalanced, we know that one triangle is heavier than one square.
3.2: Match Equations and Hangers (15 minutes)
Activity
Students are presented with four hanger diagrams and are asked to match an equation to each hanger. They analyze relationships and find correspondences between the two representations. Then students use the diagrams and equations to find the unknown value in each diagram. This value is a solution of the equation.
Notice that the hangers (and equations) for \(x\) and \(z\) are identical except that the variable appears on alternate sides of the equal sign. It may be obvious to some students that \(3z=6\) and \(6=3x\) mean the same thing mathematically, but we know that in grade 6 many students do not have a well-developed understanding of what the equal sign means. So it is worth spending a little time to make explicit that these equations each have the solution 2. When we are writing an equation, it means the same thing if the two sides are swapped. Generally, \(a=b\) means the same thing as \(b=a\) where \(a\) and \(b\) represent any mathematical expression.
Launch
Display the diagrams and explain that each square labeled with a 1 weighs 1 unit, and each shape labeled with a letter has an unknown weight.
Arrange students in groups of 2. Give 5–10 minutes of quiet work time and time to share their responses with a partner, followed by a whole-class discussion.
Design Principle(s): Support sense-making
Student Facing
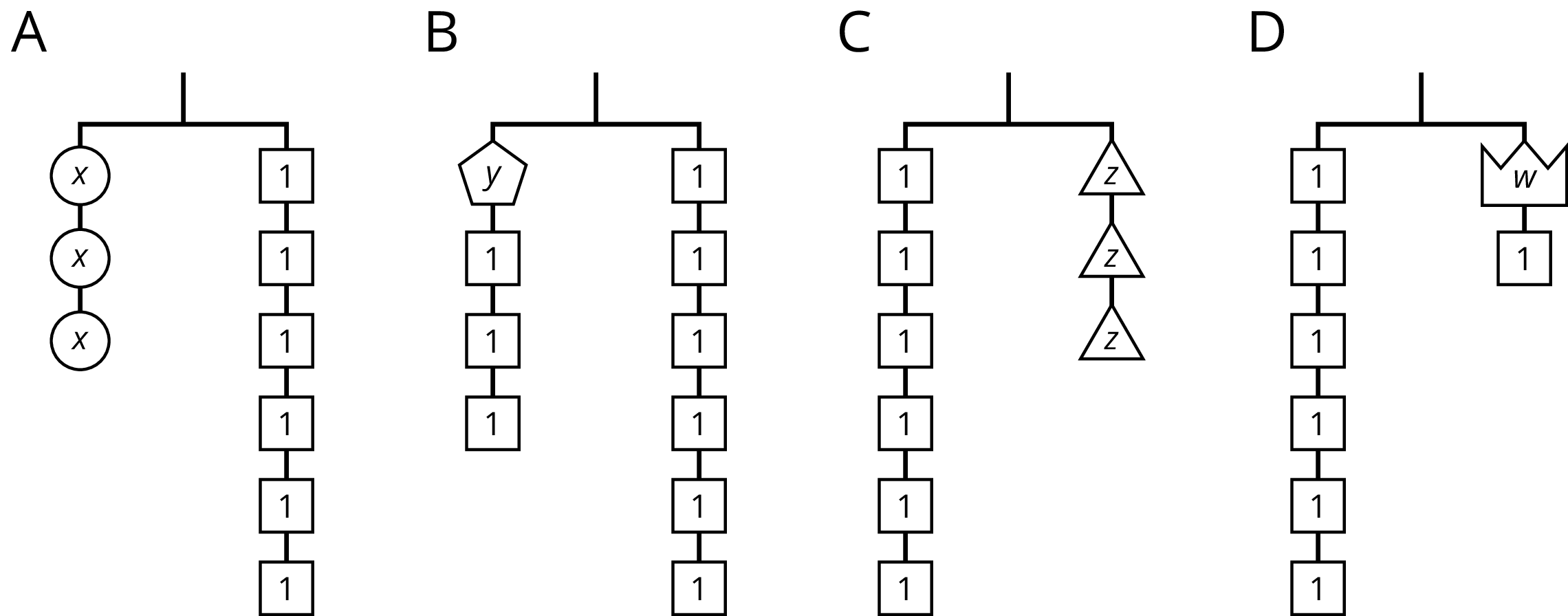
-
Match each hanger to an equation. Complete the equation by writing \(x\), \(y\), \(z\), or \(w\) in the empty box.
\(\boxed{\phantom{3}} + 3 = 6\)
\(3 \boldcdot \boxed{\phantom{3}} = 6\)
\(6 =\boxed{\phantom{3}} + 1\)
\(6 = 3 \boldcdot \boxed{\phantom{3}}\)
- Find a solution to each equation. Use the hangers to explain what each solution means.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Demonstrate two specific things for these specific examples: grouping the shapes on each side, and removing shapes from each side. In each case, the solution represents the weight of one shape. When you are done demonstrating, your diagrams might look like this:
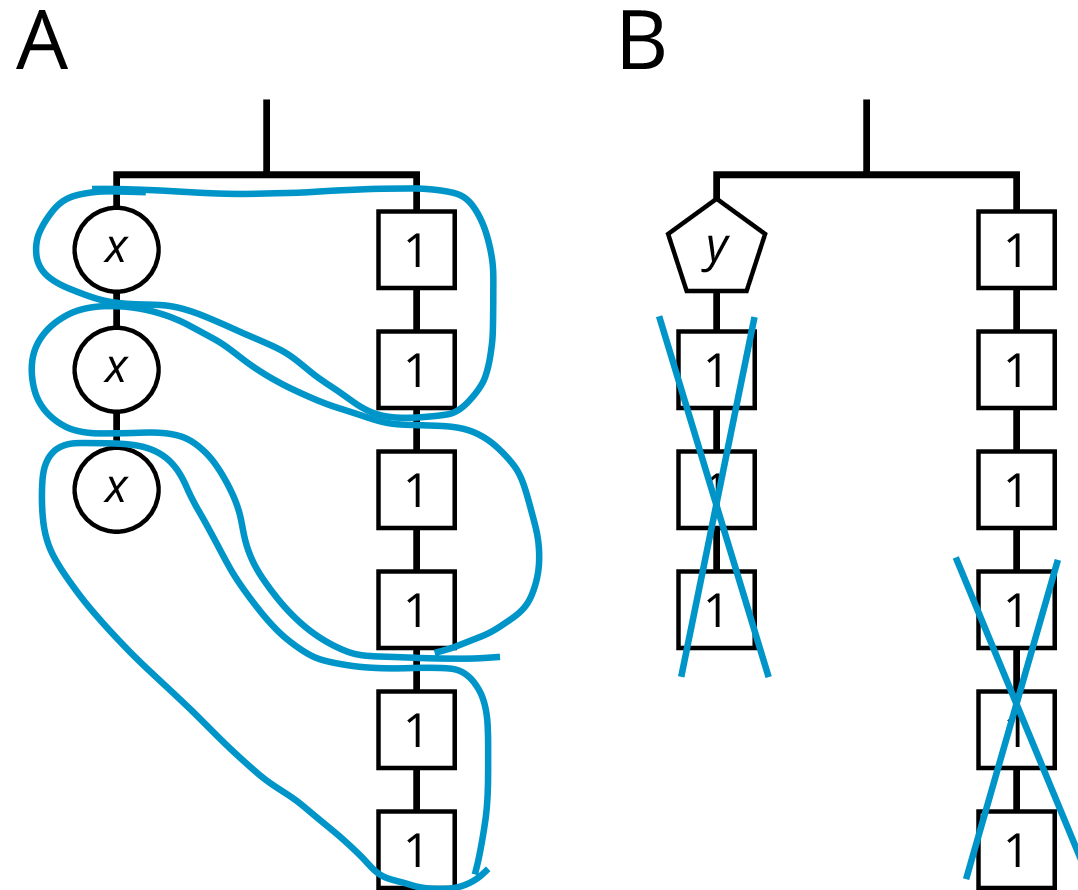
Consider asking some of the following questions:
- “Explain how you know from looking at a hanger that it can be represented by an equation involving addition.”
- “Explain how you know from looking at a hanger that it can be represented by an equation involving multiplication.”
- “What are some moves that ensure that a balanced hanger stays balanced?”
3.3: Connecting Diagrams to Equations and Solutions (15 minutes)
Activity
This activity continues the work of using a balanced hanger to develop strategies for solving equations. Students are presented with balanced hangers and are asked to write equations that represent them. They are then asked to explain how to use the diagrams, and then the equations, to reason about a solution. Students notice the structure of equations and diagrams and find correspondences between them and between solution strategies.
Launch
Draw students' attention to the diagrams in the task statement. Ensure they notice that the hangers are balanced and that each object is labeled with its weight. Some weights are labeled with numbers but some are unknown, so they are labeled with a variable.
Keep students in the same groups. Give 5–10 minutes of quiet work time and time to share their responses with a partner, followed by a whole-class discussion.
Supports accessibility for: Visual-spatial processing
Student Facing
Here are some balanced hangers. Each piece is labeled with its weight.
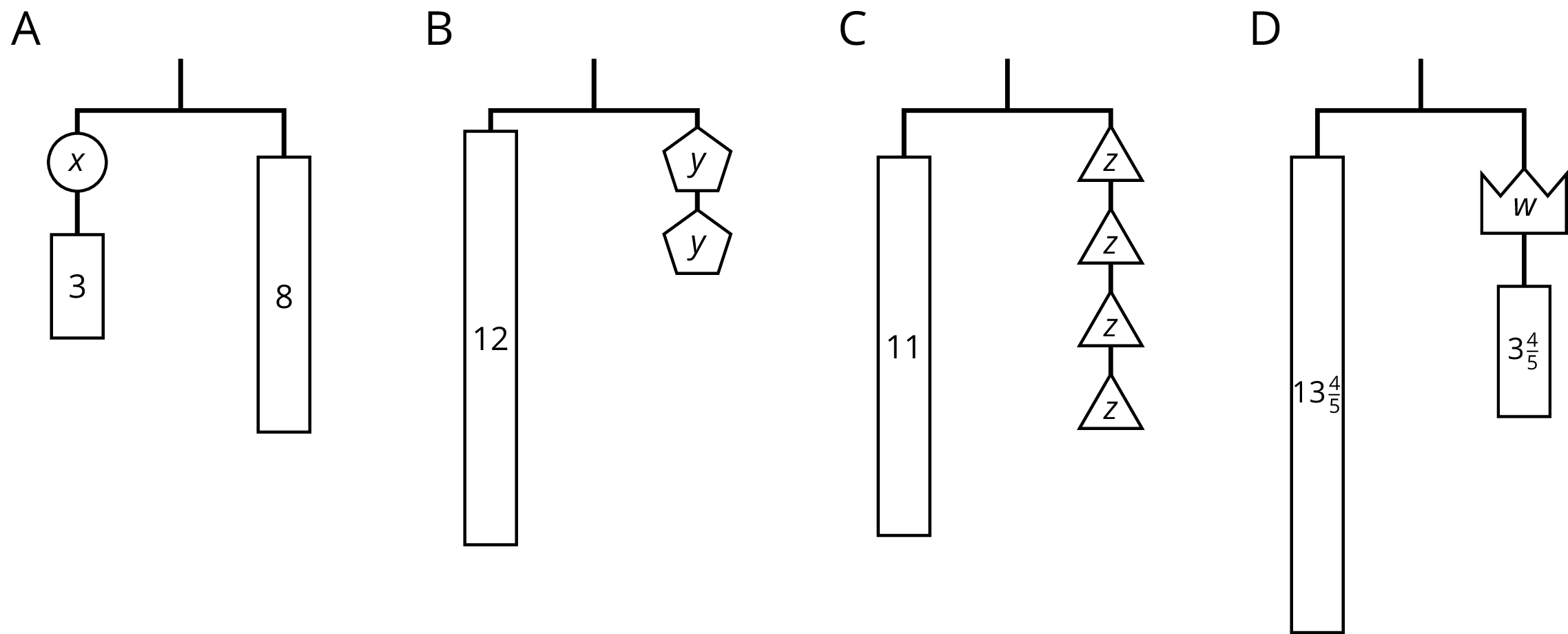
For each diagram:
- Write an equation.
-
Explain how to reason with the diagram to find the weight of a piece with a letter.
-
Explain how to reason with the equation to find the weight of a piece with a letter.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
When you have the time, visit the site https://solveme.edc.org/Mobiles.html to solve some trickier puzzles that use hanger diagrams like the ones in this lesson. You can even build new ones. (If you want to do this during class, check with your teacher first!)
Activity Synthesis
Invite students to demonstrate, side by side, how they reasoned with both the diagram and the equation. For example, diagram A can be shown next to the equation \(x+3=8\). Cross out a piece representing 3 from each side, and write \(x+3-3=8-3\), followed by \(x=5\). Repeat for all four diagrams. For the diagrams represented by a multiplication equation, show dividing each side into equal-sized groups.
We want students to walk away with two things:
- An instant recognition of the structure of equations of the form \(x+p=q\) and \(px=q\) where \(p\) and \(q\) are specific, given numbers.
- A visual representation in their mind that can be used to support understanding of why for equations of the form \(x+p=q\), you can subtract \(p\) from both sides, and for equations of the form \(px=q\), you can divide both sides by \(p\) to find the solution.
Design Principle(s): Optimize output; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Display the two equations \(5x=8\) and \(5+x=8\). Ask students to draw a hanger to match each equation. Then have them work with a partner to solve the equation alongside finding the unknown value on the hanger. Ask students to compare the two strategies and discuss how they are alike and how they are different.
3.4: Cool-down - Weight of the Circle (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A hanger stays balanced when the weights on both sides are equal. We can change the weights and the hanger will stay balanced as long as both sides are changed in the same way. For example, adding 2 pounds to each side of a balanced hanger will keep it balanced. Removing half of the weight from each side will also keep it balanced.
An equation can be compared to a balanced hanger. We can change the equation, but for a true equation to remain true, the same thing must be done to both sides of the equal sign. If we add or subtract the same number on each side, or multiply or divide each side by the same number, the new equation will still be true.
This way of thinking can help us find solutions to equations. Instead of checking different values, we can think about subtracting the same amount from each side or dividing each side by the same number.
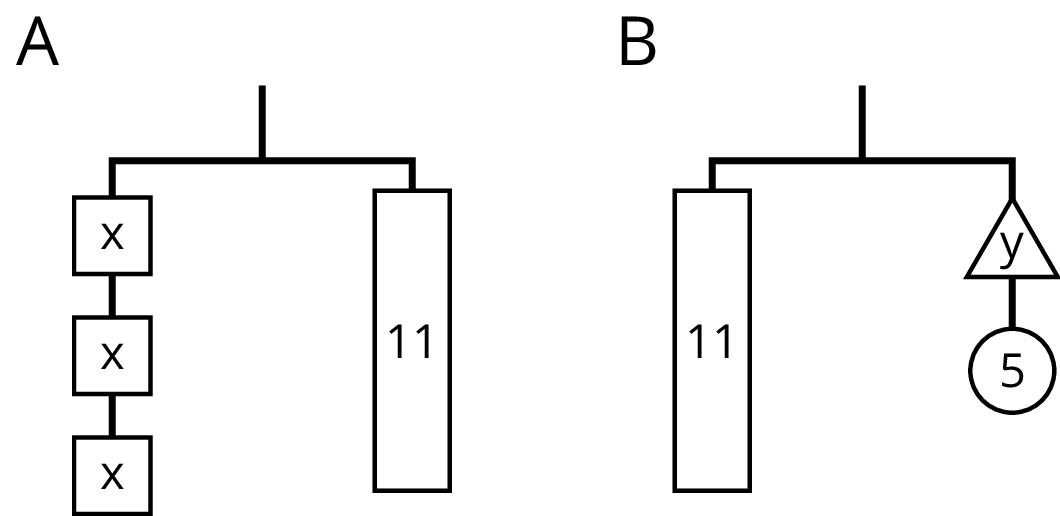
Diagram A can be represented by the equation \(3x=11\).
If we break the 11 into 3 equal parts, each part will have the same weight as a block with an \(x\).
Splitting each side of the hanger into 3 equal parts is the same as dividing each side of the equation by 3.
- \(3x\) divided by 3 is \(x\).
- 11 divided by 3 is \(\frac{11}{3}\).
- If \(3x=11\) is true, then \(x=\frac{11}{3}\) is true.
- The solution to \(3x=11\) is \(\frac{11}{3}\).
Diagram B can be represented with the equation \(11=y+5\).
If we remove a weight of 5 from each side of the hanger, it will stay in balance.
Removing 5 from each side of the hanger is the same as subtracting 5 from each side of the equation.
- \(11-5\) is 6.
- \(y+5-5\) is \(y\).
- If \(11=y+5\) is true, then \(6=y\) is true.
- The solution to \(11=y+5\) is 6.