Lesson 14

Evaluating Expressions with Exponents

View Student Lesson

14.1: Revisiting the Cube (10 minutes)

CCSS Standards


Addressing

Warm-up

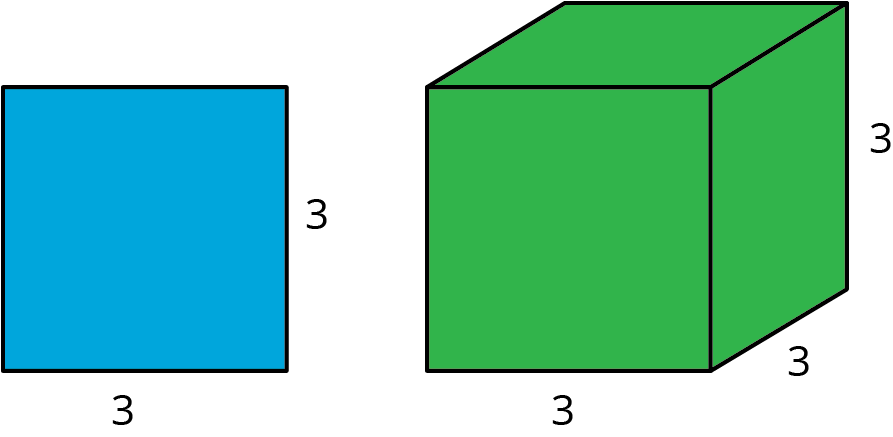
The purpose of this warm-up is for students to recall previous understandings of area, volume, and surface area of cubes, and how to record these measurements as expressions using exponents. Students might respond with either verbal or numerical descriptions, saying, for example, “We can find the area of the square,” or “The area of the square is 9 square units.”

After students share their responses, display the following table for all to see and give students time to discuss the information with a partner. The table is used to encourage students to think about the expressions with exponents in addition to the numeric responses.

  side length of the square area of the square volume of the cube surface area of the cube
as a number 3      
as an expression using an exponent 3      

Launch

Arrange students in groups of 2. Display the table and give students 1 minute of quiet work time to complete as much of the table as they can. Then complete the table and discuss as a group.

If students have access to digital activities they can explore the applet and generate dimensions that can be determined. After sharing, they can complete the table. 

Student Facing

Based on the given information, what other measurements of the square and cube could we find?

Student Response

For access, consult one of our IM Certified Partners.

Launch

Arrange students in groups of 2. Display the table and give students 1 minute of quiet work time to complete as much of the table as they can. Then complete the table and discuss as a group.

If students have access to digital activities they can explore the applet and generate dimensions that can be determined. After sharing, they can complete the table. 

Student Facing

Based on the given information, what other measurements of the square and cube could we find?

A square with a side length of three units. A cube with a side length of three units.

 

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

Ask students to share their responses for the cells in the table. Poll the students on whether they agree or disagree with each response. Record and display the responses for all to see. As students share responses, ask the following questions to help clarify their answers:

  • First row: What calculation did you do to arrive at that answer? Where are those measurements in the image?
  • Second row: How did you decide on the exponent for your answer? Where are those measurements in the image?
  side length of the square area of the square volume of the cube surface area of the cube
as a number 3 9 27 54
as an expression using an exponent 3 \(3^2\) \(3^3\) \(6(3^2)\)

In the next activity, students will analyze calculations of the surface area of a cube. Take time now to discuss why \(6(3^2)\) expresses the surface area of this cube. Ask students to think about how they computed surface area, and then analyze this expression. Where did the \(3^2\) come from? (It's the area of one face of the cube.) Why are we multiplying by 6? (We want to add up 6 \(3^2\)'s, and that is the same as multiplying \(3^2\) by 6.)

14.2: Calculating Surface Area (10 minutes)

CCSS Standards


Addressing

Routines and Materials


Instructional Routines

Activity

In this activity, students use surface area as a context to extend the order of operations to expressions with exponents. The context provides a reason to evaluate the exponent before performing the multiplication.

Launch

Give students 10 minutes of quiet work time, followed by a class discussion.

Reading: MLR6 Three Reads. Use this routine to support students’ comprehension of the situation. In the first read, students read the text with the goal of comprehending the situation (e.g., Jada and Noah have different solutions for the surface area of the same cube). In the second read, ask students to identify important quantities that can be counted or measured (e.g., the side length of the cube; the number of faces of a cube; the area of each face of the cube). In the third read, reveal the question, “Do you agree with either of them? Explain your reasoning.” Ask students to brainstorm possible strategies to answer the question (e.g., Find the area of each face of the cube. Multiply the area by 6 to find the surface area of the cube). This will help students concentrate on making sense of the situation before rushing to a solution or method.
Design Principle(s): Support sense-making

Student Facing

A cube has side length 10 inches. Jada says the surface area of the cube is 600 in2, and Noah says the surface area of the cube is 3,600 in2. Here is how each of them reasoned:

Jada’s Method:

\(6 \boldcdot 10^2\)
\(6 \boldcdot 100\)
\(600\)

Noah’s Method:

\(6 \boldcdot 10^2\)
\(60^2\)
\(3,\!600\)

Do you agree with either of them? Explain your reasoning.

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

In finding the surface area, there is a clear reason to find \(10^2\) and then multiply by 6. Tell students that sometimes it is not so clear in which order to evaluate operations. There is an order that we all generally agree on, and when we want something done in a different order, brackets are used to communicate what to do first. When an exponent occurs in the same expression as multiplication or division, we evaluate the exponent first, unless brackets say otherwise. Examples: \((3\boldcdot 4)^2 = 12^2 = 144\), since the brackets tell us to multiply \(3\boldcdot 4\) first. But \(3\boldcdot  4^2 = 3\boldcdot  16 = 48\), because since there are no brackets, we evaluate the exponent before multiplying.

If students bring up PEMDAS or another mnemonic for remembering the order of operations, point out that PEMDAS can be misleading in indicating multiplication before division, and addition before subtraction. Discuss the convention that brackets or parentheses indicate that something should be evaluated first, followed by exponents, multiplication, or division (evaluated left to right), and last, addition or subtraction (evaluated left to right).

14.3: Row Game: Expression Explosion (15 minutes)

CCSS Standards


Addressing

Routines and Materials


Instructional Routines

Activity

In this activity, students use the order of operations to evaluate expressions with exponents. They engage in MP3 as they listen and critique their partner’s reasoning when they do not agree on the answers.

Launch

Arrange students in groups of 2. Partners work individually on their expression in each row, then check their answers and discuss. Follow with a whole-class discussion.

Engagement: Develop Effort and Persistence. Encourage and support opportunities for peer interactions. Invite students to talk about their ideas with a partner before writing them down. Display sentence frames to support students when they work together to find errors. For example, “How did you . . .?”, “First, I _____ because…”, “I agree/disagree because . . .”
Supports accessibility for: Language; Social-emotional skills

Student Facing

Evaluate the expressions in one of the columns. Your partner will work on the other column. Check with your partner after you finish each row. Your answers in each row should be the same. If your answers aren’t the same, work together to find the error.

column A column B
\(5^2+4\) \(2^2+25\)
\(2^4 \boldcdot 5\) \(2^3 \boldcdot 10\)
\(3 \boldcdot 4^2\) \(12 \boldcdot 2^2\)
\(20+2^3\) \(1+3^3\)
\(9 \boldcdot 2^1\) \(3 \boldcdot 6^1\)
\(\frac19 \boldcdot \left( \frac12 \right)^3\) \(\frac18 \boldcdot \left( \frac13 \right)^2\)

 

Student Response

For access, consult one of our IM Certified Partners.

Student Facing

Are you ready for more?

  1. Consider this equation: \(\boxed{\phantom{3}}^2+\boxed{\phantom{3}}^2=\boxed{\phantom{3}}^2\). An example of 3 different whole numbers that could go in the boxes are 3, 4, and 5, since \(\displaystyle 3^2+4^2=5^2\). (That is, \(9+16=25\).)

    Can you find a different set of 3 whole numbers that make the equation true?

  2. How many sets of 3 different whole numbers can you find?
  3. Can you find a set of 3 different whole numbers that make this equation true? \(\boxed{\phantom{3}}^3+\boxed{\phantom{3}}^3=\boxed{\phantom{3}}^3\)
  4. How about this one? \(\boxed{\phantom{3}}^4+\boxed{\phantom{3}}^4=\boxed{\phantom{3}}^4\)

Once you have worked on this a little while, you can understand a problem that is famous in the history of math. (Alas, this space is too small to contain it.) If you are interested, consider doing some further research on Fermat’s Last Theorem.

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

The purpose of the discussion is to ensure that students understand and can apply the agreed on rules for order of operations when expressions contain exponents. Consider asking some of the following questions:

  • “Were there any expressions that were difficult to evaluate? Why were they difficult?”
  • “Did you disagree with your partner about any rows? How did you settle the disagreement?”
  • “Did you learn anything new about evaluating expressions with exponents?”
Reading, Writing, Speaking: MLR3 Clarify, Critique, Correct. Present an incorrect solution based on a common misconception about evaluating expressions with exponents. For example, “The expression \(1 + 3^3\) is equal to 64 because \(1 + 3\) is 4 and \(4^3\) is 64.” Ask students to identify the error, critique the reasoning, and revise the original statement. As students discuss in partners, listen for students who state that exponents must be evaluated before addition, unless parenthesis say otherwise. Therefore, \(3^3\) must be evaluated first before adding 1. This routine will engage students in meta-awareness as they critique and correct the language used to evaluate expressions with exponents.
Design Principles(s): Cultivate conversation; Maximize meta-awareness

Lesson Synthesis

Lesson Synthesis

Ask students to write and evaluate a numerical expression with an exponent and one other operation. Then have students switch with a partner and evaluate the partner's expressions. Invite some students to share their expressions with the class. 

14.4: Cool-down - Calculating Volumes (5 minutes)

CCSS Standards


Addressing

Cool-Down

For access, consult one of our IM Certified Partners.

Student Lesson Summary

Student Facing

Exponents give us a new way to describe operations with numbers, so we need to understand how exponents get along with the other operations we know.

When we write \(6 \boldcdot 4^2\), we want to make sure everyone agrees about how to evaluate this. Otherwise some people might multiply first and others compute the exponent first, and different people would get different values for the same expression!

Earlier we saw situations in which \(6 \boldcdot 4^2\) represented the surface area of a cube with side lengths 4 units. When computing the surface area, we evaluate \(4^2\) first (or find the area of one face of the cube first) and then multiply the result by 6. In many other expressions that use exponents, the part with an exponent is intended to be evaluated first.

To make everyone agree about the value of expressions like \(6 \boldcdot 4^2\), the convention is to evaluate the part of the expression with the exponent first. Here are a couple of examples:

\( \begin {align} 6 &\boldcdot 4^2 \\ 6 &\boldcdot 16 \\ &96 \end {align}\)

\( \begin {align} 45 &+ 5^2 \\ 45 &+ 25 \\ &70 \end {align}\)

If we want to communicate that 6 and 4 should be multiplied first and then squared, then we can use parentheses to group parts together:

\( \begin {align} (6 &\boldcdot 4)^2 \\ &24^2 \\ &576 \end {align}\)

\( \begin {align} (45 &+ 5)^2 \\ &50^2 \\ 2,&500 \end {align}\)