Lesson 10
The Distributive Property, Part 2
10.1: Possible Areas (5 minutes)
Warm-up
Students consider the area of a rectangle to reason about equivalent expressions and review symbolic notation for showing multiplication. This work supports the activities that follow, where students will explore and apply the distributive property by considering expressions for the areas of rectangles.
Launch
Allow students 2–3 minutes of quiet work time, followed by a whole-class discussion.
Student Facing
- A rectangle has a width of 4 units and a length of \(m\) units. Write an expression for the area of this rectangle.
-
What is the area of the rectangle if \(m\) is:
3 units?
2.2 units?
\(\frac15\) unit?
- Could the area of this rectangle be 11 square units? Why or why not?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students are struggling but they haven't drawn a diagram of a rectangle, suggest that they do so.
Activity Synthesis
Select students to share their response to each question. Points to highlight:
- Rectangle areas can be found by multiplying length by width.
- Both \(4m\) and \(m \boldcdot 4\) are expressions for the area of this rectangle. These are equivalent expressions.
- Lengths don’t have to be whole numbers. Neither do areas.
10.2: Partitioned Rectangles When Lengths are Unknown (10 minutes)
Activity
In this activity, students use expressions with variables to represent lengths of sides and areas of rectangles. These expressions are used to help students understand the distributive property and its use in creating equivalent expressions.
Launch
Arrange students in groups of 2–3. Allow students 5 minutes to work with their groups, followed by a quick whole-class discussion.
Supports accessibility for: Memory; Language
Design Principle(s): Support sense-making
Student Facing
-
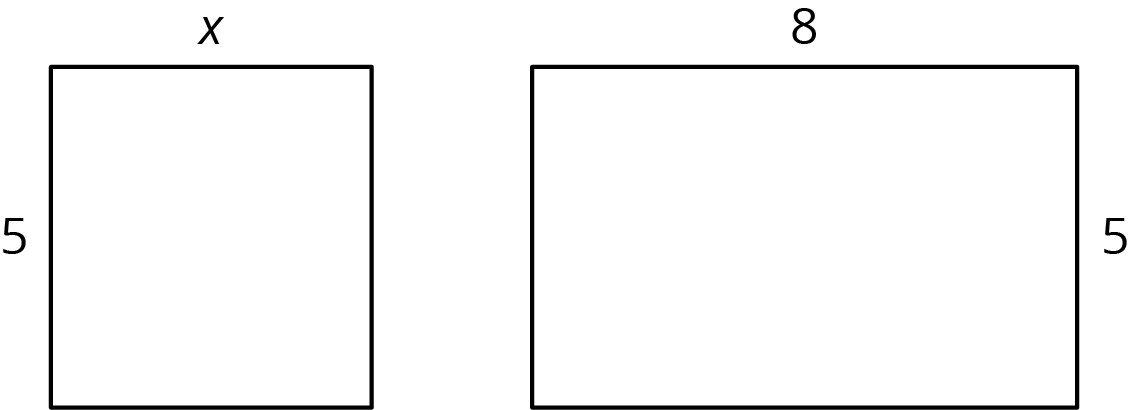
Here are two rectangles. The length and width of one rectangle are 8 and 5. The width of the other rectangle is 5, but its length is unknown so we labeled it \(x\).
Write an expression for the sum of the areas of the two rectangles.
-
The two rectangles can be composed into one larger rectangle as shown.
What are the width and length of the new, large rectangle?
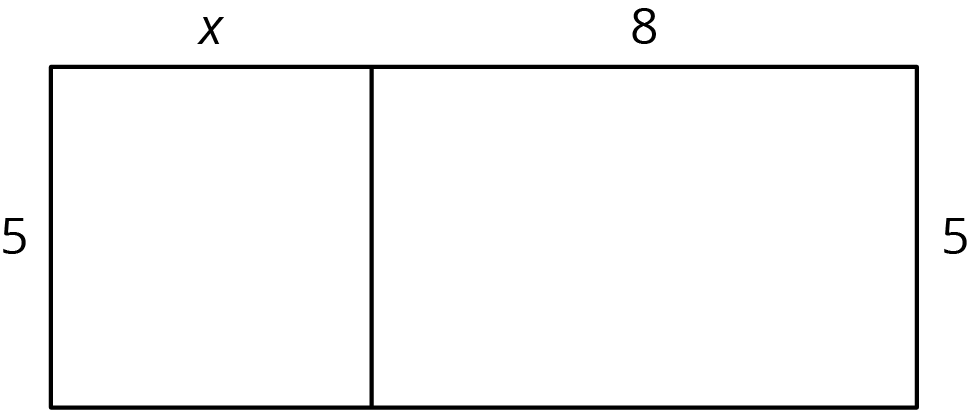
- Write an expression for the total area of the large rectangle as the product of its width and its length.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Solicit students’ responses to the first and third questions. Display two expressions for all to see. Expressions that are equivalent to these are fine; ensure everyone agrees that one is an acceptable response to the first question and the other is an acceptable response to the third question.
\(\displaystyle 5 \boldcdot x + 5 \boldcdot 8\)
\(\displaystyle 5(x+8)\)
Ask students to look at the two expressions and think of something they notice and wonder. Here are some things that students might notice.
- The 5 appears twice in one expression and only once in the other.
- These expressions must be equivalent to each other, because they each represent the area of the same region.
- These look like an example of the distributive property, but with a letter.
10.3: Areas of Partitioned Rectangles (20 minutes)
Activity
In this activity students are presented with several partitioned rectangles. They identify the length and width for each rectangle, and then write expressions for the area in two different ways: first as the product of the length times the width, where one of these measurements will be expressed as a sum, and then as the sum of the areas of the smaller rectangles that make up the large rectangle. Students reason that these two expressions must be equal since they both represent the total area of the partitioned rectangle. In this way they see several examples of the distributive property. Students may choose to assign values to the variable in each rectangle to check that their expressions for area are equal.
Launch
Keep students in the same groups. Allow students 10 minutes to work with their groups, followed by a whole-class discussion.
Supports accessibility for: Memory; Conceptual processing
Design Principle(s): Maximize meta-awareness
Student Facing
For each rectangle, write expressions for the length and width and two expressions for the total area. Record them in the table. Check your expressions in each row with your group and discuss any disagreements.
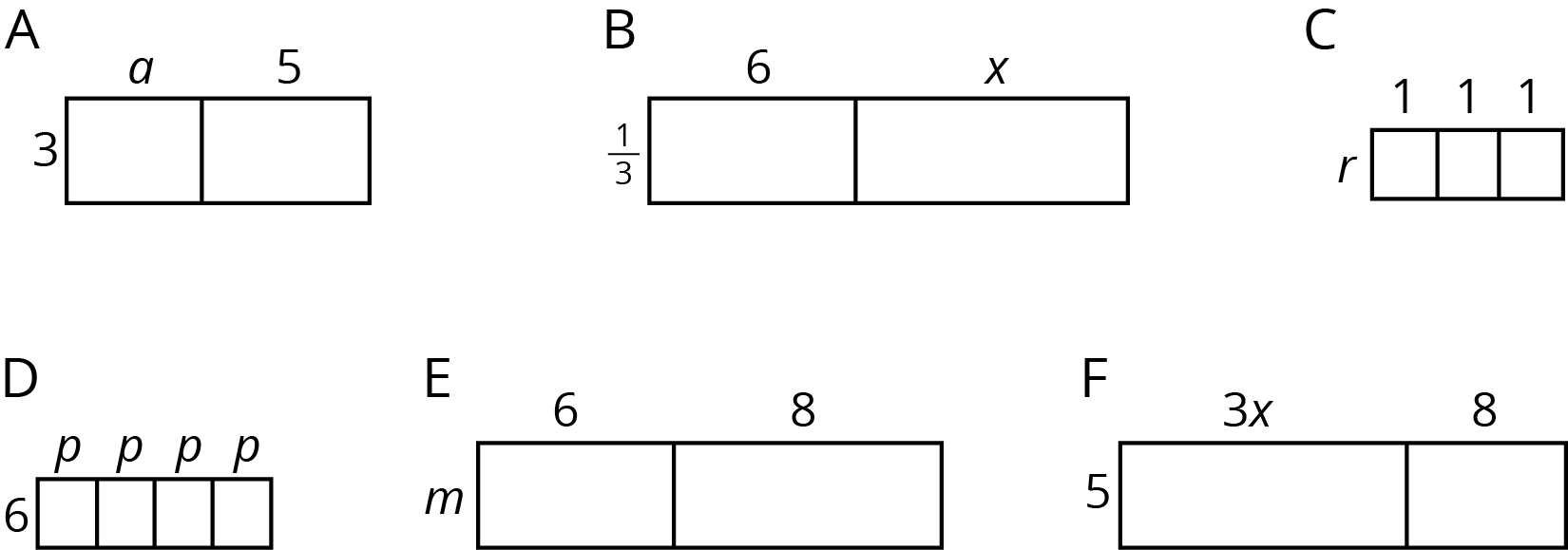
| rectangle | width | length | area as a product of width times length |
area as a sum of the areas of the smaller rectangles |
|---|---|---|---|---|
|
A |
||||
|
B |
||||
|
C |
||||
|
D |
||||
|
E |
||||
|
F |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Here is an area diagram of a rectangle.

- Find the lengths \(w\), \(x\), \(y\), and \(z\), and the area \(A\). All values are whole numbers.
- Can you find another set of lengths that will work? How many possibilities are there?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is to help students understand the distributive property and how it can be used to generate equivalent expressions.
Remind students about the term “coefficient” and the convention of writing the coefficient before the variable. Ask students why we consider one expression for area “a sum” and the other “a product” even though both expressions contain sums and products. (For example, we take \(6x + 8\) to be a sum because we are adding two terms \(6x\) and 8, even though \(6x\) is actually a product of 6 and \(x\). Likewise, we take \(2(3x +4)\) to be a product because we note that 2 is multiplied by the quantity \(3x + 4\), which contains a sum and a product.)
When appropriate, encourage students to use the word term to refer to things like \(3a\), \(6p\), and \(15x\).
Finally, we want to make the point another way that each pair of expressions they wrote are equivalent to each other. For example, we can see that \(5(3x+8)\) and \(15x+40\) are equivalent because they both represent the area of figure G. However, we want to reinforce what equivalent means here. Ask each pair of students to choose any number, and evaluate both \(5(3x+8)\) and \(15x+40\) using the value they chose for \(x\). No matter what value they choose, the expressions will yield the same value. For example, if they choose 2 as the value for \(x\), \(5(3 \boldcdot 2 + 8)\) is 70, and \(15 \boldcdot 2 + 40\) is also 70.
Lesson Synthesis
Lesson Synthesis
Ask students to compare the expressions they saw today with the expressions they saw in the last lesson. How are they alike? How are they different? Students should see that their work with expressions containing variables is an extension of the work they did in the last lesson with numbers.
Invite students to share any disagreements that arose within their group and how they were resolved.
10.4: Cool-down - Which Expressions Represent Area? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here is a rectangle composed of two smaller rectangles A and B.
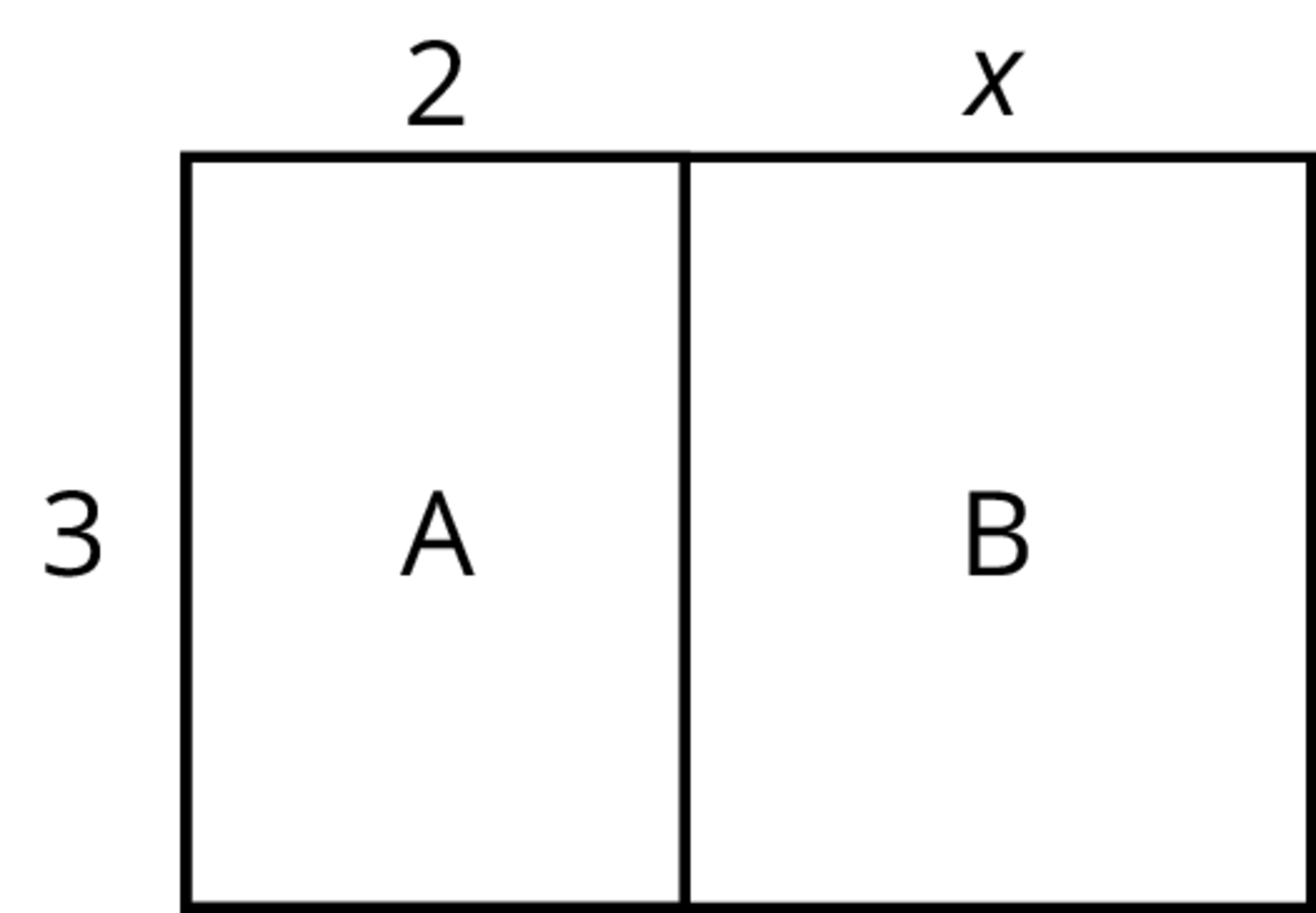
Based on the drawing, we can make several observations about the area of the rectangle:
- One side length of the large rectangle is 3 and the other is \(2+x\), so its area is \(3(2+x)\).
- Since the large rectangle can be decomposed into two smaller rectangles, A and B, with no overlap, the area of the large rectangle is also the sum of the areas of rectangles A and B: \(3(2) + 3(x)\) or \(6+3x\).
- Since both expressions represent the area of the large rectangle, they are equivalent to each other. \(3(2+x)\) is equivalent to \(6 + 3x\).
We can see that multiplying 3 by the sum \(2+x\) is equivalent to multiplying 3 by 2 and then 3 by \(x\) and adding the two products. This relationship is an example of the distributive property.
\(\displaystyle 3(2+x) = 3 \boldcdot 2 + 3 \boldcdot x\)