Lesson 5

The Size of the Scale Factor

View Student Lesson

Problem 1

Rectangles P, Q, R, and S are scaled copies of one another. For each pair, decide if the scale factor from one to the other is greater than 1, equal to 1, or less than 1.

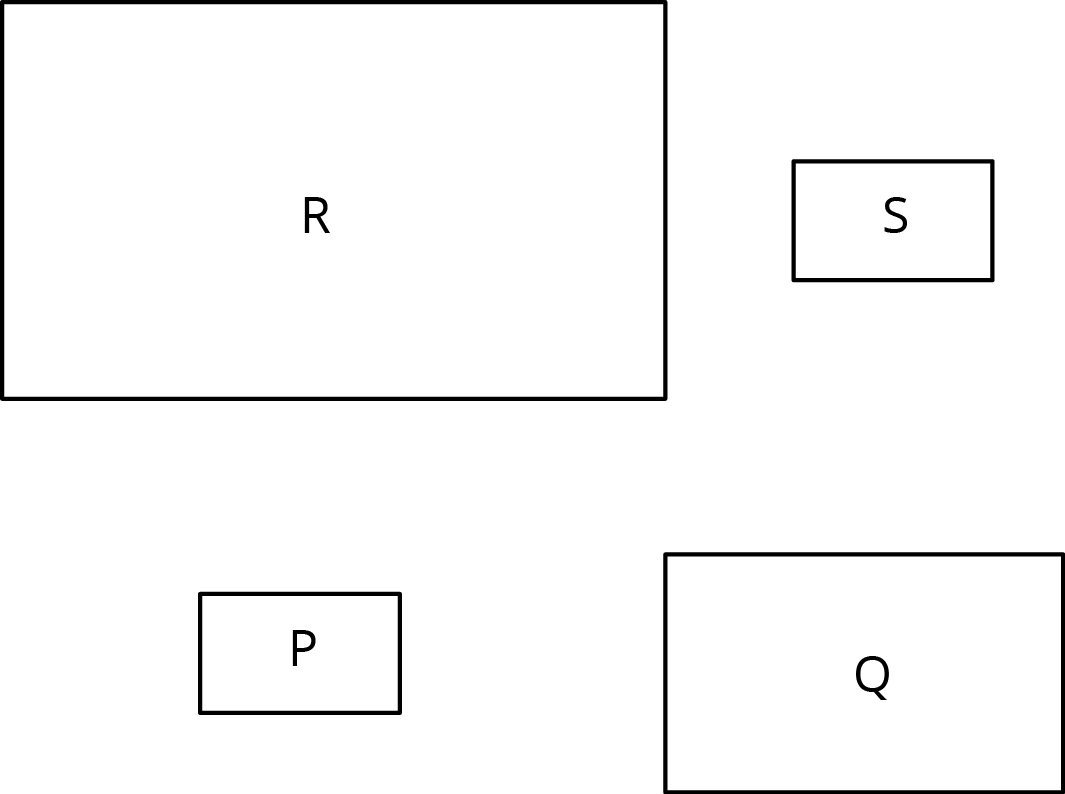
Four rectangles, labeled P, Q, R and S. 
  1. from P to Q
  2. from P to R
  3. from Q to S
  4. from Q to R
  5. from S to P
  6. from R to P
  7. from P to S

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Triangle S and Triangle L are scaled copies of one another.

  1. What is the scale factor from S to L?

  2. What is the scale factor from L to S?

  3. Triangle M is also a scaled copy of S. The scale factor from S to M is \(\frac{3}{2}\). What is the scale factor from M to S?

Two triangles labeled S and L on a grid. Triangle S has a horizontal base of 2 units and a height of 4 units. Triangle L has a horizontal base of 4 units and a height of 8 units.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Are two squares with the same side lengths scaled copies of one another? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Quadrilateral A has side lengths 2, 3, 5, and 6. Quadrilateral B has side lengths 4, 5, 8, and 10. Could one of the quadrilaterals be a scaled copy of the other? Explain.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 2.)

Problem 5

Select all the ratios that are equivalent to the ratio \(12:3\).

A:

\(6:1\)

B:

\(1:4\)

C:

\(4:1\)

D:

\(24:6\)

E:

\(15:6\)

F:

\(1,\!200:300\)

G:

\(112:13\)

Solution

For access, consult one of our IM Certified Partners.