Lesson 4

Scaled Relationships

Let’s find relationships between scaled copies.

4.1: Three Quadrilaterals (Part 1)

Each of these polygons is a scaled copy of the others.

Polygon A, B, C, D. Polygon E, F, G, H. Polygon I, J, K, L.
  1. Name two pairs of corresponding angles. What can you say about the sizes of these angles?
  2. Check your prediction by measuring at least one pair of corresponding angles using a protractor. Record your measurements to the nearest \(5^\circ\).

4.2: Three Quadrilaterals (Part 2)

Each of these polygons is a scaled copy of the others. You already checked their corresponding angles.

Polygon A, B, C, D. Polygon E, F, G, H. Polygon I, J, K, L.
  1. The side lengths of the polygons are hard to tell from the grid, but there are other corresponding distances that are easier to compare. Identify the distances in the other two polygons that correspond to \(DB\) and \(AC\), and record them in the table.
    quadrilateral distance that
    corresponds to \(DB\)     		distance that
    corresponds to \(AC\)
    \(ABCD\) \(DB = 4\) \(AC = 6\)
    \(EFGH\)
    \(IJKL\)

  2. Look at the values in the table. What do you notice?

    Pause here so your teacher can review your work.

  3. The larger figure is a scaled copy of the smaller figure.

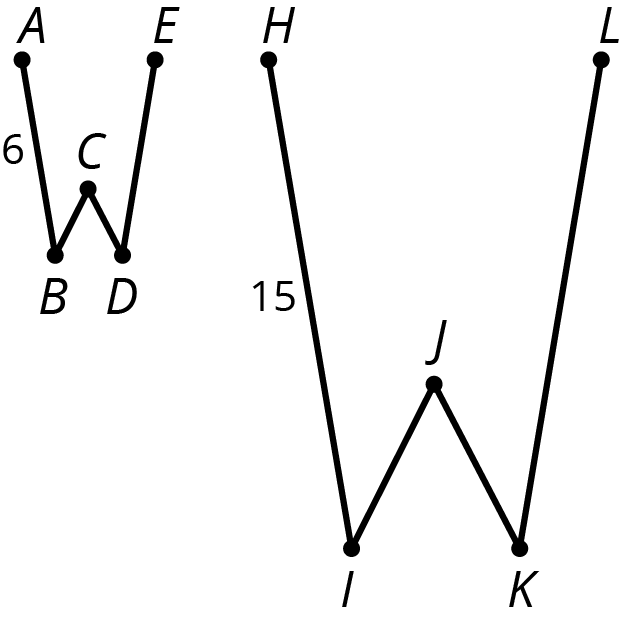
    Two figures of the letter W.
    1. If \(AE = 4\), how long is the corresponding distance in the second figure? Explain or show your reasoning.
    2. If \(IK = 5\), how long is the corresponding distance in the first figure? Explain or show your reasoning.

4.3: Scaled or Not Scaled?

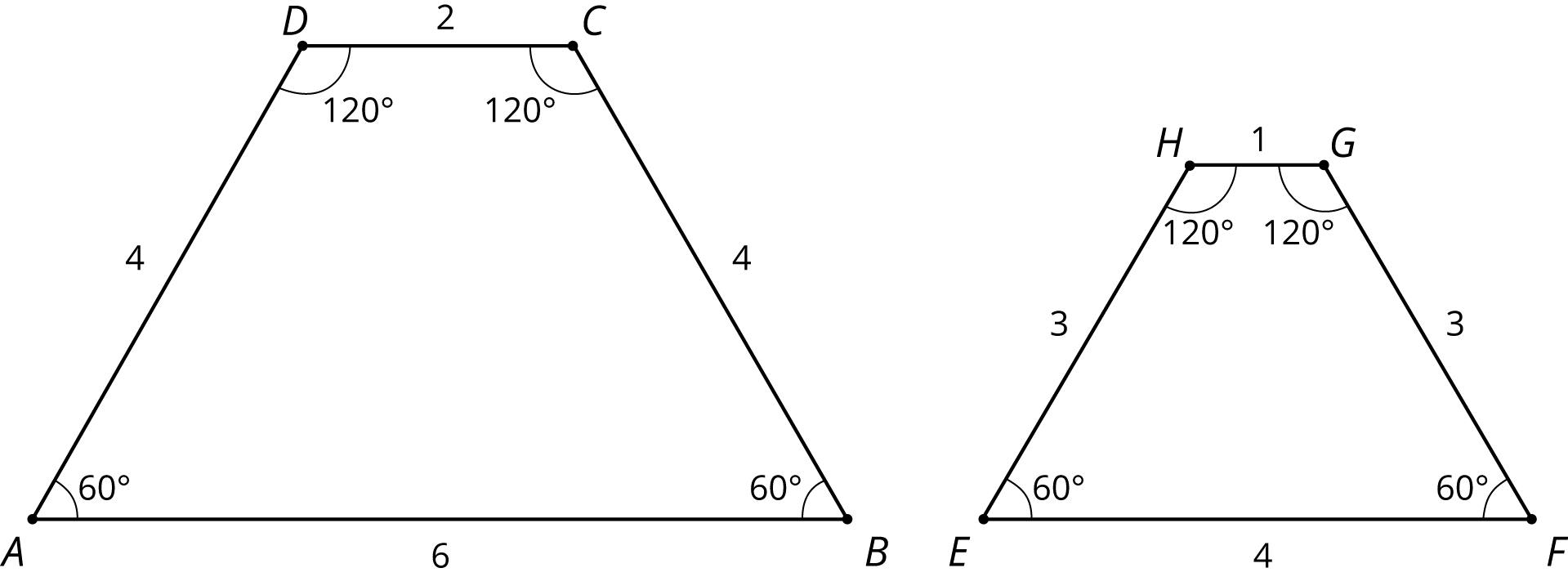
Here are two quadrilaterals.

Two quadrilaterals on a coordinate plane
  1. Mai says that Polygon \(ZSCH\) is a scaled copy of Polygon \(XJYN\), but Noah disagrees. Do you agree with either of them? Explain or show your reasoning.
  2. Record the corresponding distances in the table. What do you notice?
    quadrilateral horizontal distance vertical distance
    \(XJYN\) \(XY = \phantom{33}\) \(JN = \phantom{33}\)
    \(ZSCH\) \(ZC = \phantom{33}\) \(SH = \phantom{33}\)
  3. Measure at least three pairs of corresponding angles in \(XJYN\) and \(ZSCH\) using a protractor. Record your measurements to the nearest \(5^\circ\). What do you notice?
  4. Do these results change your answer to the first question? Explain.

  5. Here are two more quadrilaterals.

    2 trapezoids with side lengths and angle measurements provided 
    Kiran says that Polygon \(EFGH\) is a scaled copy of \(ABCD\), but Lin disagrees. Do you agree with either of them? Explain or show your reasoning.


All side lengths of quadrilateral \(MNOP\) are 2, and all side lengths of quadrilateral \(QRST\) are 3. Does \(MNOP\) have to be a scaled copy of \(QRST\)? Explain your reasoning.

4.4: Comparing Pictures of Birds

Here are two pictures of a bird. Find evidence that one picture is not a scaled copy of the other. Be prepared to explain your reasoning.

Summary

When a figure is a scaled copy of another figure, we know that:

  • All distances in the copy can be found by multiplying the corresponding distances in the original figure by the same scale factor, whether or not the endpoints are connected by a segment.

    For example, Polygon \(STUVWX\) is a scaled copy of Polygon \(ABCDEF\). The scale factor is 3. The distance from \(T\) to \(X\) is 6, which is three times the distance from \(B\) to \(F\).

Polygon ABCDEF and its scaled copy Polygon STUVWX.
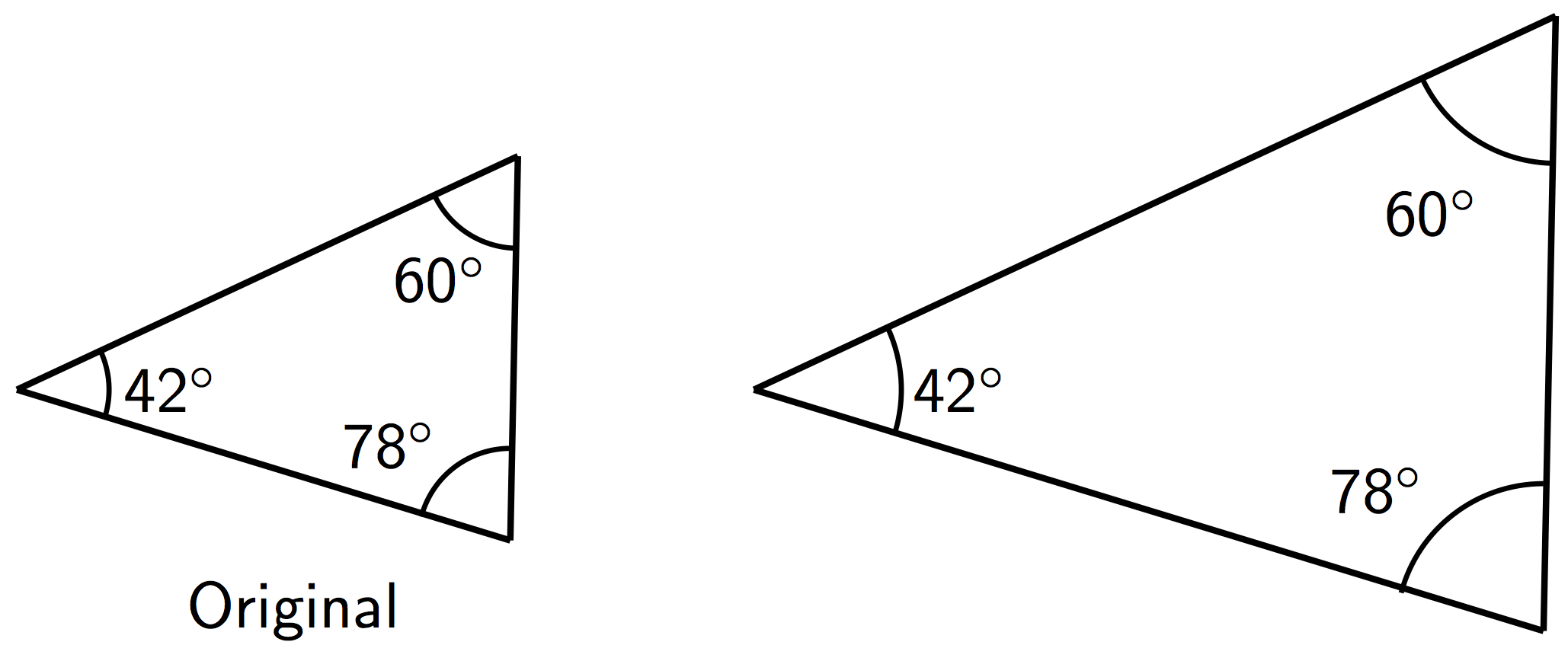
  • All angles in the copy have the same measure as the corresponding angles in the original figure, as in these triangles.
Original triangle has angle measures 42, 60, and 78 degrees. The larger, scaled version of the triangle has angle measures 42, 60, and 78 degrees.

These observations can help explain why one figure is not a scaled copy of another.

For example, even though their corresponding angles have the same measure, the second rectangle is not a scaled copy of the first rectangle, because different pairs of corresponding lengths have different scale factors, \(2 \boldcdot \frac12 = 1\) but \(3 \boldcdot \frac23 = 2\).

The first rectangle has height 2 and length 3. The second rectangle has height 1 and length 2.

Video Summary

Video VLS G7U1V1 Scaled Copies (Lessons 1–4) available at https://player.vimeo.com/video/442940614.

Glossary Entries

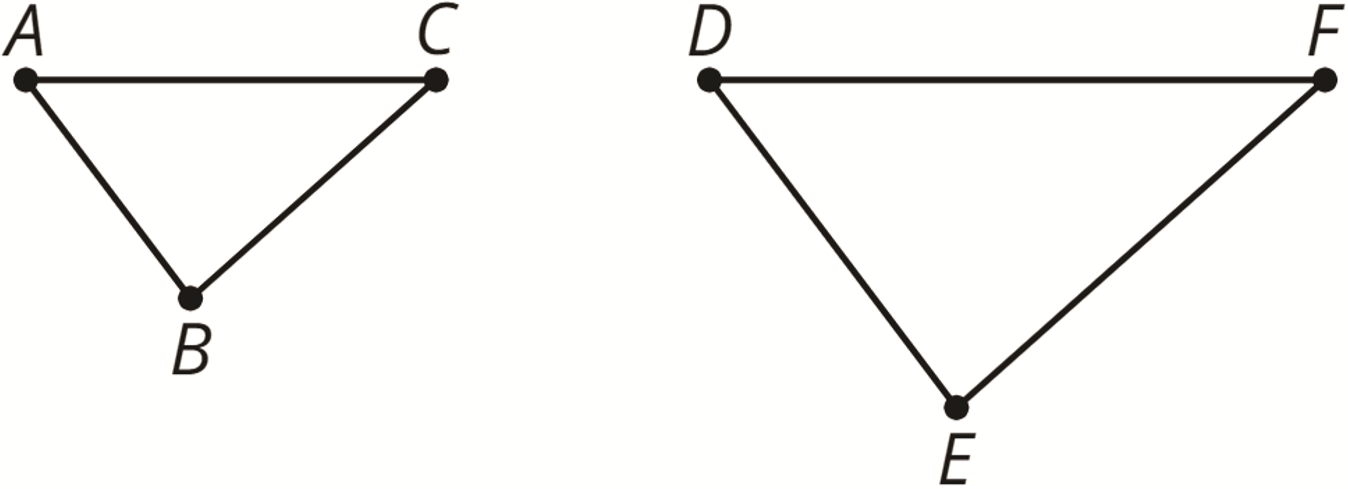
  • corresponding

    When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

    For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).

    2 triangles with corresponding parts
  • scale factor

    To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

    In this example, the scale factor is 1.5, because \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).

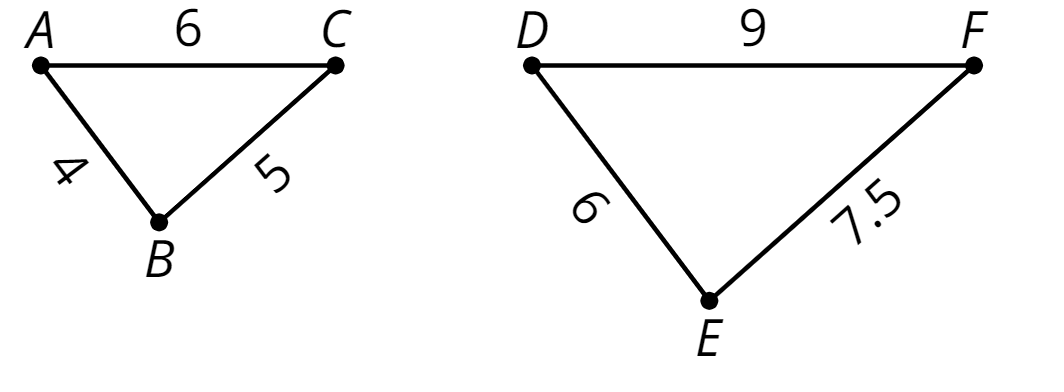
    2 triangles
  • scaled copy

    A scaled copy is a copy of a figure where every length in the original figure is multiplied by the same number.

    For example, triangle \(DEF\) is a scaled copy of triangle \(ABC\). Each side length on triangle \(ABC\) was multiplied by 1.5 to get the corresponding side length on triangle \(DEF\).

    2 triangles