Lesson 3

Making Scaled Copies

Let’s draw scaled copies.

3.1: More or Less?

For each problem, select the answer from the two choices.

  1. The value of \(25\boldcdot (8.5)\) is:

    1. More than 205
    2. Less than 205

  2. The value of \((9.93)\boldcdot (0.984)\) is:

    1. More than 10
    2. Less than 10

  3. The value of \((0.24)\boldcdot (0.67)\) is:

    1. More than 0.2
    2. Less than 0.2

3.2: Drawing Scaled Copies

Five drawings on a grid, labeled A, B,C,D,E.
  1. Draw a scaled copy of either Figure A or B using a scale factor of 3.
  2. Draw a scaled copy of either Figure C or D using a scale factor of \(\frac12\).

3.3: Which Operations? (Part 1)

Diego and Jada want to scale this polygon so the side that corresponds to 15 units in the original is 5 units in the scaled copy.

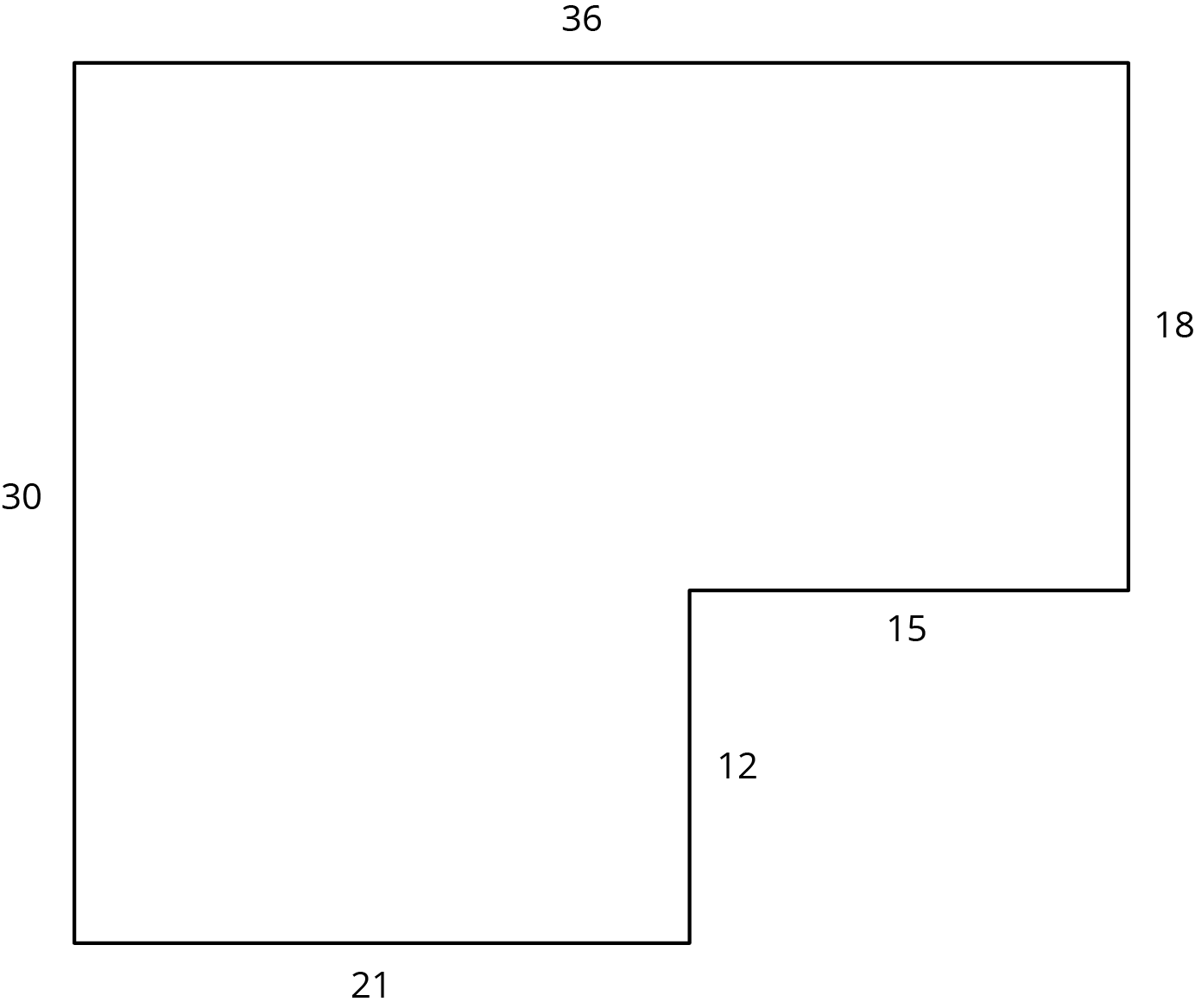
Original polygon is a rectangle of height 30 and length 36 with a rectangle of height 12 and length 15 removed from the bottom right corner.

Diego and Jada each use a different operation to find the new side lengths. Here are their finished drawings.

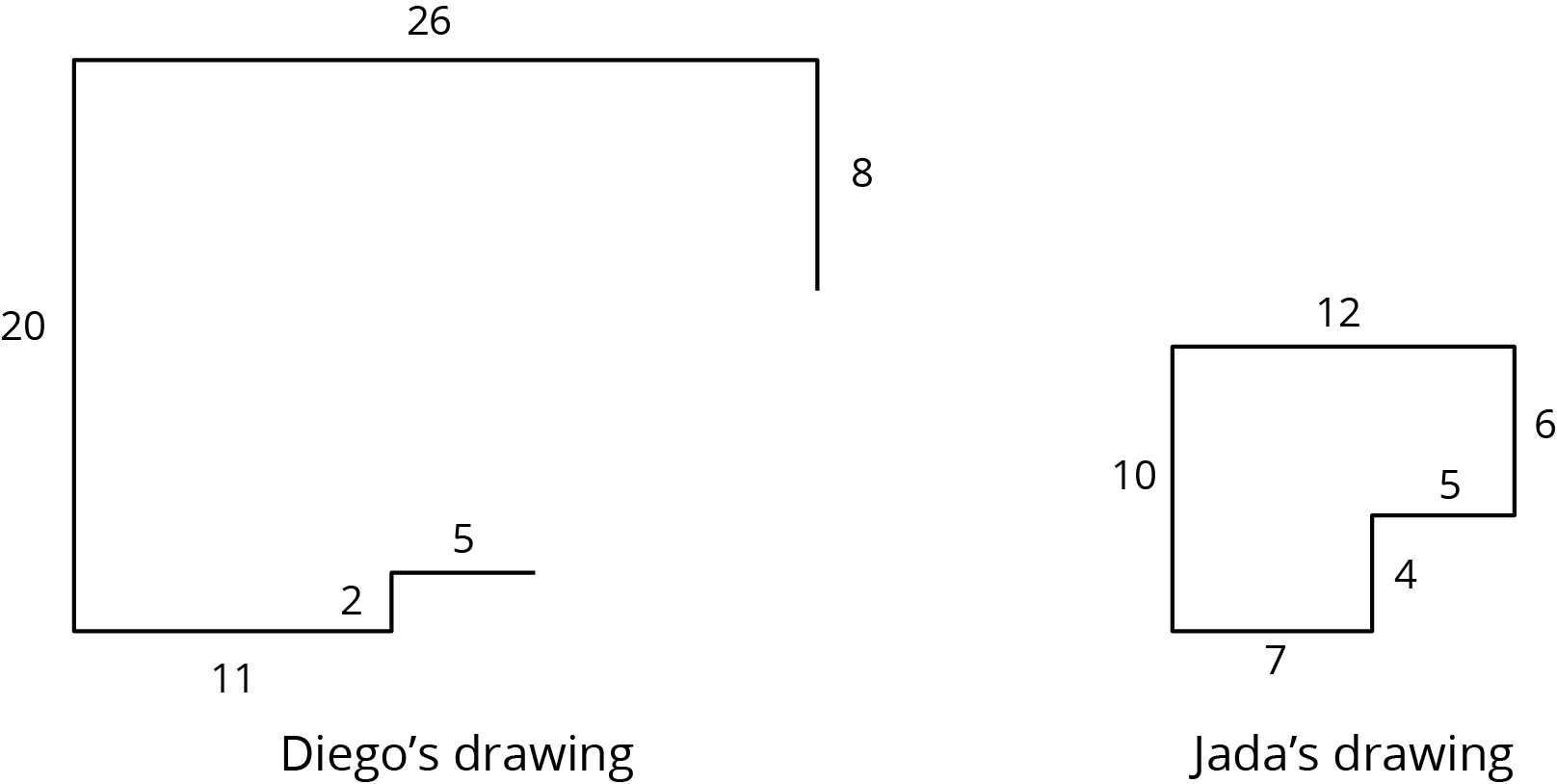
Diego’s and Jada’s drawings of irregular shapes.
  1. What operation do you think Diego used to calculate the lengths for his drawing?
  2. What operation do you think Jada used to calculate the lengths for her drawing?
  3. Did each method produce a scaled copy of the polygon? Explain your reasoning.

3.4: Which Operations? (Part 2)

Andre wants to make a scaled copy of Jada's drawing so the side that corresponds to 4 units in Jada’s polygon is 8 units in his scaled copy.

  1. Andre says “I wonder if I should add 4 units to the lengths of all of the segments?” What would you say in response to Andre? Explain or show your reasoning.

  2. Create the scaled copy that Andre wants. If you get stuck, consider using the edge of an index card or paper to measure the lengths needed to draw the copy.

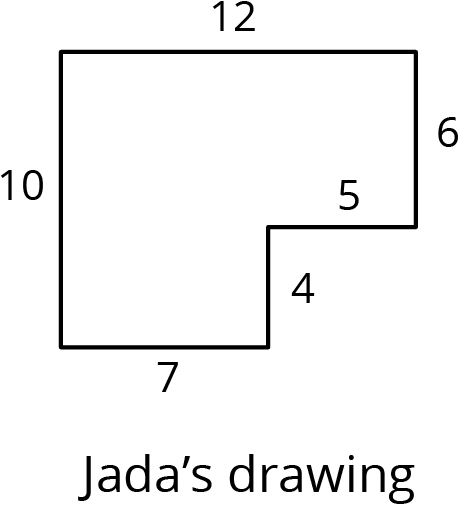
    A polygon with side lengths 12, 6, 5, 4, 7, and 10.


The side lengths of Triangle B are all 5 more than the side lengths of Triangle A. Can Triangle B be a scaled copy of Triangle A? Explain your reasoning.

Summary

Creating a scaled copy involves multiplying the lengths in the original figure by a scale factor.

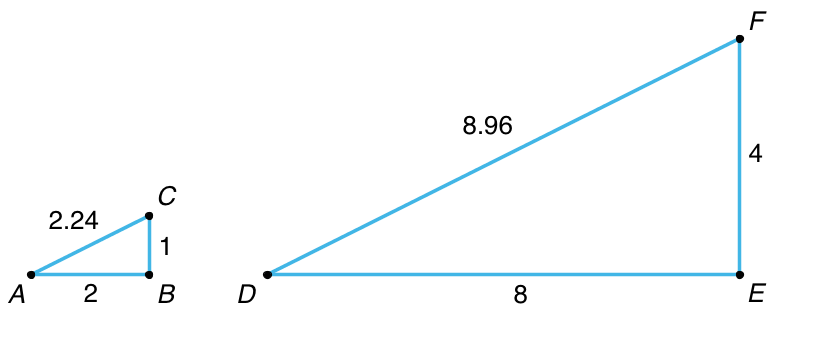
For example, to make a scaled copy of triangle \(ABC\) where the base is 8 units, we would use a scale factor of 4. This means multiplying all the side lengths by 4, so in triangle \(DEF\), each side is 4 times as long as the corresponding side in triangle \(ABC\).

Triangle A, B, C has side lengths 2, 1, and 2.24. Triangle D, E, F has side lengths 8, 4, and 8.96.

Glossary Entries

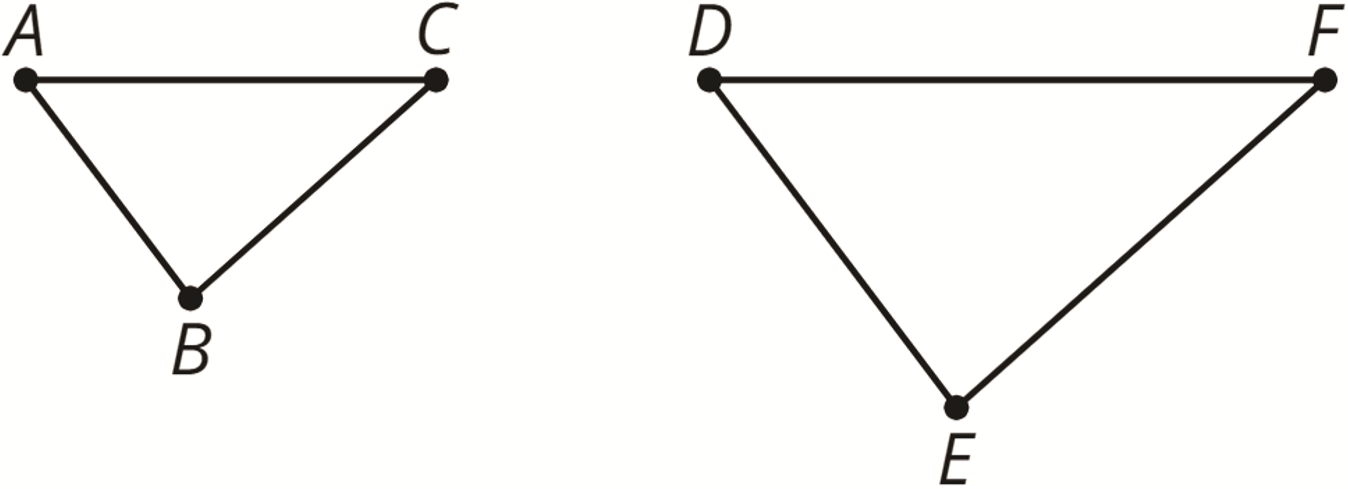
  • corresponding

    When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

    For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).

    2 triangles with corresponding parts
  • scale factor

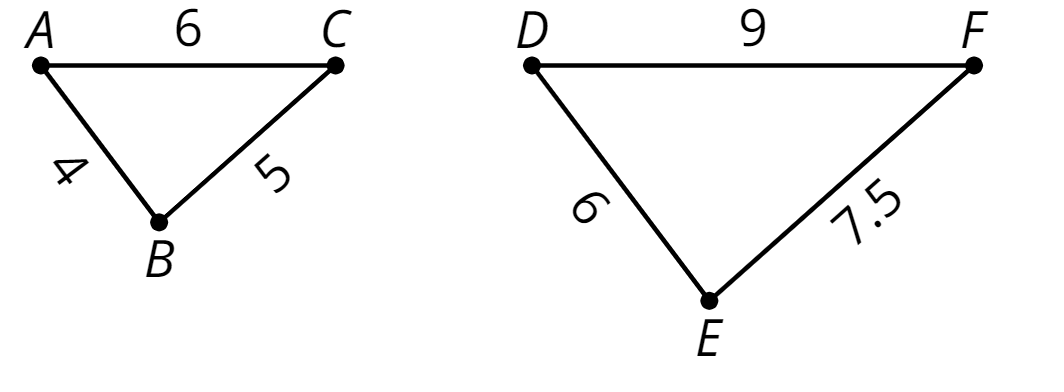
    To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

    In this example, the scale factor is 1.5, because \(4 \boldcdot (1.5) = 6\), \(5 \boldcdot (1.5)=7.5\), and \(6 \boldcdot (1.5)=9\).

    2 triangles
  • scaled copy

    A scaled copy is a copy of a figure where every length in the original figure is multiplied by the same number.

    For example, triangle \(DEF\) is a scaled copy of triangle \(ABC\). Each side length on triangle \(ABC\) was multiplied by 1.5 to get the corresponding side length on triangle \(DEF\).

    2 triangles