Lesson 3

Staying in Balance

View Student Lesson

Problem 1

Select all the equations that represent the hanger.

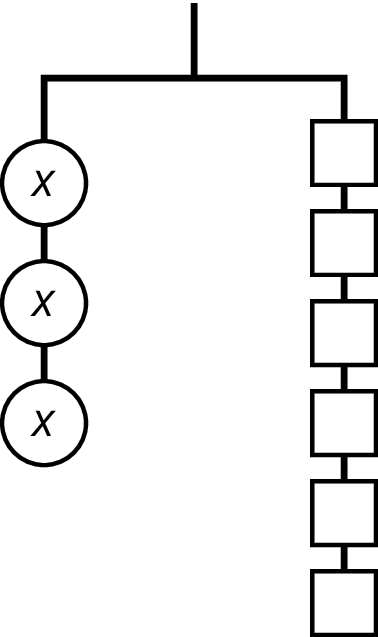
Balanced hanger. Left side, 3 identical circles labeled, x. Right side, 6 identical squares.
A:

\(x+x+x = 1+1+1+1+1+1\)

B:

\(x \boldcdot x \boldcdot x = 6\)

C:

\(3x = 6\)

D:

\(x + 3 = 6\)

E:

\(x \boldcdot x \boldcdot x = 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1\)

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Write an equation to represent each hanger.

Four balanced hangers, A, B, C, and D.

Solution

For access, consult one of our IM Certified Partners.

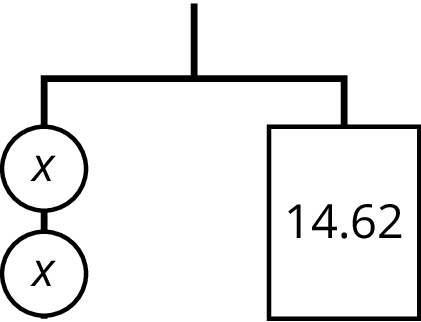
Problem 3

  1. Write an equation to represent the hanger.
     
  2. Explain how to reason with the hanger to find the value of \(x\).
     
  3. Explain how to reason with the equation to find the value of \(x\).
Balanced hanger. Left side, 2 identical circles, x, right side, 1 rectangle, 14 point 6 2. 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Andre says that \(x\) is 7 because he can move the two 1s with the \(x\) to the other side.

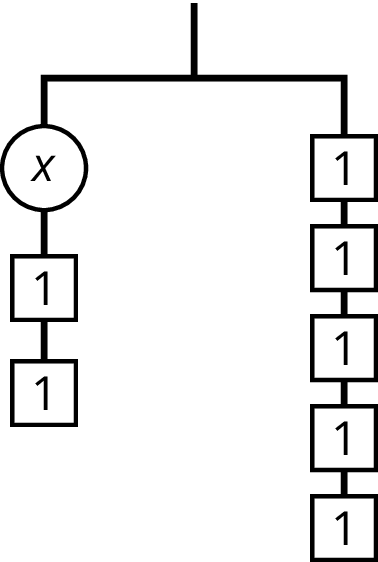
Balanced hanger. Left side, 1 circle, x, 2 identical squares, 1, right side, five identical squares, 1.

Do you agree with Andre? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Match each equation to one of the diagrams.

  1. \(12-m=4\)
  2. \(12=4\boldcdot m\)
  3. \(m-4=12\)
  4. \(\frac{m}{4}=12\)
Four tape diagrams labeled A, B, C, and D.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 6, Lesson 1.)

Problem 6

The area of a rectangle is 14 square units. It has side lengths \(x\) and \(y\). Given each value for \(x\), find \(y\).

  1. \(x=2\frac13\)
  2. \(x=4\frac15\)
  3. \(x=\frac76\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 13.)

Problem 7

Lin needs to save up $20 for a new game. How much money does she have if she has saved each percentage of her goal. Explain your reasoning.

  1. 25%
  2. 75%
  3. 125%

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 11.)