Lesson 15

Evaluate each expression if \(x=3\).

1. \(2^x\)
2. \(x^2\)
3. \(1^x\)
4. \(x^1\)
5. \(\left(\frac12\right)^x\)

Evaluate each expression for the given value of each variable.

1. \(2 + x^3\), \(x\) is 3 

2. \(x^2\), \(x\) is \(\frac{1}{2}\) 

3. \(3x^2+y\), \(x\) is 5 \(y\) is 3 

4. \(10y + x^2\), \(x\) is 6 \(y\) is 4

Decide if the expressions have the same value. If not, determine which expression has the larger value.

1. \(2^3\) and \(3^2\)

2. \(1^{31}\) and \(31^1\)

3. \(4^2\) and \(2^4\)

4. \(\left(\frac12\right)^3\) and \(\left(\frac13\right)^2\)

Match each equation to its solution.

An adult pass at the amusement park costs 1.6 times as much as a child’s pass.

1. How many dollars does an adult pass cost if a child’s pass costs:

   $5?

   $10?

   \(w\) dollars?

2. A child’s pass costs $15. How many dollars does an adult pass cost?

Jada reads 5 pages every 20 minutes. At this rate, how many pages can she read in 1 hour?

• Use a double number line to find the answer.

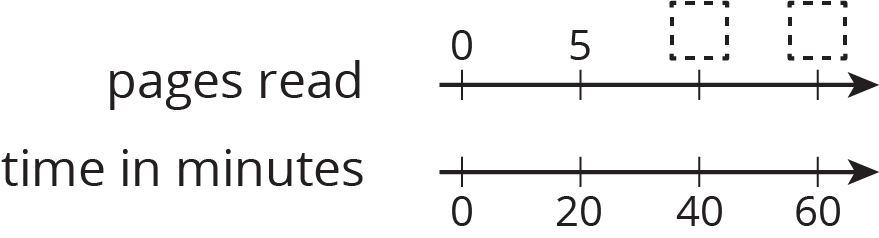
• Use a table to find the answer.

pages read	time in minutes
5	20

Which strategy do you think is better, and why?