Lesson 7
Equivalent Ratios Have the Same Unit Rates
7.1: Which One Doesn’t Belong: Comparing Speeds (10 minutes)
Warm-up
This warm-up prompts students to compare four rates. It encourages students to explain their reasoning, hold mathematical conversations, and gives you the opportunity to hear how they use terminology and talk about rates in comparison to one another. To allow all students to access the activity, each rate has one obvious reason it does not belong. During the discussion, listen for the term "unit rate," speed, pace, and ways that students reason about whether two rates indicate the same speed.
Launch
Arrange students in groups of 2–4. Display the rates for all to see. Ask students to indicate when they have noticed one that does not belong and can explain why. Give students 1 minute of quiet think time and then time to share their thinking with their small group. In their small groups, tell each student to share their reasoning why a particular question does not belong and together find at least one reason each question doesn't belong.
Student Facing
Which one doesn’t belong? Be prepared to explain your reasoning.
5 miles in 15 minutes
3 minutes per mile
20 miles per hour
32 kilometers per hour
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask each group to share one reason why a particular rate does not belong. Record and display the responses for all to see. After each response, ask the class if they agree or disagree. Since there is no single correct answer to the question of which one does not belong, attend to students’ explanations and ensure the reasons given are correct.
During the discussion, ask students to explain the meaning of any terminology they use, such as unit rate, speed, or pace. Also, press students on unsubstantiated claims.
7.2: Price of Burritos (10 minutes)
Activity
In a previous lesson about treadmill workouts, students calculated unit rates and identified ratios that have matching unit rates as equivalent (i.e., if \(\frac{a}{b}=\frac{c}{d}\), then \(a:b\) is equivalent to \(c:d\)). Here they make sense of this relationship from the other direction; they see that when two ratios are equivalent, they have the same unit rate (i.e., if \(a:b\) is equivalent to \(c:d\), then \(\frac{a}{b}=\frac{c}{d}\)).
Students explore the above by noticing structures in a table of equivalent ratios—that in addition to the values in the rows being equivalent ratios, the values in the columns have a multiplicative relationship (MP7). They see, specifically, that dividing the values of the two quantities in the ratio result in the same quotient—the associated unit rate—and that it can be used to reason about one quantity of the ratio when the other is known.
Students also begin to transition from numerical examples to encapsulating a relationship with variables as they generalize their observations above (MP8).
As students work and discuss, identify those who observed structures in the table and can describe them well. Also look for students who could explain how they know the per-item cost is the same given two ratios expressed in variables.
Launch
Arrange students in groups of 2. Give students a few minutes of quiet think time to complete the first two questions, and then 1–2 minutes to discuss with a partner their observations about the values in the table. Ask them to complete the last two questions together afterwards.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Design Principle(s): Optimize output (for justification)
Student Facing
- Two burritos cost $14. Complete the table to show the cost for 4, 5, and 10 burritos at that rate. Next, find the cost for a single burrito in each case.
number of burritos cost in dollars unit price
(dollars per burrito)2 14 4 5 10 \(b\) - What do you notice about the values in this table?
- Noah bought \(b\) burritos and paid \(c\) dollars. Lin bought twice as many burritos as Noah and paid twice the cost he did. How much did Lin pay per burrito?
number of burritos cost in dollars unit price
(dollars per burrito)Noah \(b\) \(c\) \(\frac{c}{b}\) Lin \(2 \boldcdot b\) \(2 \boldcdot c\) -
Explain why, if you can buy \(b\) burritos for \(c\) dollars, or buy \(2 \boldcdot b\) burritos for \(2 \boldcdot c\) dollars, the cost per item is the same in either case.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may not realize that the third column asks for dollars per 1 burrito and instead write 14 dollars per 2 burritos or 28 dollars per 8 burritos. If this happens, remind students that “per burrito” means “per 1 burrito.”
Activity Synthesis
After students have conferred with a partner, debrief as a class. Focus the discussion on students’ calculations and the relationships they noticed in the tables. Display a completed version of the first table for all to see. Select previously identified students to share their observations. As they explain, illustrate their comments on the table. Students may bring up that:
- The ratios shown in the first two columns are equivalent across all rows.
- The ratios in all rows have the same dollar-per-item value (unit rate).
- The value in the last column can be found by dividing the dollar amount by the number of burritos. (If students use phrasing such as, “divide the second column by the first column,” encourage them to use more precise terms (MP6).) Highlight the first two observations above, or bring them up if students do not. The last observation above is welcome but do not need to be emphasized as it will be the focus of the next activity.
Invite selected students to share their reasoning on the last two questions. Attend to the last question in particular, as it may be challenging to digest given its abstract nature. Consider using a double number line to help students visualize how the unit rate is the same for \(b : c\) and \(2b : 2c\), as shown.
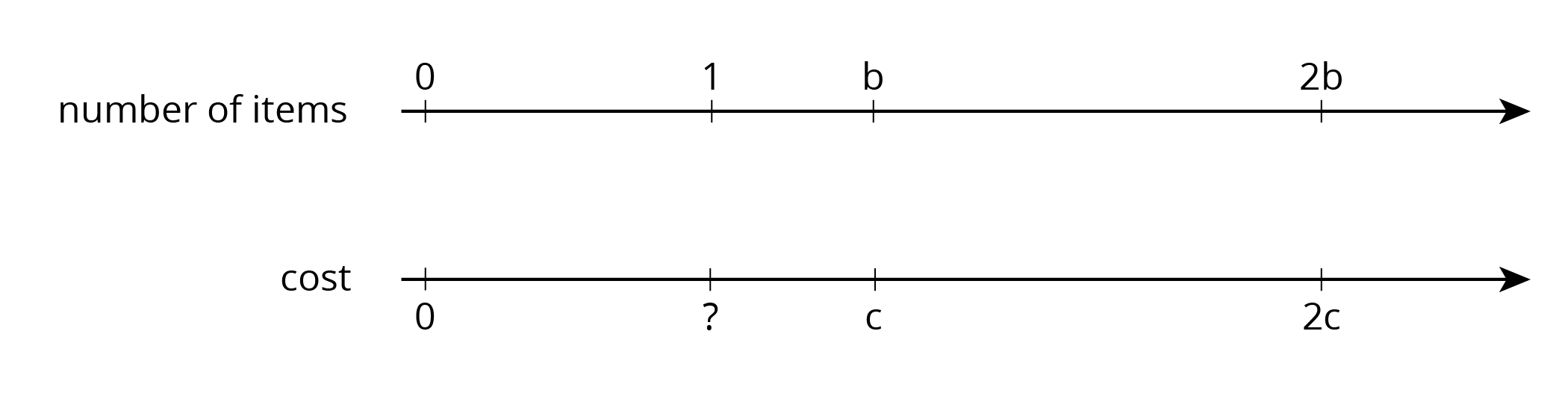
Connect the location of \(1:?\) with the unit rate, which students have by now recognized as having an unchanging value. Discuss how the unit rate is the same for any positive multiplier applied to \(b:c\), since the multiplier would produce equivalent ratios.
7.3: Making Bracelets (10 minutes)
Activity
At this point students understand that tables are a flexible tool for working with equivalent ratios. Up to this point, however, all actions performed on a table have started with both values of a known ratio \(a : b\) allowing students to move from row to row using multiplicative reasoning.
In this activity, however, students are asked to determine an unknown value of a ratio given only the other value of the ratio and a unit rate. Using their understanding of unit rate, equivalent ratios, and the relationship between the two (MP7), students learn how a unit rate is a factor that takes you from one column to another column in a table of equivalent ratios.
As students work, notice different approaches taken. For some students, the structure of the information in the table may not be apparent. Encourage them to refer to the tables in the preceding activity and think about the relationship between the ratios and unit rates there. Other students may be inclined to create a different table—such as the ones below—as an intermediate step for completing the given table. If so, consider asking them to share first during whole-class discussion.
| time in hours | number of bracelets | speed (bracelets per hour) |
|---|---|---|
| 1 | 6 | 6 |
| 2 | 12 | 6 |
This intermediate strategy makes good use of the “1” rows in the table, but is less efficient than directly dividing or multiplying by the unit rate to move from one column value to another since students have to work out both unit rates instead of using only the given unit rate.
Launch
Ask students to read the opening sentence and table. Explain that the first two columns show the ratio and the third column shows a unit rate associated with that ratio, similar to the structure of the tables in the previous activity.
Arrange students in groups of 2. Give students 3–4 minutes of quiet think time to complete the table and answer the questions, and then time to discuss their responses with a partner. Ask students to be mindful of how they go about completing the table and be prepared to explain their thinking.
Supports accessibility for: Social-emotional skills; Conceptual processing
Student Facing
- Complete the table. Then, explain the strategy you used to do so.
time in hours number of bracelets speed (bracelets per hour) 2 6 5 6 7 6 66 6 100 6 
-
Here is a partially filled table from an earlier activity. Use the same strategy you used for the bracelet problem to complete this table.
number of
burritoscost in
dollarsunit price
(dollars per burrito)14 7 28 7 5 7 10 7 - Next, compare your results with those in the first table in the previous activity. Do they match? Explain why or why not.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After they have a chance to discuss with a partner, select a few students to share with the class their strategies for completing the table. Start with students using less efficient strategies, such as those that worked out the 1 rows. Progress toward using the given unit rate to navigate from column to column in efficient ways, such as multiplying the time in hours by 6 to find number of bracelets, and multiplying the number of bracelets by \(\frac16\) to find time in hours.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
7.4: How Much Applesauce? (10 minutes)
Optional activity
This optional activity is a chance to apply more sophisticated, newly-learned techniques to a familiar-looking problem about equivalent ratios. None of the given numbers are multiples of each other from row to row (for example, 7 isn't a multiple of 4), so this problem lends itself to reasoning about unit rates.
Launch
If any student is familiar with making applesauce, ask them to explain how it is made. If not, explain: to make applesauce, you peel, core, and chop apples. Then, heat the apples gently in a saucepan for a while until they break down into a sauce. Finally, add flavors like lemon juice and cinnamon. If you know how many pounds of apples you start with, you can predict how many cups of applesauce after cooking.
Student Facing
It takes 4 pounds of apples to make 6 cups of applesauce.
-
At this rate, how much applesauce can you make with:
- 7 pounds of apples?
- 10 pounds of apples?
-
How many pounds of apples would you need to make:
- 9 cups of applesauce?
- 20 cups of applesauce?
| pounds of apples |
cups of applesauce |
|---|---|
| 4 | 6 |
| 7 | |
| 10 | |
| 9 | |
| 20 |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- Jada eats 2 scoops of ice cream in 5 minutes. Noah eats 3 scoops of ice cream in 5 minutes. How long does it take them to eat 1 scoop of ice cream working together (if they continue eating ice cream at the same rate they do individually)?
- The garden hose at Andre's house can fill a 5-gallon bucket in 2 minutes. The hose at his next-door neighbor’s house can fill a 10-gallon bucket in 8 minutes. If they use both their garden hoses at the same time, and the hoses continue working at the same rate they did when filling a bucket, how long will it take to fill a 750-gallon pool?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Highlight approaches where students compute how many pounds of apples per cup of applesauce and how many cups of applesauce per pound of apples and use multiplicative reasoning to move from column to column.
Design Principle(s): Support sense-making; Cultivate conversation
Lesson Synthesis
Lesson Synthesis
In this lesson, students learned about two new ideas around ratios and rates:
- Equivalent ratios have the same unit rate.
- Unit rates are the factors that take you from one column to the other column in a table of equivalent ratios.
Summarize for students the two new ideas and, if possible, highlight how students used them in the final activity of the lesson.
7.5: Cool-down - Cheetah Speed (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The table shows different amounts of apples selling at the same rate, which means all of the ratios in the table are equivalent. In each case, we can find the unit price in dollars per pound by dividing the price by the number of pounds.
| apples (pounds) |
price (dollars) |
unit price (dollars per pound) |
|---|---|---|
| 4 | 10 | \(10 \div 4 = 2.50\) |
| 8 | 20 | \(20 \div 8 = 2.50\) |
| 20 | 50 | \(50 \div 20 = 2.50\) |
The unit price is always the same. Whether we buy 4 pounds of apples for 10 dollars or 8 pounds of apples for 20 dollars, the apples cost 2.50 dollars per pound.
We can also find the number of pounds of apples we can buy per dollar by dividing the number of pounds by the price.
| apples (pounds) |
price (dollars) |
pounds per dollar |
|---|---|---|
| 4 | 10 | \(4 \div 10 = 0.4\) |
| 8 | 20 | \(8 \div 20 = 0.4\) |
| 20 | 50 | \(20 \div 50 = 0.4\) |
The number of pounds we can buy for a dollar is the same as well! Whether we buy 4 pounds of apples for 10 dollars or 8 pounds of apples for 20 dollars, we are getting 0.4 pounds per dollar.
This is true in all contexts: when two ratios are equivalent, their unit rates will be equal.
| quantity \(x\) | quantity \(y\) | unit rate 1 | unit rate 2 |
|---|---|---|---|
| \(a\) | \(b\) | \(\frac{a}{b}\) | \(\frac{b}{a}\) |
| \(s \boldcdot a\) | \(s \boldcdot b\) | \(\frac{s \boldcdot a}{s \boldcdot b} = \frac{a}{b}\) | \(\frac{s \boldcdot b}{s \boldcdot a} = \frac{b}{a}\) |