Lesson 16
Finding the Percentage
16.1: True or False: Percentages (10 minutes)
Warm-up
The purpose of this warm-up is to encourage students to reason about properties of operations in equivalent expressions. While students may evaluate each expression to determine if the statement is true or false, encourage students to think about the properties of arithmetic operations in their reasoning.
Launch
Display one problem at a time. Tell students to give a signal when they have decided if the equation is true or false. Give students 1 minute of quiet think time followed by a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Is each statement true or false? Be prepared to explain your reasoning.
- 25% of 512 is equal to \(\frac14 \boldcdot 500\).
- 90% of 133 is equal to \((0.9) \boldcdot 133\).
- 30% of 44 is equal to 3% of 440.
- The percentage 21 is of 28 is equal to the percentage 30 is of 40.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
- Do you agree or disagree? Why?
- Who can restate ___’s reasoning in a different way?
- Does anyone want to add on to _____’s reasoning?
After each true equation, ask students if they could rely on the same reasoning to determine if other similar problems are equivalent. After each false equation, ask students how the problem could be changed to make the equation true.
16.2: Jumping Rope (15 minutes)
Activity
The purpose of this activity is for students to see that to find what percentage one number is of another, divide them and then multiply by 100. First they find what percentage of 20 various numbers are, then they organize everything into a table. Using the table, students then describe the relationship they see between dividing the numbers by 20 and finding the percentage (MP8).
Launch
Depending on students' strengths in grade 5 work, it may be beneficial to offer some strategies for writing a fraction in an equivalent decimal form before students start working. Display the fraction \(\frac{15}{25}\) and ask students how they might think about writing it in decimal form. Possible strategies are writing the equivalent fraction \(\frac{60}{100}\) and knowing that "60 hundredths" is written 0.60 or 0.6. Another possibility is to write the equivalent fraction \(\frac35\), which is equal to \(\frac{6}{10}\) and knowing that "6 tenths" can be written as 0.6.
Give students quiet think time to complete the activity and then time to share their explanations with a partner.
Supports accessibility for: Language; Conceptual processing
Design Principle(s): Support sense-making, Optimize output (for explanation)
Student Facing
A school held a jump-roping contest. Diego jumped rope for 20 minutes.
-
Jada jumped rope for 15 minutes. What percentage of Diego’s time is that?
-
Lin jumped rope for 24 minutes. What percentage of Diego’s time is that?
-
Noah jumped rope for 9 minutes. What percentage of Diego’s time is that?
- Record your answers in this table. Write the quotients in the last column as decimals.
time (minutes) percentage \(\text{time} \div 20\) Diego 20 100 \(\frac{20}{20} = 1\text{ }\) Jada 15 \(\frac{15}{20} = \text{ }\) Lin 24 \(\frac{24}{20} = \text{ }\) Noah 9 \(\frac{9}{20} = \text{ }\) - What do you notice about the numbers in the last two columns of the table?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Have students share their strategies for the first three problems. Then ask what they noticed about the last two columns. There are many ways to formulate the relationship. Make sure everyone sees that to find what percentage a number is of 20, divide it by 20 and then multiply by 100. A table showing the percentage for 1 minute might also help:
| time (minutes) | percentage | |
|---|---|---|
| Diego | 20 | 100 |
| unit rate | 1 | 5 |
| Jada | 15 | 75 |
| Lin | 24 | 120 |
| Noah | 9 | 45 |
Note that to find the percentage for 1 minute, we divide 100 by 20, and to find the percentage for any number of minutes, we multiply the result by that number of minutes. That is the same as dividing the number of minutes by 20 and multiplying by 100.
16.3: Restaurant Capacity (10 minutes)
Activity
This activity gives students a chance to practice their new-found insight about how to find percentages. It also gives them an opportunity to practice dividing whole numbers in preparation for the next unit on base-ten numbers.
Note that it is expected and perfectly okay for students to revert to less-efficient methods that they trust. Monitor for students with more- and less-efficient methods. A less-efficient representation can be used to make sense of a more-efficient method, and these connections can be made in the discussion that follows the task.
Launch
Give students quiet think time to complete the activity and then time to share their explanations with a partner.
Supports accessibility for: Language; Organization
Student Facing
A restaurant has a sign by the front door that says, “Maximum occupancy: 75 people.” Answer each question and explain or show your reasoning.
- What percentage of its capacity is 9 people?
- What percentage of its capacity is 51 people?
- What percentage of its capacity is 84 people?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Water makes up about 71% of Earth’s surface, while the other 29% consists of continents and islands. 96% of all Earth’s water is contained within the oceans as salt water, while the remaining 4% is fresh water located in lakes, rivers, glaciers, and the polar ice caps.
If the total volume of water on Earth is 1,386 million cubic kilometers, what is the volume of salt water? What is the volume of fresh water?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share various approaches to the three problems. Sequence less-efficient methods before more-efficient ones. Make sure all students have a chance to see the approach that is the focus of this lesson. For example, to find "9 is what percent of 75?" we can divide 9 by 75 and then multiply by 100.
Design Principles(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
The main idea in this lesson is that to find what percentage \(C\) is of \(B\), multiply: \(\displaystyle \frac{C}{B} \boldcdot 100\) Ask students to describe a procedure for finding what percentage one number is of another number. If they struggle to describe a general method, ask about some specific examples, like “How could you find what percentage of 80 is 56?” (You could multiply 100 by \(\frac{56}{80}\).)
16.4: Cool-down - Jet Fuel (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
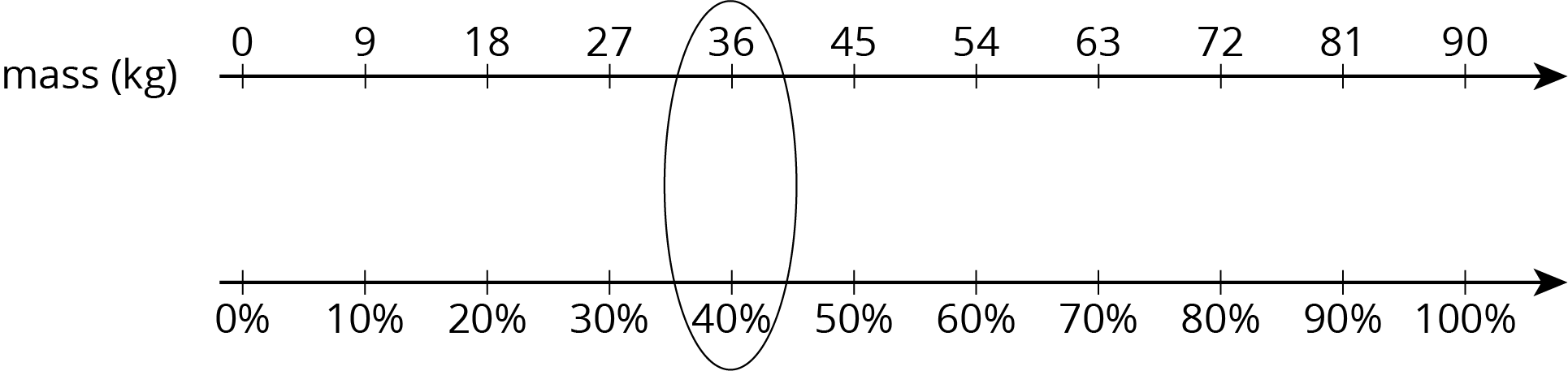
What percentage of 90 kg is 36 kg? One way to solve this problem is to first find what percentage 1 kg is of 90, and then multiply by 36.
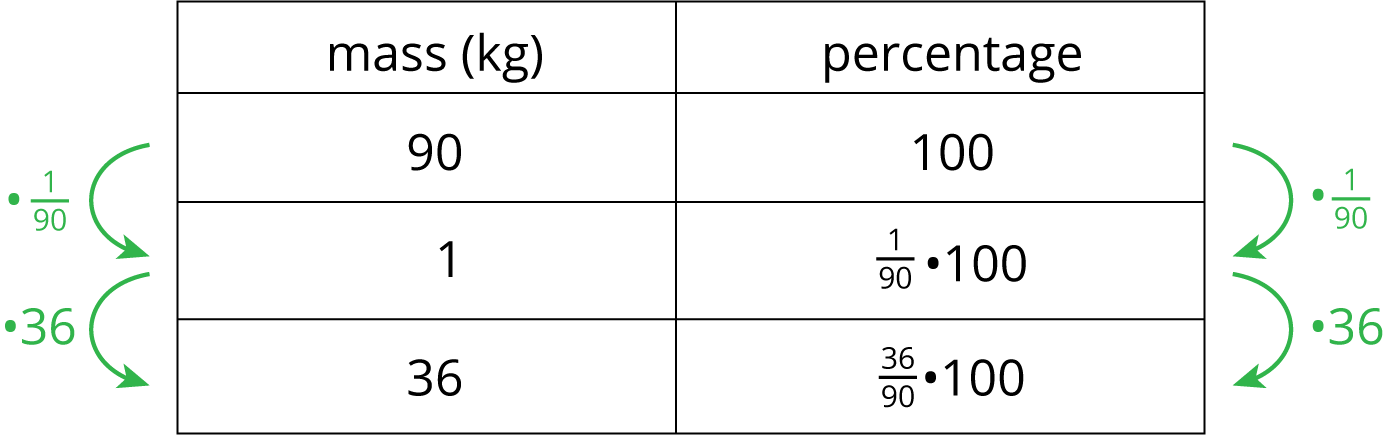
From the table we can see that 1 kg is \(\left(\frac{1}{90}\boldcdot 100\right) \%\), so 36 kg is \(\left(\frac{36}{90}\boldcdot 100\right) \%\) or 40% of 90. We can confirm this on a double number line:
In general, to find what percentage a number \(C\) is of another number \(B\) is to calculate \(\frac{C}{B}\) of 100%. We can find that by multiplying: \(\displaystyle \frac{C}{B}\boldcdot 100 \)
Suppose a school club has raised \$88 for a project but needs a total of \$160. What percentage of its goal has the club raised?
To find what percentage \$88 is of \$160, we find \(\frac {88}{160}\) of 100% or \(\frac {88}{160} \boldcdot 100\), which equals \( \frac {11}{20} \boldcdot 100\) or 55. The club has raised 55% of its goal.