Lesson 14
Solving Percentage Problems
14.1: Number Talk: Multiplication with Decimals (10 minutes)
Warm-up
This number talk encourages students to rely on what they know about structure, patterns, decimal multiplication, and properties of operations to solve a problem mentally. Only two problems are given here so there is time to share many strategies and make connections between them.
Launch
Display one problem at a time. Give students 1 minute of quiet think time per problem, and ask students to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find the products mentally.
\(6\boldcdot (0.8)\boldcdot 2\)
\((4.5)\boldcdot (0.6)\boldcdot 4\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their explanations for all to see. If not mentioned by students, ask if or how the given factors impacted their strategy choice. To involve more students in the conversation, consider asking:
- Who can restate ___’s reasoning in a different way?
- Did anyone solve the problem the same way but would explain it differently?
- Did anyone solve the problem in a different way?
- Does anyone want to add on to _____’s strategy?
- Do you agree or disagree? Why?
Design Principle(s): Optimize output (for explanation)
14.2: Coupons (10 minutes)
Activity
In this activity, students solve percentage problems in the context of shopping. Students consider how discounts described as percentages translate into reduced prices and the other way around. (In other words, they find \(A\) and \(C\) where \(A\%\) of \(B\) is \(C\)). In each problem, students need to first determine what value is associated with 100% and reason accordingly.
Students may choose to use double number lines or tables or simply reason without using a particular representation. For instance, to find 10% of $15 they may first find 50% by dividing $15 by 2, and then divide the resulting $7.50 by 5 to obtain 10% of $15. Those who have internalized the structure of percentages may be able to multiply or divide even more efficiently (e.g., \(15 \boldcdot \frac{1}{10} = 1.5\), or \(15 \div 10 = 1.5\)). These strategies will be investigated more in the next lesson. For now, encourage students to also explain their reasoning with a double number line or table.
As students work, identify students who use different strategies so that they can share later.
Launch
Display some coupons for all to see. Point out that some coupons specify amounts to be taken off in dollars (e.g., $5 off) and some specify percentages (e.g.,10% off). Tell students that they will solve a couple of shopping problems that involve discounts.

Give students quiet think time to complete the activity and then time to share their explanation with a partner.
Supports accessibility for: Language; Social-emotional skills
Student Facing
Han and Clare go shopping, and they each have a coupon. Answer each question and show your reasoning.
-
Han buys an item with a normal price of $15, and uses a 10% off coupon. How much does he save by using the coupon?

- Clare buys an item with a normal price of $24, but saves $6 by using a coupon. For what percentage off is this coupon?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Clare paid full price for an item. Han bought the same item for 80% of the full price. Clare said, “I can’t believe I paid 125% of what you paid, Han!” Is what she said true? Explain.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Since the first question asks students to find the dollar amount, some students may think that $6 is the answer to the second question and not realize that it is asking them to find the percentage. Also, some students may try to find the sale price on the first question and the percentage of the sale price on the second question, instead of the discount and the percentage of the discount. Encourage them to revisit the questions or clarify what the questions ask.
Activity Synthesis
Select students who used different representations: first a tape diagram, then a double number line or a table (or both, time permitting). As students explain, illustrate and display those representations for all to see. If no students mention using a double number line or a table, demonstrate at least one of these methods. When discussing double number lines (or tables), ask students if the same double number line (or table) could be used to solve both problems and discuss why not. Emphasize the fact that two separate double number lines (or tables) are necessary because the value for 100% is different in each case.
Design Principles(s): Cultivate conversation; Maximize meta-awareness
14.3: Info Gap: Music Devices (20 minutes)
Activity
In this info gap activity, students find both \(A\) and \(C\) (where \(A\%\) of \(B\) is \(C\)) in the context of buying a music device. The value of \(B\) is different in each of the two questions about the music device, so students who choose to draw diagrams or tables need to draw two. When answering the second question—expressing \$24 as a percentage of \$25—students may notice that drawing a complete double number line diagram with all 25 tick marks is rather time consuming. Encourage students to look for and make use of any noticeable structure (MP7) or pattern (MP8) to help them solve more efficiently.
Some students may, for example, see that if \$25 corresponds to 100%, then each dollar—and thus each tick mark—is \(100 \div 25\) or 4. They can then bypass drawing the rest of the tick marks and simply multiply \(4 \boldcdot 24\) to obtain 96. Some may notice that \$24 is \$1 away from \$25 and simply subtract the corresponding percentage from 100% (\(100 - 4 = 96\)). A table provides another efficient structure for reasoning about this. Monitor for students who use different strategies.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Here is the text of the cards for reference and planning:

Note: If time is short, the second set of cards can be considered optional. It would be better for students to thoroughly understand one of these problems than to rush through both of them with less understanding.
Launch
Arrange students in groups of 2. In each group, distribute the first problem card to one student and a data card to the other student. After debriefing on the first problem, distribute the cards for the second problem, in which students switch roles.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students with different strategies to share their approaches to the first question, starting with less efficient methods and ending with more efficient methods. Then, ask the class to predict how the same strategies might be used to solve the second question, and how the second problem could be solved more quickly.
Lesson Synthesis
Lesson Synthesis
We know that 20% of 400 liters is 80 liters. There are three different questions we can ask:
- What is 20% of a 400 liter tank?

- 20% of a full tank is 80 liters. How many liters are in a full tank?

- 80 liters is what percentage of a 400 liter tank?
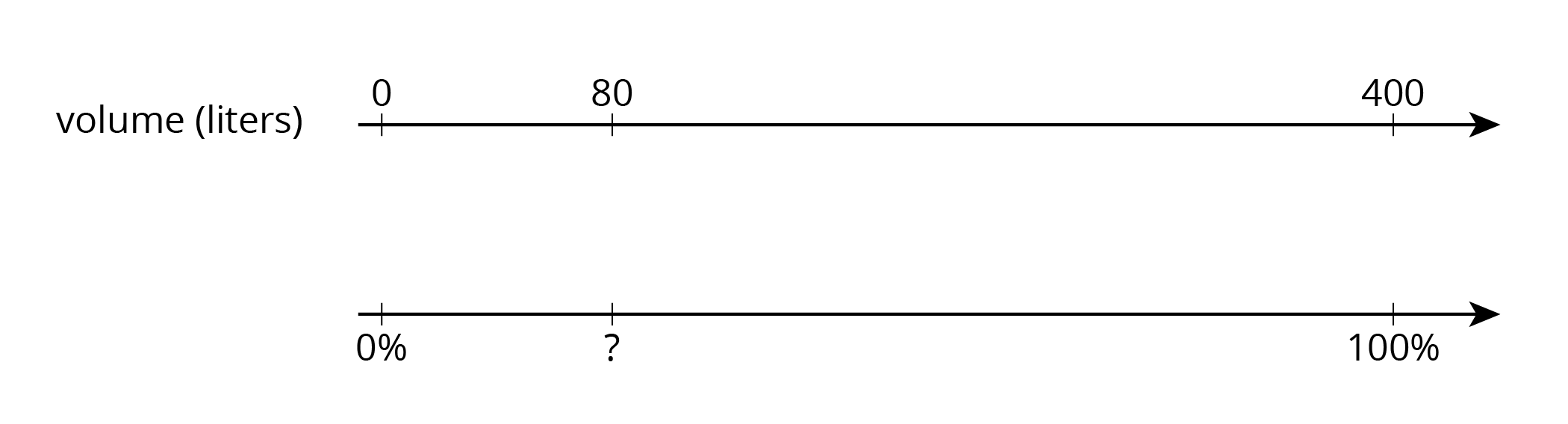
We can use a double number line to answer all three of these questions. In a previous lesson, we learned how to solve the first two kinds of problems. In this lesson, we also addressed the third kind of problem. We can begin solving by asking ourselves: what fraction of 400 is 80? The answer can tell us how many tick marks to place on the number line or how to divide the segment between 0 and 100%. \(80 \div 400 = \frac15\), so we can divide segment between 0 and 100% into five equal parts, as shown here:
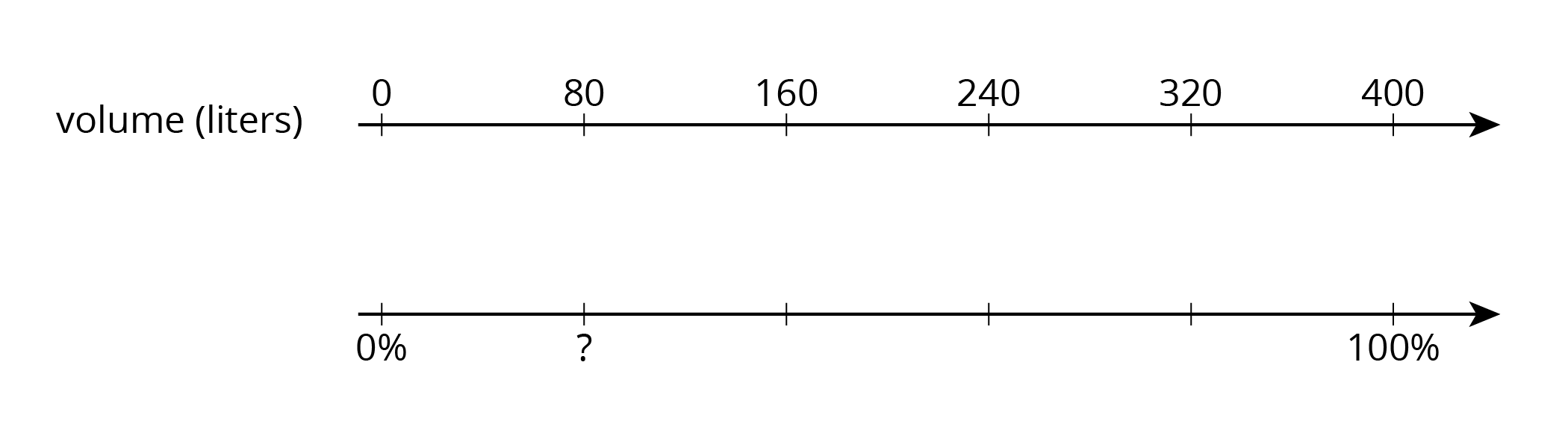
Since \(\frac15\) of 100 is 20, we know the percentage is 20. We can also use a table:
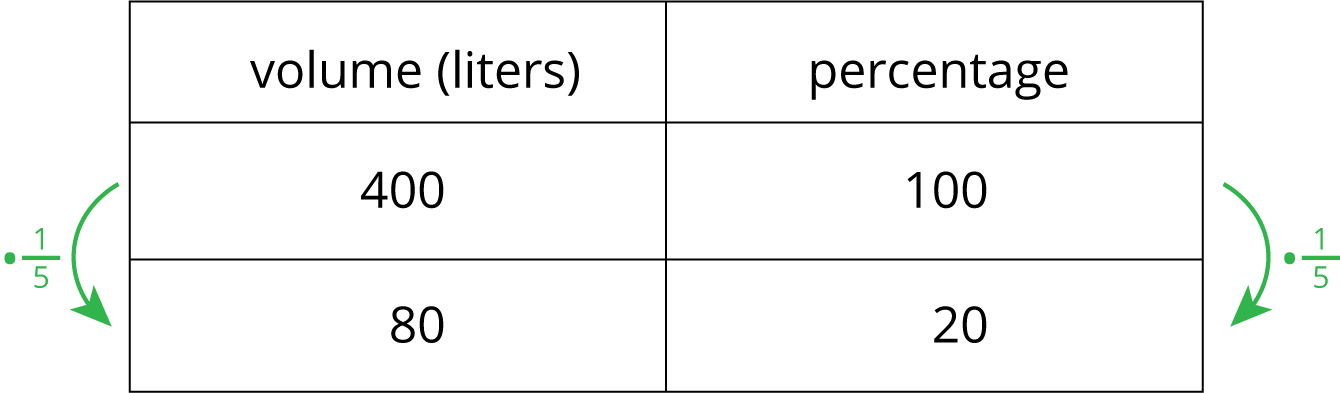
14.4: Cool-down - Walking to School (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
A pot can hold 36 liters of water. What percentage of the pot is filled when it contains 9 liters of water?
Here are two different ways to solve this problem:
-
Using a double number line:

We can divide the distance between 0 and 36 into four equal intervals, so 9 is \(\frac14\) of 36, or 9 is 25% of 36.
- Using a table:
