Lesson 9
Solving Rate Problems
9.1: Grid of 100 (5 minutes)
Warm-up
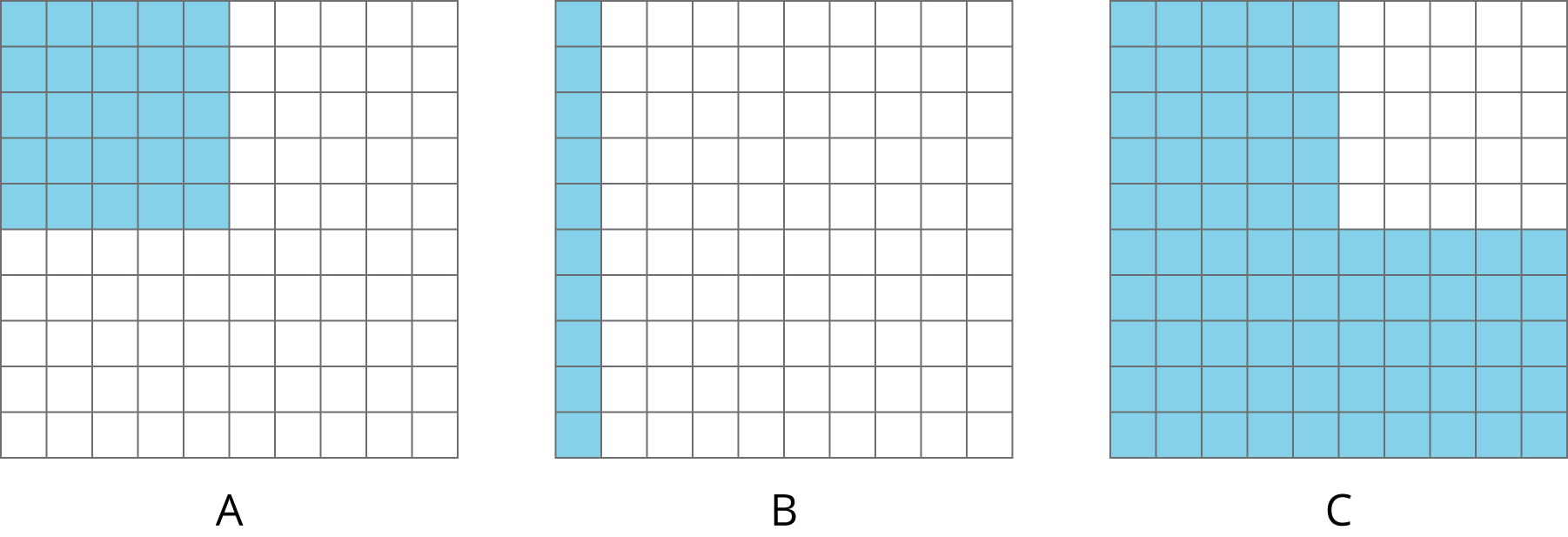
In this warm-up, students are asked to name the shaded portion of a 10-by-10 grid, which is equal to 1. To discourage students from counting every square, flash the image for a few seconds and then hide it. Flash it once more for students to check their thinking. Ask, “How did you see the shaded portion?” instead of “How did you solve for the shaded portion?” so students can focus on the structure of the fractional pieces and tenths in the image. Encourage students to name the shaded portion in fractions or decimals. Some students may also bring up percentages.
Launch
Tell students you will show them a 10 x 10 grid for 3 seconds and that the entire grid represents 1. Their job is to find how much is shaded in the image and explain how they saw it.
Display the image for 3 seconds and then hide it. Do this twice. Give students 15 seconds of quiet think time between each flash of the image. Encourage students who have one way of seeing the grid to consider another way to determine the size of the shaded portion while they wait.
Student Facing
How much is shaded in each one?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share how they visualized the shaded portion of each image. Record and display their explanations for all to see. Solicit from the class alternative ways of quantifying the shaded portion and alternative ways of naming the size of the shaded portion (to elicit names in fractions, decimals, and percentages). To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone solve the shaded portion the same way but would explain it differently?”
- “Did anyone solve the shaded portion in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
9.2: Card Sort: Is it a Deal? (20 minutes)
Activity
Students are given cards, each of which contains an original price and a new price, as shown.
|
B. Juice Boxes Original: 10 for \$3.50 New Deal: 6 for \$2.40 |
Their job is to sort the cards into two piles: one pile for deals they would take, and another for those they would reject. There are many paths students could use to reason about whether or not to accept a deal. For example, if the original deal was \$3.50 for 10 juice boxes and the new deal is \$2.40 for 6 juice boxes, they could:
-
Find and compare the unit rates for both the original pack and the new pack. If the unit rate is the same, the deal is fair. If the unit rate is lower, the clerk is offering a discount. If the unit rate is higher, the clerk is not being fair.
number of juice boxes cost in dollars dollars per box 10 3.50 0.35 6 2.40 0.40 -
Find the unit rate in the original pack, apply it to the number of items in the new pack, and compare the costs for the same number of items in the original and new pricing schemes. This can be done in two ways, one focused more on column reasoning and the other on row reasoning, as shown.
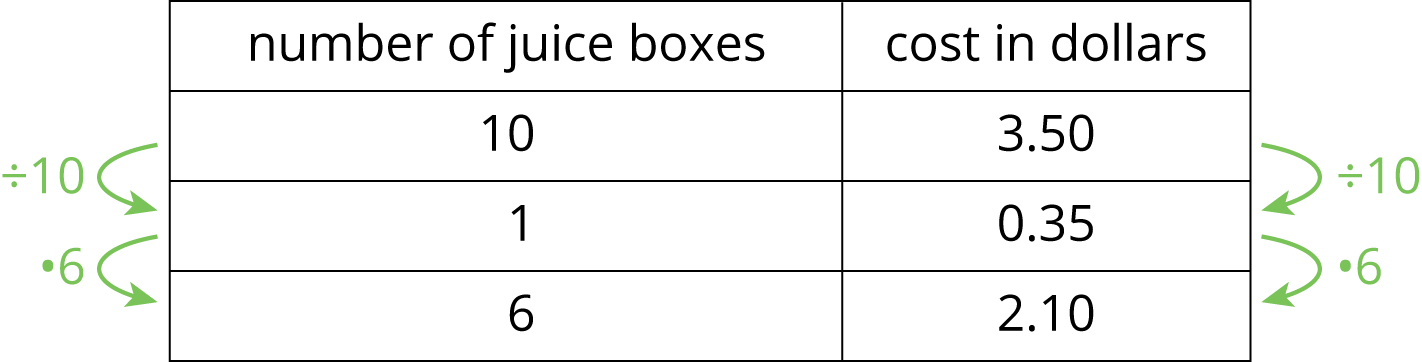
- Use an abbreviated table and bypass calculating the unit rate. Find the multiplier to get from the original to the new number of items, and use the same multiplier to find what the price would be if the deal has not changed. Compare the actual new price to this projected price.

As students work, attend to how they reason about the deals and make their decisions (deal or no deal).
Launch
Show the picture on Card A (or use an actual 4-pack of a beverage with a missing bottle.) Present the following situation:
“You’ve entered a local shop to buy a 4-pack of drinks. You find one last pack of the drink you want on the shelf and, unfortunately, only 3 bottles remain in that pack. You decide to buy it anyway. You take the 3-pack to the check-out counter and ask the clerk to consider a fair price for the incomplete pack. If the cost of a 4-pack was $3.16 and the clerk offers to sell the 3 pack for $2.25, will you take the deal?”
Poll the class for their response and display how many students would and would not take the deal. Then, ask “How could you figure out if the deal is good or not?” Give students a moment of quiet think time to come up with strategies for solving such a problem and then invite a few students to share.
Arrange students in groups of 2. Give each group a set of five cards A–E (or six cards A–F if including the extension problem). Tell students their job is to sort the cards into a ‘Deal’ pile and a ‘No Deal’ pile. Instruct partners to collaborate in finding the answer for card A and divide up the remaining cards between them. Ask students to first work on their cards individually, then share their reasoning with their partner, and lastly, sort the cards together.
Supports accessibility for: Conceptual processing; Organization
Student Facing
Your teacher will give you a set of cards showing different offers.
- Find card A and work with your partner to decide whether the offer on card A is a good deal. Explain or show your reasoning.
-
Next, split cards B–E so you and your partner each have two.
- Decide individually if your two cards are good deals. Explain your reasoning.
- For each of your cards, explain to your partner if you think it is a good deal and why. Listen to your partner’s explanations for their cards. If you disagree, explain your thinking.
- Revise any decisions about your cards based on the feedback from your partner.
- When you and your partner are in agreement about cards B–E, place all the cards you think are a good deal in one stack and all the cards you think are a bad deal in another stack. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Time to make your own deal! Read the information on card F and then decide what you would charge if you were the clerk. When your teacher signals, trade cards with another group and decide whether or not you would take the other group’s offer.
Keep in mind that you may offer a fair deal or an unfair deal, but the goal is to set a price close enough to the value it should be that the other group cannot immediately tell if the deal you offer is a good one.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students who are not fluent in multiplication and division computation work from grade 5 may need some review in order to be successful in this activity.
Activity Synthesis
Select 2–3 students who used different but effective strategies to share their thinking with the class. Encourage students to listen to others’ reasoning. Record the different strategies in one place and display them for all to see. Highlight any similarities and differences (e.g., whether a unit rate was used, whether students compare the original unit rate to the new quantity or the other way around, etc.)
Design Principle(s): Support sense-making; Maximize meta-awareness
9.3: The Fastest of All (15 minutes)
Activity
In this activity, students convert between customary and metric units in order to compare lengths. To make some measurements comparable to others, students need to perform multistep conversions and activate arithmetic skills from previous grades. Support students with computations as needed and provide access to calculators as appropriate. Share the following information with students when requested.
- 1 mile = 1,760 yards = 5,280 feet
- 1 yard = 3 feet
- 1 foot = 12 inches
- 1 kilometer = 1,000 meters
- 1 meter = 100 centimeters
Expect students to choose different units of measurements to make comparisons. As students work, identify those who opt for the same unit so that they can partnered or grouped together for discussion.
Launch
Give students 1–2 minutes to read the task, and then ask how they think they could compare these lengths. Students are likely to suggest converting all the lengths into the same unit of measurement. Ask students which units might be appropriate in this case and why. (Feet, yards, and meters are better choices than inches or miles.) After discussing some appropriate options, give students quiet think time to complete the activity, and then time to share their explanation with one or more students who have chosen to use the same unit of measurement.
Supports accessibility for: Memory; Organization
Student Facing
Wild animals from around the world wanted to hold an athletic competition, but no one would let them on an airplane. They decided to just measure how far each animal could sprint in one minute and send the results to you to decide the winner.
You look up the following information about converting units of length:
1 inch = 2.54 centimeters
| animal | sprint distance |
|---|---|
| cougar | 1,408 yards |
| antelope | 1 mile |
| hare | 49,632 inches |
| kangaroo | 1,073 meters |
| ostrich | 1.15 kilometers |
| coyote | 3,773 feet |
- Which animal sprinted the farthest?
-
What are the place rankings for all of the animals?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may need to be prompted about the intermediate steps needed to compare units that require several conversions before they can be compared.
Activity Synthesis
Poll the class to see if they agree on who took first, second, third, and last place. If there is widespread agreement, invite two students to share: one student who converted all measurements to feet or yards, and another who converted everything to meters. If there are discrepancies, list the distances run by each animal in each unit of measurement and display them for all to analyze and double check. While the numerical values of the measurements in feet will all be greater than those in meters, the rank order will come out the same.
Design Principle(s): Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Emphasize that when we want to compare rates, a straightforward way is to compare unit rates. For example, when we were comparing the best deal, an example was 10 juice boxes for \$3.50 or 6 juice boxes for \$2.40. It may be helpful to draw two tables or two double number lines to facilitate discussion. Questions to discuss:
- “What are two associated unit rates that we could compare?” (0.35 and 0.4)
- “How were they computed?” (Divide 3.5 by 10 and divide 2.4 by 6)
- “What do these numbers mean in this context?” (They are each the price per bottle for the different offers. For example, \$0.35 for 1 bottle.)
9.4: Cool-down - Tacos by the Pack (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Sometimes we can find and use more than one unit rate to solve a problem.
Suppose a grocery store is having a sale on shredded cheese. A small bag that holds 8 ounces is sold for \$2. A large bag that holds 2 kilograms is sold for \$16. How do you know which is a better deal?
Here are two different ways to solve this problem:
Compare dollars per kilogram.
- The large bag costs \$8 per kilogram, because \(16 \div 2 = 8\).
-
The small bag holds \(\frac12\) pound of cheese, because there are 16 ounces in 1 pound, and \(8 \div 16 = \frac12\).
The small bag costs \$4 per pound, because \(2 \div \frac12 = 4\). This is about \$8.80 per kilogram, because there are about 2.2 pounds in 1 kilogram, and \(4.00 \boldcdot 2.2 = 8.80\).
The large bag is a better deal, because it costs less money for the same amount of cheese.
Compare ounces per dollar.
- With the small bag, we get 4 ounces per dollar, because \(8 \div 2 = 4\).
-
The large bag holds 2,000 grams of cheese. There are 1,000 grams in 1 kilogram, and \(2 \boldcdot 1,\!000 = 2,\!000\). This means 125 grams per dollar, because \(2,\!000 \div 16 = 125\).
There are about 28.35 grams in 1 ounce, and \(125 \div 28.35 \approx 4.4\), so this is about 4.4 ounces per dollar.
The large bag is a better deal, because you get more cheese for the same amount of money.
Another way to solve the problem would be to compare the unit prices of each bag in dollars per ounce. Try it!