Lesson 15
Finding This Percent of That
15.1: Number Talk: Decimals (5 minutes)
Warm-up
The purpose of this number talk is to help students multiply and divide decimal numbers by 100 in preparation for their work with percentages later in the lesson.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time for each problem, and ask them to give a signal when they have an answer and a strategy. Keep all previous problems displayed throughout the task.
Supports accessibility for: Memory; Organization
Student Facing
Find the value of each expression mentally.
\((0.23) \boldcdot 100\)
\(50 \div 100\)
\(145 \boldcdot \frac{1}{100}\)
\(7 \div 100\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select a couple of students to share their answer and strategies for each problem. Record and display their explanations for all to see. After evaluating all four expressions, ask students:
- How is multiplying by \(\frac{1}{100}\) related to division?
- What is important to remember about dividing a one digit number by 100?
To involve more students in the conversation, consider asking as the students share their ideas:
- Who can restate ___’s reasoning in a different way?
- Did anyone solve the problem the same way but would explain it differently?
- Did anyone solve the problem in a different way?
- Does anyone want to add on to _____’s strategy?
- Do you agree or disagree? Why?
Design Principle(s): Optimize output (for explanation)
15.2: Audience Size (15 minutes)
Activity
In this activity, students encounter percentage problems that are inconvenient to solve by drawing double number lines, encouraging them to reason differently and begin noticing that \(P\%\) of a number is \(\frac{P}{100}\) times that number.
The first two questions, which ask students to find 30% and 140% of some values, can be solved using a familiar percentage,10%, as a stepping stone. For example, to solve for 30% of 250, students may find 10% or \(\frac{1}{10}\) of 250 and then multiply the result by 3. This intermediate percentage does not work well for the last question, however, prompting them to find a workaround.
Students may resort to using a double number line, but may soon find it impractical. For example, they may decide to divide by 100% into 25 parts to find the value of 4%, which they can then multiply by 11. As time consuming drawing 25 tick marks is, it may encourage students to look for structure that may open a shorter path to the solution. For example, once they know that they need tickmarks every 4% and every 10 people, they can bypass the rest of the tick marks and multiply (\(4 \boldcdot 11 = 44\) and \(10 \boldcdot 11 = 110\)) to find that 110 people attended literacy night.
Others may see that dividing the given value by 100 to find the value of 1% and then multiplying the result by the targeted percentage works well. Identify students who take this path so they can share later.
Launch
Give students quiet think time to complete the activity and then time to share their explanation with a partner.
Supports accessibility for: Organization; Attention
Student Facing
A school held several evening activities last month—a music concert, a basketball game, a drama play, and literacy night. The music concert was attended by 250 people. How many people came to each of the other activities?
- Attendance at a basketball game was 30% of attendance at the concert.
- Attendance at the drama play was 140% of attendance at the concert.
- Attendance at literacy night was 44% of attendance at the concert.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
50% of the people who attended the drama play also attended the music concert. What percentage of the people who attended the music concert also attended the drama play?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite a couple of students to share their work on the first two questions, but focus the whole-class discussion on the last one. Select several students who effectively found 44% of 250 to share, saving the strategy involving 1% for last. If no one used this method, illustrate and explain it. Consider using a table in doing so, as shown below.
| people | percentage |
|---|---|
| 250 | 100 |
| 2.5 | 1 |
| 110 | 44 |
Guide students to see that this method of finding percentages can be generalized across all such problems, much like finding a unit rate is an effective way to solve any ratio problem.
Design Principles(s): Cultivate conversation; Maximize meta-awareness
15.3: Everything is On Sale (15 minutes)
Activity
In general, \(P\%\) of something is \(\frac{P}{100}\) times that thing. The purpose of this activity is to make this explicit. In this activity, students are asked to find 80% of several different values, generalize their process, and express their generalization in different ways. As they make repeated calculations, students look for and express regularity in their work (MP8) and see more explicitly that \(P\%\) of a number is \(\frac{P}{100}\) times that number. Once they arrive at one or more generalizations, students practice articulating why each generalization always works (MP3).
Launch
Give students quiet think time to complete the activity and then time to share their explanation with a partner.
Supports accessibility for: Memory; Conceptual processing
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
During a sale, every item in a store is 80% of its regular price.
- If the regular price of a T-shirt is $10, what is its sale price?
- The regular prices of five items are shown here. Find the sale price of each item.
item 1 item 2 item 3 item 4 item 5 regular price $1 $4 $10 $55 $120 sale price -
You found 80% of many values. Was there a process you repeated over and over to find the sale prices? If so, describe it.
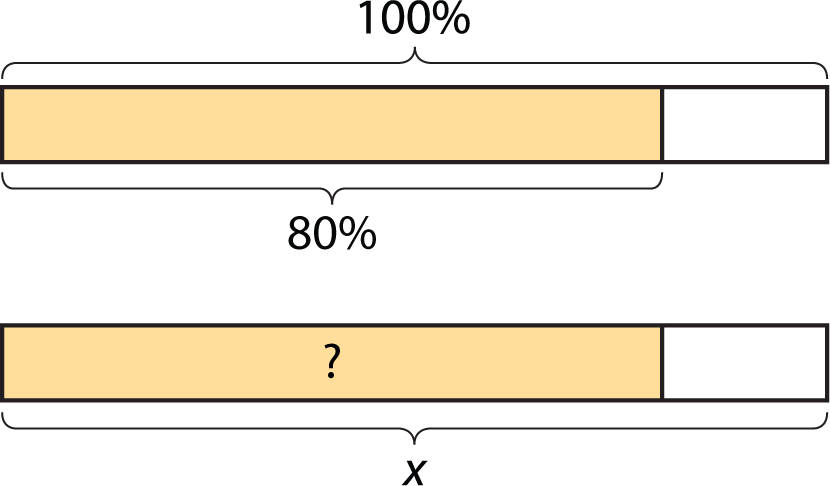
-
Select all of the expressions that could be used to find 80% of \(x\). Be prepared to explain your reasoning.
\(\frac{8}{100} \boldcdot x\)
\(\frac{80}{100} \boldcdot x\)
\(\frac{8}{10} \boldcdot x\)
\(\frac{4}{10} \boldcdot x\)
\(\frac85 \boldcdot x\)
\(\frac45 \boldcdot x\)
\(80 \boldcdot x\)
\(8 \boldcdot x\)
\((0.8) \boldcdot x\)
\((0.08) \boldcdot x\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Make sure students have the correct values in the table for the second question. Then, discuss the expressions, starting with \(\displaystyle \frac{80}{100} \boldcdot x.\)
Guide students to see that if we know the value of 100%, dividing that value by 100 (or equivalently, multiplying it by \(\frac{1}{100}\)) tells us the corresponding value for 1%. We can then multiply that value by the desired percentage. Consider using a table to organize this argument, as shown below:
| percentage | regular price |
|---|---|
| 100 | \(x\) |
| 1 | \(\frac{1}{100} \boldcdot x\) |
| 80 | \(\frac{80}{100} \boldcdot x\) |
After everyone understands where this expression comes from, ask students to discuss the remaining expressions with a partner. This is a good opportunity for just-in-time review on equivalent fractions, if needed.
Lesson Synthesis
Lesson Synthesis
The main idea in this lesson is that to find \(P\%\) of \(x\), multiply: \(\displaystyle \frac{P}{100} \boldcdot x\) Ask students to describe a procedure for finding a percent of a number. If they struggle to describe a general method, ask about some specific examples, like “How could you find 32% of 500?” (You could multiply 500 by \(\frac{32}{100}\).)
15.4: Cool-down - Ordering Percentages of Different Numbers (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To find 49% of a number, we can multiply the number by \(\frac{49}{100}\) or 0.49.
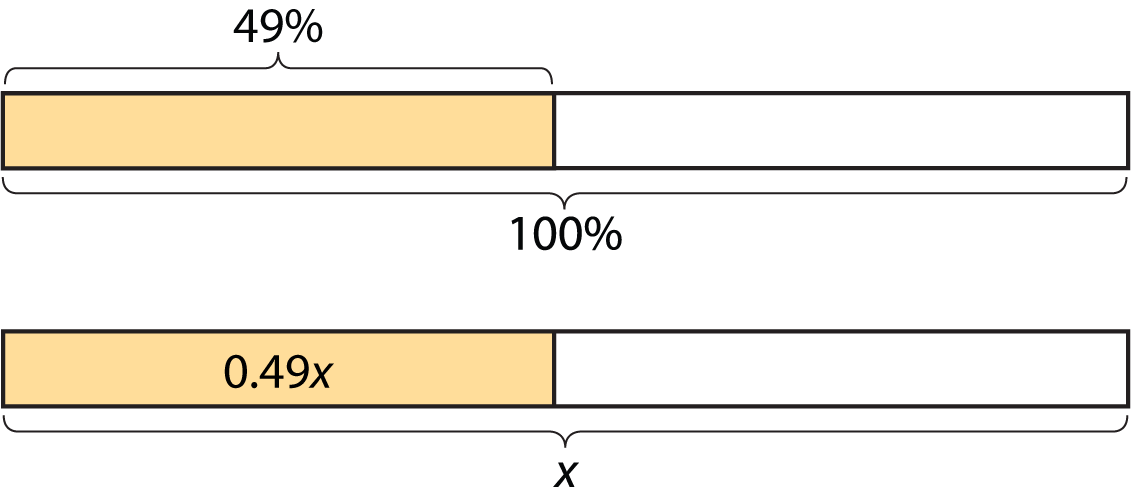
To find 135% of a number, we can multiply the number by \(\frac{135}{100}\) or 1.35.
To find 6% of a number, we can multiply the number by \(\frac{6}{100}\) or 0.06.

In general, to find \(P\%\) of \(x\), we can multiply: \(\displaystyle \frac{P}{100} \boldcdot x\)