Lesson 12
Percentages and Tape Diagrams
12.1: Notice and Wonder: Tape Diagrams (5 minutes)
Warm-up
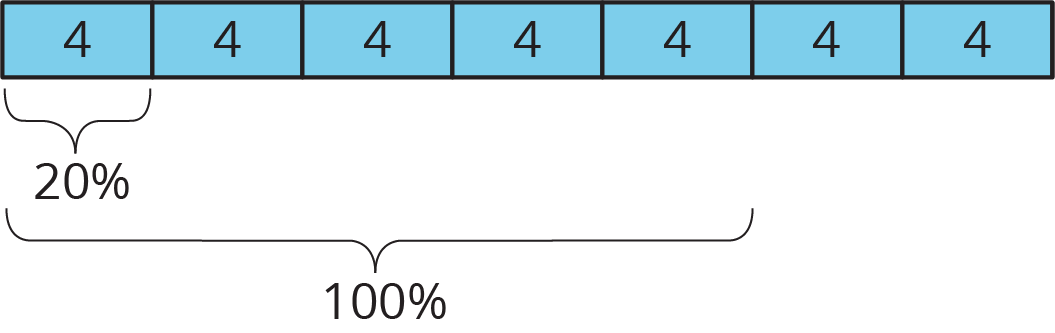
The purpose of this warm-up is to elicit the idea that tape diagrams can be used to think about fractions of a whole as percentages of the whole, which will be useful when students interpret and draw tape diagrams in a later activity. While students may notice and wonder many things about these images, the important discussion points are that there are two rectangles of the same length, one of the rectangles is divided into four pieces of equal length, and a percentage is indicated.
Launch
Arrange students in groups of 2. Tell students that they will look at an image, and their job is to think of at least one thing they notice and at least one thing they wonder. Display the image for all to see. Ask students to give a signal when they have noticed or wondered about something. Give students 1 minute of quiet think time and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. If possible, record the relevant reasoning on or near the image. After each response, ask the class if they agree or disagree and to explain alternative ways of thinking, referring back to the images each time. If the four pieces of equal length do not come up during the conversation, ask students to discuss this idea. It is not necessary to decide what should be used in place of the question mark.
12.2: Revisiting Jada's Puppy (15 minutes)
Activity
The purpose of this activity is for students to study and make sense of tape diagrams that can be used to see benchmark percentages in terms of fractions. The first question shows a percentage as a part of the whole, and the second shows a comparison between two quantities. Both situations can be described in terms of fractions or percentages. The second situation is important for making connections between percentages greater than 100 and fractions greater than 1.
Launch
Give students 1 minute of quiet think time, and then have them turn to a partner to discuss the first question. Poll the class to be sure that everyone can see that the puppy is \(\frac15\) of its adult weight. Ask the students what 100% is in this situation, and label the diagram with 100%. Give students 1 minute of quiet think time, and then have them discuss the second question with a partner.
Supports accessibility for: Organization; Attention
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Jada has a new puppy that weighs 9 pounds. It is now at about 20% of its adult weight.
-
Here is a diagram that Jada drew about the weight of her puppy.

-
The adult weight of the puppy will be 45 pounds. How can you see that in the diagram?
-
What fraction of its adult weight is the puppy now? How can you see that in the diagram?
-
-
Jada’s friend has a dog that weighs 90 pounds. Here is a diagram Jada drew that represents the weight of her friend’s dog and the weight of her puppy.

- How many times greater is the dog’s weight than the puppy’s?
- Compare the weight of the puppy and the dog using fractions.
- Compare the weight of the puppy and the dog using percentages.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Display the second diagram for all to see.


12.3: 5 Dollars (15 minutes)
Activity
The purpose of this activity is for students to describe multiplicative comparison problems given in terms of percentages using fractions.
Launch
Give students 3 minutes of quiet work time. Have them turn to a partner to discuss their answer to the first question. Then give them 3 minutes of quiet think time for the second question, followed by a whole-class discussion.
Supports accessibility for: Visual-spatial processing
Design Principle(s): Support sense-making
Student Facing
Noah has $5.
-
- Elena has 40% as much as Noah. How much does Elena have?
- Compare Elena’s and Noah’s money using fractions. Draw a diagram to illustrate.
-
- Diego has 150% as much as Noah. How much does Diego have?
-
Compare Diego’s and Noah’s money using fractions. Draw a diagram to illustrate.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Have students show and explain their diagrams. Then show these if no one has something equivalent:


12.4: Staying Hydrated (10 minutes)
Optional activity
In this activity, students explore percentages that describe parts of a whole. They find both \(B\) and \(C\), where \(A\%\) of \(B\) is \(C\), in the context of available and consumed water on a hike.
Students who use a double number line may notice that the value of \(B\) is the same in both questions, so the same double number line can be used to solve both parts of the problem. To solve the second question, however, the diagram needs to be partitioned with more tick marks.
As in the previous task, students may solve using other strategies, including by simply multiplying or dividing, i.e., \((1.5) \boldcdot 2 = 3.0\) and \(\frac{80}{100} \boldcdot (3.0) = 2.4\). Encourage them to also explain their reasoning with a double number line, table, or tape diagram. Monitor for at least one student using each of these representations.
Launch
Give students quiet think time to complete the activity and then time to share their explanation with a partner. Follow with a whole-class discussion.
Student Facing
During the first part of a hike, Andre drank 1.5 liters of the water he brought.
- If this is 50% of the water he brought, how much water did he bring?
- If he drank 80% of his water on his entire hike, how much did he drink?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Decide if each scenario is possible.
- Andre plans to bring his dog on his next hike, along with 150% as much water as he brought on this hike.
- Andre plans to drink 150% of the water he brought on his hike.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
After students create a double number line diagram with tick marks at 50% and 100%, some may struggle to know how to fit 80% in between. Encourage them to draw and label tick marks at 10% increments or work with a table instead. Some students may think that the second question is asking for the amount of water Andre drank on the second part of the hike. Clarify that it is asking for his total water consumption on the entire hike.
Activity Synthesis
Select 1–2 students who used a double number line, a table of equivalent ratios, and a tape diagram to share their strategies. As students explain, illustrate and display those representations for all to see.
Ask students how they knew what 100% means in the context. At this point it is not necessary for students to formally conceptualize the two ways percentages are used (to describe parts of whole, and to describe comparative relationships). Drawing their attention to concrete and contextualized examples of both, however, serves to build this understanding intuitively.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
If you are comparing two quantities using percentages, you can also compare them using fractions. Drawing a tape diagram can sometimes help us see how to do this more easily.
Questions for discussion:
- If you have 50% of the money needed to buy a book, what fraction is that?
- If you run 125% of your goal for the week, what fraction is that?
Seeing percentages in terms of fractions can help us solve percentage problems.
12.5: Cool-down - Small and Large (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Tape diagrams can help us make sense of percentages.
Consider two problems that we solved earlier using double number lines and tables: “What is 30% of 50 pounds?” and “What is 100% of a number if 140% of it is 28?”
Here is a tape diagram that shows that 30% of 50 pounds is 15 pounds.
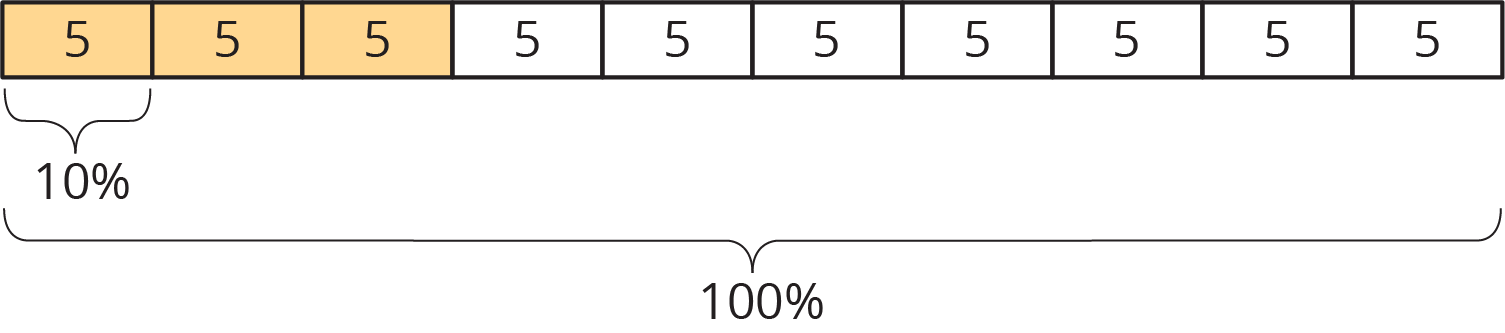
This diagram shows that if 140% of some number is 28, then that number must be 20.