Lesson 17
Painting a Room
17.1: Getting Ready to Paint (5 minutes)
Warm-up
This warm-up prompts students to start thinking about painting a room, the central context of this culminating lesson. Since not all students would have had experience painting a room or seeing one painted, an introduction helps make sure that the context is understood.
Students brainstorm a list of necessary tools and consider what it might take to paint a room, including building an initial idea of associated costs.
Launch
Tell students that their next project is about painting a room and their first task is to think about necessary supplies. Poll the class to find out who has experience painting a room. If possible, arrange students into small groups such that each group has at least one experienced person to help with the brainstorming. If no students (or only one or two) are familiar with room painting, consider finding and showing a video of someone doing detail painting. Ask students to notice the tools used in the work.
Student Facing
What are some tools that are helpful when painting a room?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students had a chance to brainstorm, invite groups to share their lists of necessary tools. Record and display the list for all to see and to refer to throughout the lesson. If possible, add the estimated cost of each item with the exception of the cost of the paint, since that will depend on the amount needed to paint the room. Alternatively, after the list is made, let students know that many hardware stores sell “painting kits” that include brushes, rollers, a tray, and a plastic drop sheet for around $20.
17.2: How Much It Costs to Paint (35 minutes)
Activity
This activity is comprised of two major parts: finding the total wall area to be painted and estimating needed supplies and associated costs. Students use a floor plan of a bedroom and a list of its features and measurements to calculate the room’s total wall area. They then use the square footage to make purchasing decisions and estimate costs.
Because of the variations in the bedroom’s walls and features, keeping track of the shapes to be included or excluded from the area calculation may be challenging to students. Look out for likely omissions or missed steps. For examples, students may neglect to:
- Include the 3 square feet of wall space above the door.
- Account for the south face of the small wall at one end of the closet. (At 0.5 feet wide and 8 feet tall, it accounts for 4 square feet of paintable surface area.)
- Account for the area above or below the window.
- Convert lengths to a common unit before determining area or before adding areas of different faces of the room. As students work, notice those who organize their work methodically and those who may need organizational support.
Launch
Since students may not be familiar with floor plans, consider spending a few minutes making sense of one as a class before working on the task. Display a floor plan of the classroom and identify where and how different features of the classroom (doors, windows, closets, etc.) are represented on the the plan.
Give students 2–3 minutes to read the task statement individually and to note any questions that come to mind. Afterwards, ask a couple of students to restate the task in their own words, and spend a few minutes answering any clarifying questions students may have.
Arrange students in groups of 2. Give students approximately 15 minutes of quiet think time to complete the first question (determining the total wall area to be painted). Ask students to discuss their work with their partner afterwards, and to pause for a whole-class debrief before moving on to the rest of the task.
Select a few students to share their strategies and solutions for the total wall area. Discuss any disagreements or questions in the shared calculation or approach. Make sure that the class agrees on the total square feet before instructing students to complete the rest of the task individually.
Supports accessibility for: Organization; Attention
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
Here is the floor plan for a bedroom:
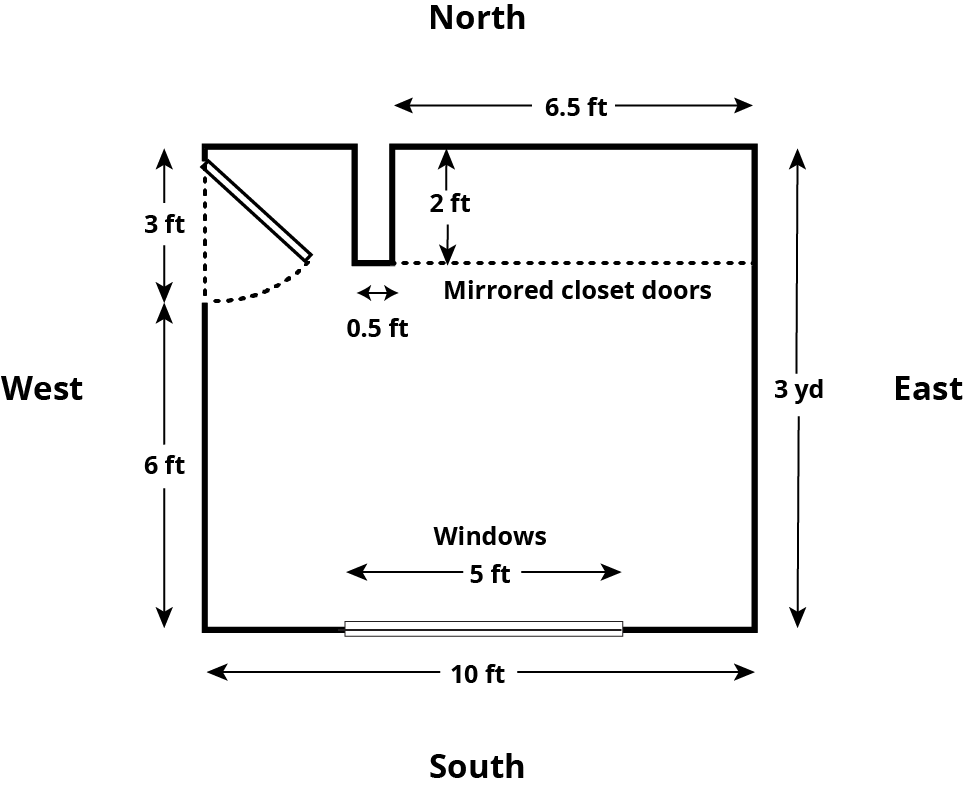
Imagine you are planning to repaint all the walls in this room, including inside the closet.
-
The east wall is 3 yards long.
-
The south wall is 10 feet long but has a window, 5 feet by 3 feet, that does not need to be painted.
-
The west wall is 3 yards long but has a door, 7 feet tall and 3 feet wide, that does not need to be painted.
-
The north wall includes a closet, 6.5 feet wide, with floor-to-ceiling mirrored doors that do not need to be painted. There is, however, a smaller wall between the west wall and the closet that does need to be painted on all sides. The wall is 0.5 feet wide and extends 2 feet into the room.
-
The ceiling in this room is 8 feet high.
-
All of the corners are right angles.
- If you paint all the walls in the room, how many square feet do you need to cover?
-
An advertisement about the paint that you want to use reads: “Just 2 quarts covers 175 square feet!” If you need to apply two coats of paint on all the walls, how much paint do you need to buy?
- Paint can only be purchased in 1-quart, 1-gallon, and 5-gallon containers. How much will all supplies for the project cost if the cans of paint cost $10.90 for a quart, $34.90 for a gallon, and $165.00 for 5 gallons?
- You have a coupon for 20% off all quart-sized paint cans. How does that affect the cost of the project?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Begin by asking 1–2 students to explain their calculations on how much paint is needed. Students should see that using the total wall area alone to find the volume of paint to purchase is not going to be adequate, since two full coats are needed, and paint can only be purchased in specific quantities. How students account for these factors in their decisions and calculations may vary. For example, some students may prefer buying fewer containers of a larger quantity while others may prefer buying more containers of a smaller quantity. Some may choose to have as little extra paint as possible, while other may choose otherwise. (To have enough paint, students may choose to purchase 7 quart-sized containers, 2 gallon-sized containers, or 3 quart-sized and 1 gallon-sized containers.)
Once students have a chance to discuss the various ways students chose to purchase paint, discuss their cost estimates. Consider setting up a few ranges of costs (e.g., $80–$84.99, $85–$89.99, $90–$94.99, $95–$99.99, $100 or more, etc.) and polling students on where their cost estimates land. Their estimates vary depending on the containers chosen, supplies included, and other assumptions or decisions they made.
Ask, “Can all of these values be correct?” Give students a moment of quiet think time before selecting 2–3 to respond and to share how they calculated their estimates. Record and display students’ responses to help everyone make sense of how the different costs are possible. For example, students who decided that a minimum of 7 total quarts of paint are needed may have reasoned as follows: Cost of painting supplies + cost for 1 gallon container + cost of 3 quart containers = total cost. $ For the final question of the activity, select a student with a successful strategy to share how they applied the coupon. Consider wrapping up the activity by asking how to purchase the paint and use the coupon to get the best deal.
17.3: How Long It Takes to Paint (15 minutes)
Activity
In this activity, students use the area measures from the previous task to solve problems about the amount of painting time, using their understanding of ratio, rate, and percentage along the way. The problems can be approached in a number of ways, giving students additional opportunities to model with mathematics (MP4) and choose their tools (MP5).
Launch
Give students quiet think time to complete the activity and then time to share their work and solutions with a partner. Ask students to be ready to explain their partner’s strategy to the class (MP3).
Student Facing
After buying the supplies, you start painting the east wall. It takes you 96 minutes to put two coats of paint on that wall (not including a lunch break between the two coats).
-
Your friend stops by to see how you are doing and comments that you are 25% finished with the painting. Are they correct?
- Your friend offers to help you with the rest of the painting. It takes the two of you 150 more minutes of painting time to finish the entire room. How much time did your friend save you?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may try to account for the amount of time that it takes the paint to dry between applying the first and second coat. Point out the the problem is only referring to the painting time, not the drying time.
Activity Synthesis
After students have conferred with their partners and checked their solutions (which for this activity is important, since a correct answer to the first problem is needed to find a correct answer to the second problem), debrief as a class. Invite students who thought their partner used a particularly efficient strategy to share.
In the first problem, students may solve it by figuring out that 3 square feet is 1% and scaling it to 72 square feet to correspond to 24%. If this was the dominant strategy in the class, make sure to emphasize how students can solve this problem by calculating \(\frac{72}{300} \boldcdot 100\) directly.