Lesson 11
Percentages and Double Number Lines
11.1: Fundraising Goal (5 minutes)
Warm-up
This warm-up is the first time students are asked to find \(A\%\) of \(B\) when \(B\) is not 100 or 1.
Students may approach the problem in a few different ways, with or without filling in values on the provided double number line diagram. For example, they may understand from the fundraising context of the problem that \$40 is 100% because it is the amount of the goal. From there, they may simply find half of \$40 for the 50% value and add that value to \$40 to find the 150% value. Other students may use equivalent ratio reasoning to calculate the value at 50% and 150%. As students work, notice the different strategies used and any misconceptions so they can be addressed during discussion.
Launch
Remind students that in the previous lesson, we found percentages of 100 and of 1 using double number lines. Explain that in this lesson we will find percentages of other numbers. Give students 2 minutes of quiet work time, and follow with a whole-class discussion. Encourage students to create a double number line to help them answer the questions if needed.
Student Facing
Each of three friends—Lin, Jada, and Andre—had the goal of raising $40. How much money did each person raise? Be prepared to explain your reasoning.
-
Lin raised 100% of her goal.
-
Jada raised 50% of her goal.
-
Andre raised 150% of his goal.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may be surprised by a percentage greater than 100. If they are puzzled by this, explain that Andre raised more money than the goal.
Activity Synthesis
Consider displaying this double number line for all to see.

Invite a few students to share their solving strategies. One way to highlight the different techniques students use is to invite several students to explain how they calculated the amount of money raised by Andre. We can find 150% of 40 in several ways. For example, we can add the values of 50% of 40 and 100% of 40. We can also reason that since \(100 \boldcdot (1.5) = 150\) then \(40 \boldcdot (1.5) = 60\), which means \$60 is 150% of \$40.
If not uncovered in students’ explanations, explain that we are finding percentages of \$40, since this number—not 100 cents or 1 dollar—is the fundraising goal for the three friends. Since 100% of a goal of \$40 is \$40, the 100% and \$40 are lined up on the double number line.
Students who relied on the visual similarity between, for example, \$0.25 is 25% of 1 dollar in the previous lesson find this strategy unworkable here (as \$50 is not 50% of \$40). To encourage students to use their understanding of equivalent ratios to reason about percent problems, ask the class to explain—either when the above misconception arises or as a closing question—why \$50 is not 50% of \$40, but 50% of 100 cents is 50 cents.
11.2: Three-Day Biking Trip (15 minutes)
Activity
In this activity, students find percentages of a value in a non-monetary context. They begin by assigning a value to 100% and reasoning about other percentages.
The double number line is provided to communicate that we can use all our skills for reasoning about equivalent ratios to reason about percentages. Providing this representation makes it more likely that students will use it, but it would be perfectly acceptable for them to use other strategies.
Monitor for students using these strategies:
- Use a double number line and reason that since 25% is \(\frac14\) of 100%, 25% of 8 is \(8\boldcdot \frac14 = 2\). They may then skip count by the value for the first tick mark to find the values for other tick marks.
- Reason about 125% of the distance as 100% of the distance plus 25% of the distance, and add 8 and \(\frac14\) of 8.
- Reason about 75% of 8 directly by multiplying 8 by \(\frac34\) and 125% of 8 by multiply 8 by \(\frac54\).
Launch
Arrange students in groups of 3–4. Provide tools for making a large visual display. Give students 2–3 minutes of quiet think time. Encourage students to use the double number line to help them answer the questions if needed. Afterwards, ask them to discuss their responses to the last two questions with their group and to create a visual display of one chosen strategy to be shared with the class.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Elena biked 8 miles on Saturday. Use the double number line to answer the questions. Be prepared to explain your reasoning.

-
What is 100% of her Saturday distance?
-
On Sunday, she biked 75% of her Saturday distance. How far was that?
-
On Monday, she biked 125% of her Saturday distance. How far was that?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
For each unique strategy, select one group to share their displays and explain their thinking. Sequence the presentations in the order they are presented in the Activity Narrative. If no students mention one or more of these strategies, bring them up. For example, if no one thought of 125% of the distance hiked as 100% plus 25%, present that approach and ask students to explain why it works.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
11.3: Puppies Grow Up (15 minutes)
Activity
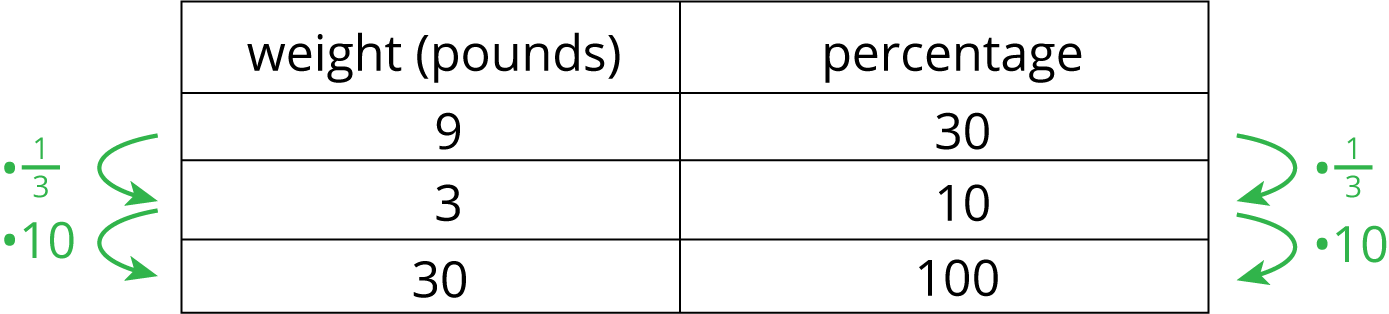
Previously students were asked to find various percentages given 100% of a quantity. Here they are asked to find 100% of quantities given other percentages. The context does not explicitly state that the values being sought (the adult weights of two puppies) are the values for 100%, so students will first need to make that connection.
Double number lines continue to be provided as a reasoning tool, but students may use a table of equivalent ratios or other methods. Those who use double number lines are likely to find them effective for the first question (find 100% of a quantity given 20%) but less straightforward for the second question (find 100% of a quantity given 30%). Since 100 is not a multiple of 30, students may use strategies such as subdividing the double number line into intervals of 10% and scaling up from there to find the value of 100%.
Launch
Arrange students in groups of 2. Give students 3–4 minutes of quiet think time and then time to share their responses with their partner. Encourage students to refer to diagrams in previous activities if they are not sure how to get started. Students may need help interpreting the question to understand that 100% corresponds to the puppy’s adult weight.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
-
Jada has a new puppy that weighs 9 pounds. The vet says that the puppy is now at about 20% of its adult weight. What will be the adult weight of the puppy?

-
Andre also has a puppy that weighs 9 pounds. The vet says that this puppy is now at about 30% of its adult weight. What will be the adult weight of Andre’s puppy?

- What is the same about Jada and Andre’s puppies? What is different?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A loaf of bread costs $2.50 today. The same size loaf cost 20 cents in 1955.
- What percentage of today’s price did someone in 1955 pay for bread?
- A job pays $10.00 an hour today. If the same percentage applies to income as well, how much would that job have paid in 1955?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may stop before they reach 100% or go further than 100%. If this happens, explain that in this situation, the adult weight is at exactly 100%. Students may not use equal-sized increments between the tick marks they draw and label.
Activity Synthesis
Invite previously identified students to share their work. Start with someone who solved the first question using a double number line as follows, and follow with increasingly efficient strategies. Keep the number line displayed for all to see and to refer to throughout discussion.

If no students reasoned with a table, display this abbreviated table, or illustrate one student’s approach and organize the steps in a table.

Follow a similar flow when discussing strategies for solving the second problem: start with a double number line and, if not mentioned by students, discuss how a table such as this one can be an efficient tool.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Lesson Synthesis
Lesson Synthesis
If you know the percentage and 100%, then you can find the percentage with a double number line by putting the value assigned to 100% opposite the tick mark labeled 100%. For example, if we want to find some percentage of 50 pounds, we can label 100% and 50 like this:

Display the table for all to see. Questions for discussion:
- What situation might this double number line represent?
- This says that 100% of 50 is 50. Where can we place some other percentages of 50?
- (If no one mentions a percentage greater than 100%) What about 110% of 50? Where would we place it? How would it be labeled?
11.4: Cool-down - A Medium Bottle of Juice (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
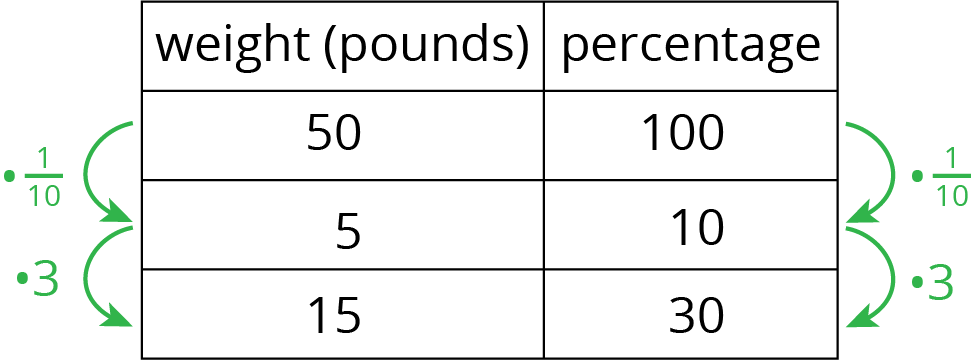
We can use a double number line to solve problems about percentages. For example, what is 30% of 50 pounds? We can draw a double number line like this:

We divide the distance between 0% and 100% and that between 0 and 50 pounds into ten equal parts. We label the tick marks on the top line by counting by 5s (\(50 \div 10 = 5\)) and on the bottom line counting by 10% (\(100 \div 10 =10\)). We can then see that 30% of 50 pounds is 15 pounds.
We can also use a table to solve this problem.
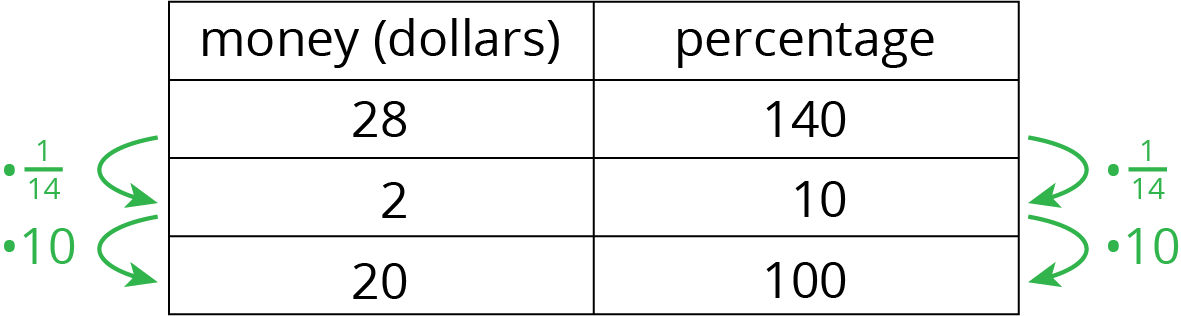
Suppose we know that 140% of an amount is \$28. What is 100% of that amount? Let’s use a double number line to find out.

We divide the distance between 0% and 140% and that between \$0 and \$28 into fourteen equal intervals. We label the tick marks on the top line by counting by 2s and on the bottom line counting by 10%. We would then see that 100% is \$20.
Or we can use a table as shown.