Lesson 13
Benchmark Percentages
13.1: What Percentage Is Shaded? (5 minutes)
Warm-up
In this warm-up, students are presented with tape diagrams with a shaded portion, and they identify the percentage that is shaded.
Launch
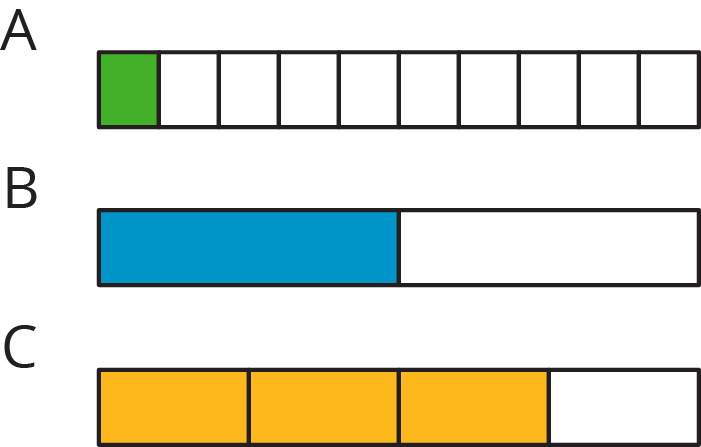
Display the image in the task statement for all to see, and ask students to think of at least one thing they notice. Ask a few students to share something they notice. It is likely that students notice there are three tape diagrams of the same length, but the first is divided into 10 equal pieces, the second into 2 equal pieces, and the last into 4 equal pieces. Students may make claims about what fraction of each tape is shaded. Remind students that when we wonder, "What percent of something is shaded?" it is understood that the whole thing is 100%.
Arrange students in groups of 2. Give 1–2 minutes of quiet think time, followed by partner- and whole-class discussions.
Student Facing
What percentage of each diagram is shaded?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share how they reasoned about the percentage of each tape diagram that is shaded. Record and display their explanations for all to see. Highlight alternative ways of naming the size of the shaded portion, for example, “\(\frac34\) of the diagram” and “75% of the diagram.”
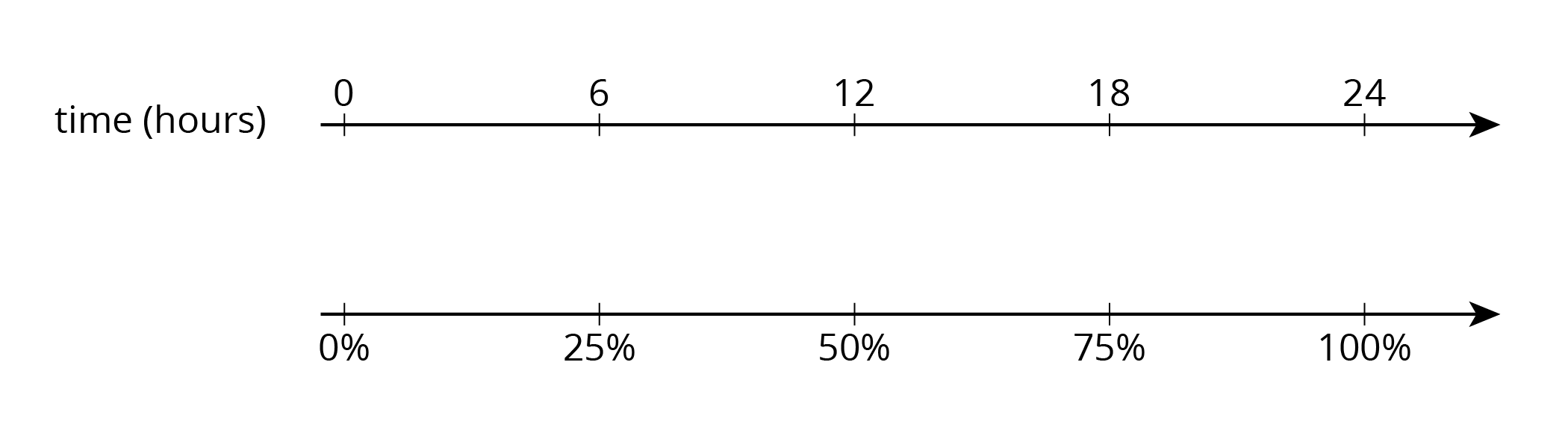
13.2: Liters, Meters, and Hours (15 minutes)
Activity
In this activity, students calculate three different benchmark percentages—50%, 10%, and 75%—given three different values that correspond to 100%. The repetition of the benchmark percentages allows students to notice regularity and engage in MP8. They generalize the patterns in their calculations to determine how to find those percentages when the 100% value is \(x\).
Launch
Ask students to complete the first three sub-questions of each problem mentally. If necessary, clarify that “using mental math” means working out an answer without writing down their calculations and just recording the answer. For the last sub-question, ask them to write a sentence or two to explain their approach. Give students quiet think time to complete the activity and then time to share their explanation with a partner.
Supports accessibility for: Memory; Organization
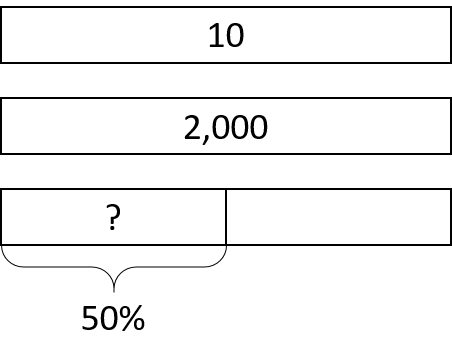
Student Facing
-
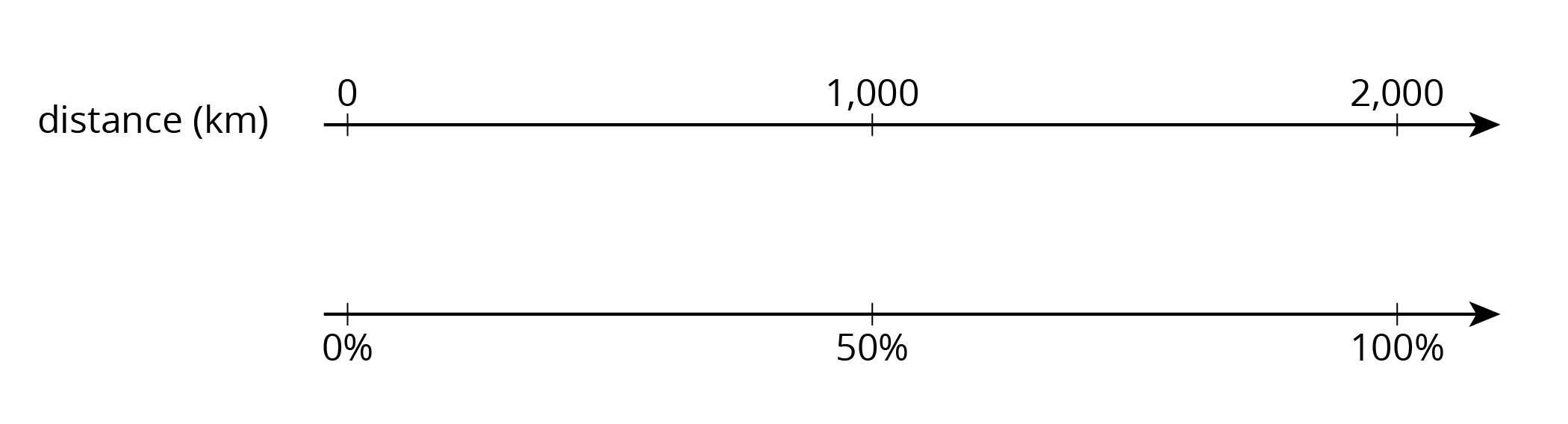
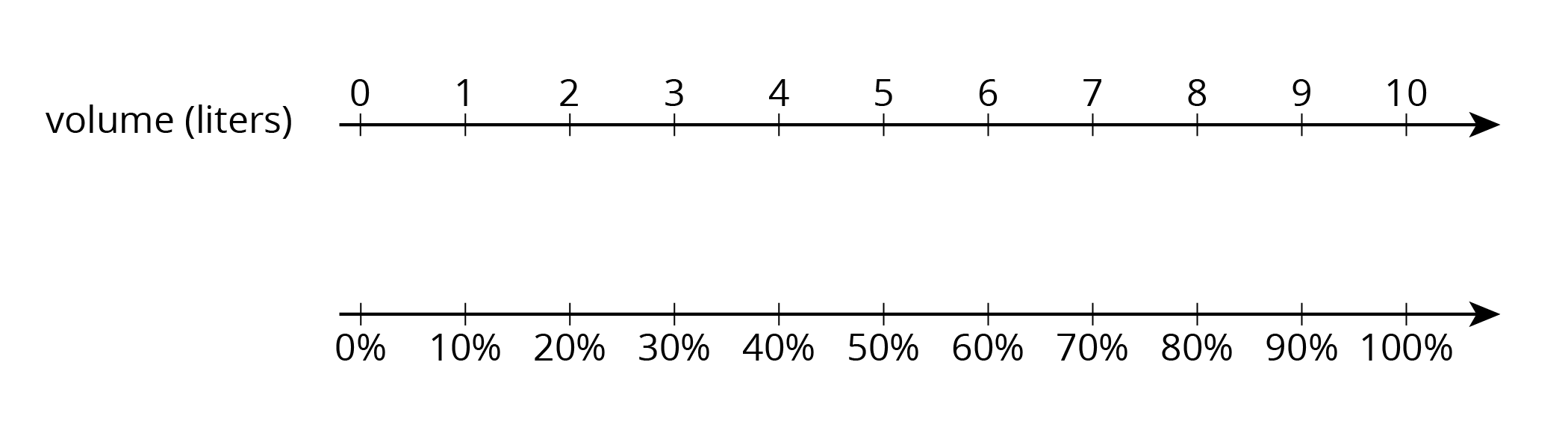
- How much is 50% of 10 liters of milk?
- How far is 50% of a 2,000-kilometer trip?
- How long is 50% of a 24-hour day?
- How can you find 50% of any number?
-
- How far is 10% of a 2,000-kilometer trip?
- How much is 10% of 10 liters of milk?
- How long is 10% of a 24-hour day?
- How can you find 10% of any number?
-
- How long is 75% of a 24-hour day?
- How far is 75% of a 2,000-kilometer trip?
- How much is 75% of 10 liters of milk?
- How can you find 75% of any number?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to get started with mental math, offer some scaffolding. For example, ask, “How much of 100% is 50%?” Suggest to students that if they know that 50% of a number is the same as \(\frac12\) of that number, then they can think about what \(\frac12\) of the number is.
Activity Synthesis
Highlight the following:
50% of a quantity is \(\frac12\) of that quantity. We can calculate it by dividing the quantity by 2 or multiplying the quantity by \(\frac12\). If no students bring up the multiplication method, ask what fraction 50% reminds them of or what number they could multiply by to get the same answer; either \(\frac12\) or 0.5 is fine.
10% of a quantity is \(\frac{1}{10}\) of that quantity. You can calculate it by dividing the quantity by 10, or multiplying the quantity by \(\frac{1}{10}\).
75% of a quantity is \(\frac34\) of that quantity. You can calculate it by dividing the quantity by four and then multiplying by 3, or by multiplying the quantity by \(\frac34\).
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
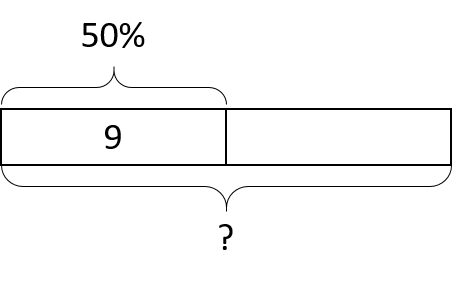
13.3: Nine is . . . (10 minutes)
Activity
In this activity students find the values for 100% given different benchmark percentages. Students are likely to calculate the answers quickly. They are to spend the majority of the task time discussing how they reason about the questions.
Launch
Give students quiet think time to complete the activity and then time to share their explanations with a partner.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Explain how you can calculate each value mentally.
- 9 is 50% of what number?
- 9 is 25% of what number?
- 9 is 10% of what number?
- 9 is 75% of what number?
- 9 is 150% of what number?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think 9 is 100% and try to find the percentage of the number given. You can use the diagram in the task statement to help them make sense of the first question and then encourage them to use mental math, or draw additional diagrams, to solve the other four questions.
Activity Synthesis
Invite students to share different strategies for answering the questions, with or without using fractions. For example, some may multiply the given 9 by 2, 4, and 10, respectively, to find values of 100% given the values of 50%, 25%, and 10% in the first three problems. Highlight any fractions students used to make sense of and solve the problems.
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
13.4: Matching the Percentage (10 minutes)
Optional activity
In this activity, students calculate benchmark percentages. Students are likely to calculate the answers quickly They are to spend the majority of the task time discussing how they reason about the questions.
Launch
Give students quiet think time to complete the activity and then time to share their explanation with a partner.
Supports accessibility for: Language; Conceptual processing
Student Facing
Match the percentage that describes the relationship between each pair of numbers. One percentage will be left over. Be prepared to explain your reasoning.
-
7 is what percentage of 14?
-
5 is what percentage of 20?
-
3 is what percentage of 30?
-
6 is what percentage of 8?
-
20 is what percentage of 5?
- 4%
- 10%
- 25%
- 50%
- 75%
- 400%
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- What percentage of the world’s current population is under the age of 14?
- How many people is that?
- How many people are 14 or older?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Because 5 goes into 20 four times, students may answer that 5 is 4% of 20. If this happens, explain that 5 is really \(\frac14\) of 20 and ask them what percentage represents one quarter.
Activity Synthesis
Invite students to share their mental math strategies. If needed, consider illustrating the relationship between of \(B\) and \(C\) (where \(A\%\) of \(B\) is \(C\)) using tape diagrams or double number line diagrams to help students visualize the association between the benchmark percentages and fractions.
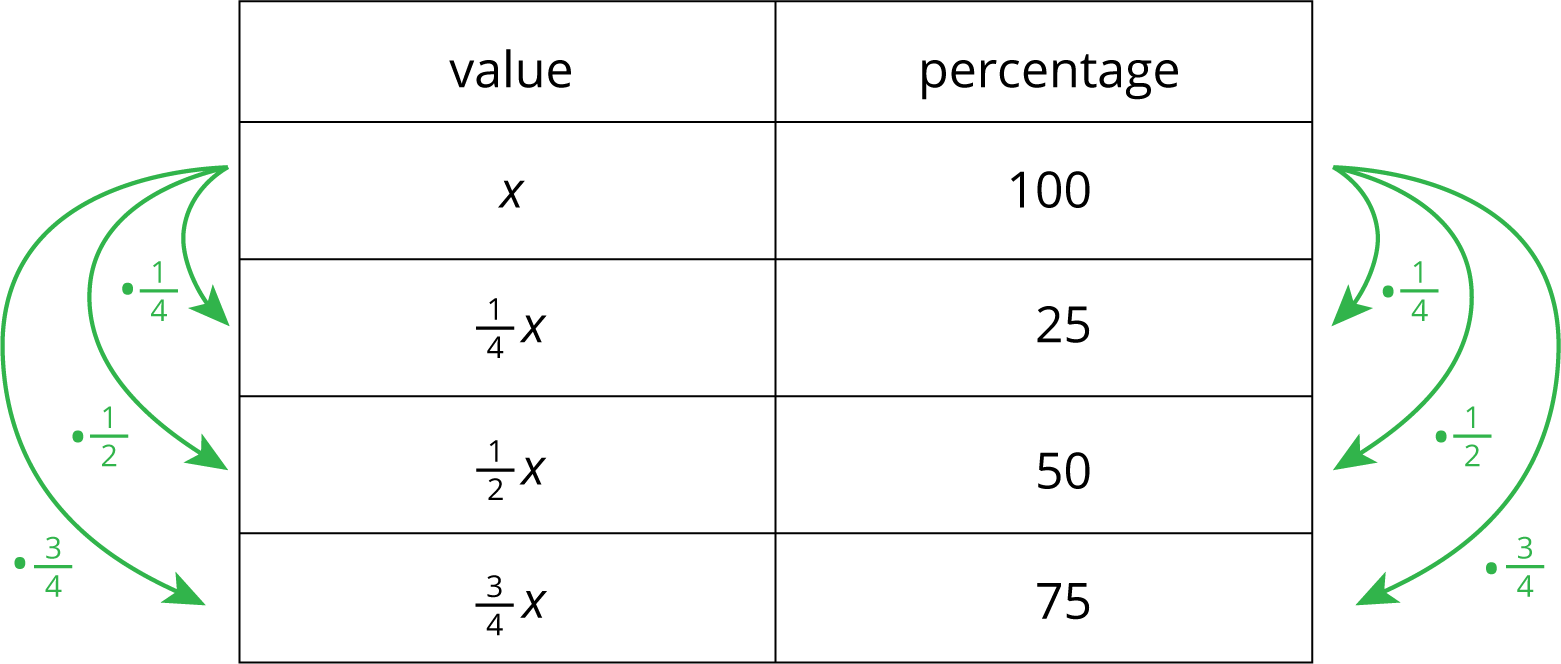
Lesson Synthesis
Lesson Synthesis
Certain percentages are easy to think about in terms of fractions. Ask students how they can think about each benchmark percentage by using a fraction. Demonstrate the correspondences using a double number line, tape diagram, or a table (as shown).
- 25% of a number is always \(\frac14\) of that number.
- 50% of a number is always \(\frac12\) of that number.
- 75% of a number is always \(\frac34\) of that number
- 10% of a number is always \(\frac{1}{10}\) of that number.
13.5: Cool-down - Around the Clock (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Certain percentages are easy to think about in terms of fractions.
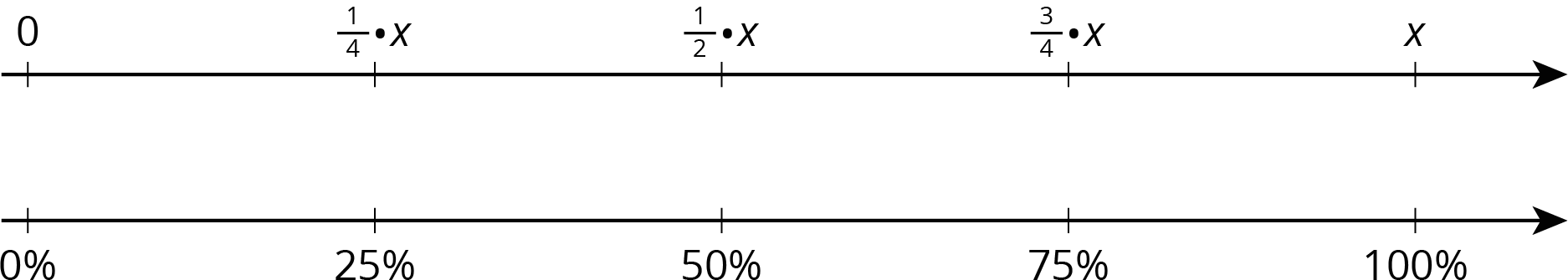
- 25% of a number is always \(\frac14\) of that number.
For example, 25% of 40 liters is \(\frac14 \boldcdot 40\) or 10 liters. - 50% of a number is always \(\frac12\) of that number.
For example, 50% of 82 kilometers \(\frac12 \boldcdot 82\) or 41 kilometers. - 75% of a number is always \(\frac34\) of that number.
For example, 75% of 1 pound is \(\frac34\) pound. - 10% of a number is always \(\frac{1}{10}\) of that number.
For example, 10% of 95 meters is 9.5 meters. - We can also find multiples of 10% using tenths.
For example, 70% of a number is always \(\frac{7}{10}\) of that number, so 70% of 30 days is \(\frac{7}{10} \boldcdot 30\) or 21 days.
