Lesson 12
How Much Will Fit?
Problem 1
- Sketch a cube and label its side length as 4 cm (this will be Cube A).
- Sketch a cube with sides that are twice as long as Cube A and label its side length (this will be Cube B).
- Find the volumes of Cube A and Cube B.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Two paper drink cups are shaped like cones. The small cone can hold 6 oz of water. The large cone is \(\frac43\) the height and \(\frac43\) the diameter of the small cone. Which of these could be the amount of water the large cone holds?
8 cm
14 oz
4.5 oz
14 cm
Solution
For access, consult one of our IM Certified Partners.
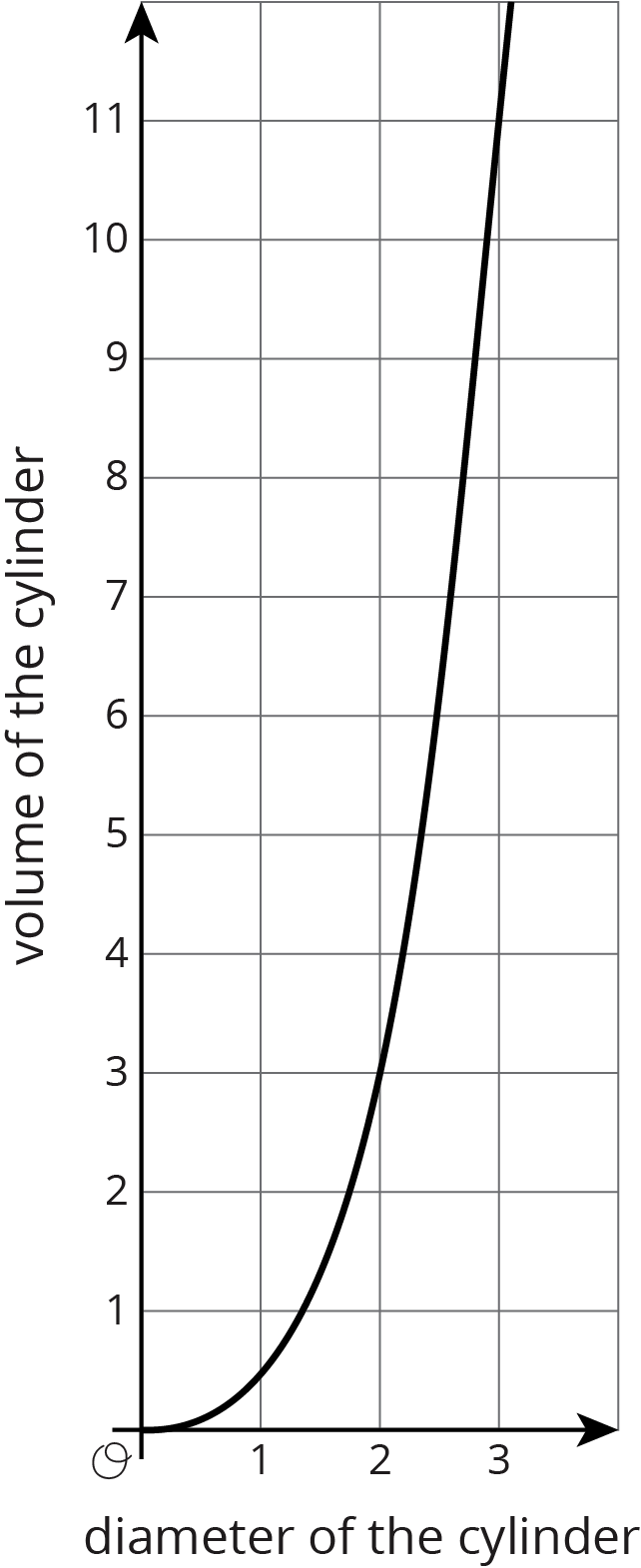
Problem 3
The graph represents the volume of a cylinder with a height equal to its radius.
- When the diameter is 2 cm, what is the radius of the cylinder?
- Express the volume of a cube of side length \(s\) as an equation.
- Make a table for volume of the cube at \(s = \) 0 cm, \(s = \) 1 cm, \(s = \) 2 cm, and \(s = \) 3 cm.
- Which volume is greater: the volume of the cube when \(s =\) 3 cm, or the volume of the cylinder when its diameter is 3 cm?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 5, Lesson 7.)Problem 4
Select all the points that are on a line with slope 2 that also contains the point \((2, \text-1)\).
\((3,1)\)
\((1,1)\)
\((1,\text-3)\)
\((4,0)\)
\((6,7)\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 10.)Problem 5
Several glass aquariums of various sizes are for sale at a pet shop. They are all shaped like rectangular prisms. A 15-gallon tank is 24 inches long, 12 inches wide, and 12 inches tall. Match the dimensions of the other tanks with the volume of water they can each hold.
Solution
For access, consult one of our IM Certified Partners.
Problem 6
Solve: \(\begin{cases} y=\text-2x-20 \\ y=x+4 \\ \end{cases}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 14.)