Lesson 12
How Much Will Fit?
Let’s reason about the volume of different shapes.
12.1: Two Containers
Your teacher will show you some containers. The small container holds 200 beans. Estimate how many beans the large jar holds.
12.2: What’s Your Estimate?
Your teacher will show you some containers.
- If the pasta box holds 8 cups of rice, how much rice would you need for the other rectangular prisms?
- If the pumpkin can holds 15 fluid ounces of rice, how much do the other cylinders hold?
- If the small cone holds 2 fluid ounces of rice, how much does the large cone hold?
- If the golf ball were hollow, it would hold about 0.2 cups of water. If the baseball were hollow, how much would the sphere hold?
12.3: Do You Know These Figures?
- What shapes are the faces of each type of object shown here? For example, all six faces of a cube are squares.

- Which faces could be referred to as a “base” of the object?
- Here is a method for quickly sketching a cylinder:
- Draw two ovals.
- Connect the edges.
- Which parts of your drawing would
be hidden behind the cylinder?
Make these parts dashed lines.
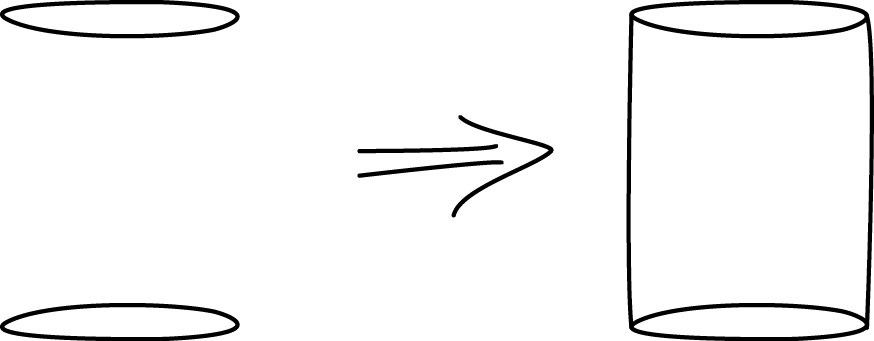
- Practice sketching some cylinders. Sketch a few different sizes, including short, tall, narrow, wide, and sideways. Label the radius \(r\) and height \(h\) on each cylinder.

A soccer ball is a polyhedron with 12 black pentagonal faces and 20 white hexagonal faces. How many edges in total are on this polyhedron?
Summary
The volume of a three-dimensional figure, like a jar or a room, is the amount of space the shape encloses. We can measure volume by finding the number of equal-sized volume units that fill the figure without gaps or overlaps. For example, we might say that a room has a volume of 1,000 cubic feet, or that a pitcher can carry 5 gallons of water. We could even measure volume of a jar by the number of beans it could hold, though a bean count is not really a measure of the volume in the same way that a cubic centimeter is because there is space between the beans. (The number of beans that fit in the jar do depend on the volume of the jar, so it is an okay estimate when judging the relative sizes of containers.)
In earlier grades, we studied three-dimensional figures with flat faces that are polygons. We learned how to calculate the volumes of rectangular prisms. Now we will study three-dimensional figures with circular faces and curved surfaces: cones, cylinders, and spheres.
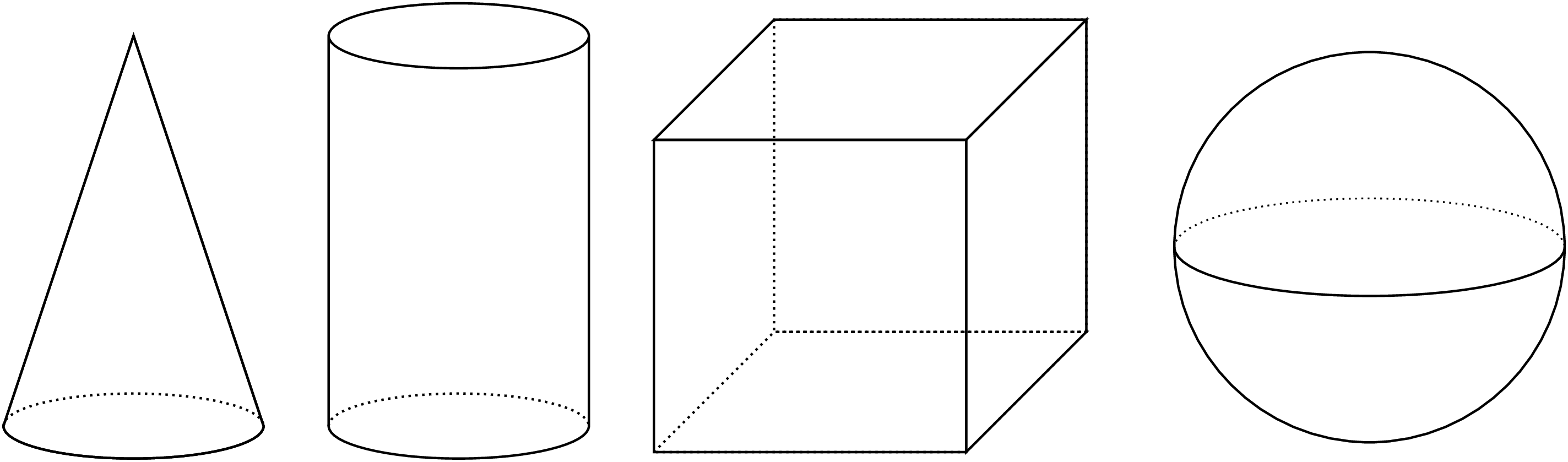
To help us see the shapes better, we can use dotted lines to represent parts that we wouldn't be able to see if a solid physical object were in front of us. For example, if we think of the cylinder in this picture as representing a tin can, the dotted arc in the bottom half of that cylinder represents the back half of the circular base of the can. What objects could the other figures in the picture represent?
Glossary Entries
- cone
A cone is a three-dimensional figure like a pyramid, but the base is a circle.
- cylinder
A cylinder is a three-dimensional figure like a prism, but with bases that are circles.
- sphere
A sphere is a three-dimensional figure in which all cross-sections in every direction are circles.