Lesson 3
Equations for Functions
3.1: A Square’s Area (5 minutes)
Warm-up
The purpose of this warm-up is for students to use repeated reasoning to write an algebraic expression to represent a rule of a function (MP8). The whole-class discussion should focus on the algebraic expression in the final row, however the numbers in the table give students an opportunity to also practice calculating the square of numbers written in fraction and decimal form.
Launch
Arrange students in groups of 2. Give students 1–2 minutes of quiet work time and then time to share their algebraic expression with their partner. Follow with a whole-class discussion.
Student Facing
Fill in the table of input-output pairs for the given rule. Write an algebraic expression for the rule in the box in the diagram.

| input | output |
|---|---|
| 8 | |
| 2.2 | |
| \(12\frac14\) | |
| \(s\) |
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share how they found each of the outputs. After each response, ask the class if they agree or disagree. Record and display responses for all to see. If both responses are not mentioned by students for the last row, tell students that we can either put \(s^2\) or \(A\) there. Tell students we can write the equation \(A = s^2\) to represent the rule of this function.
End the discussion by telling students that while we’ve used the terms input and output so far to talk about specific values, when a letter is used to represent any possible input we call it the independent variable and the letter used to represent all the possible outputs is the dependent variable. Students may recall these terms from earlier grades. In this case, \(s\) is the independent variable and \(A\) the dependent variable, and we say “\(A\) depends on \(s\).”
3.2: Diagrams, Equations, and Descriptions (15 minutes)
Activity
The purpose of this activity is for students to make connections between different representations of functions and start transitioning from input-output diagrams to other representations of functions. Students match input-output diagrams to descriptions and come up with equations for each of those matches. Students then calculate an output given a specific input and determine the independent and dependent variables.
Launch
Arrange students in groups of 2. Give students 3–5 minutes of quiet work time and time to share their responses with their partner and come to agreement on their answers. Follow with whole-class discussion.
Student Facing
Record your answers to these questions in the table provided.
- Match each of these descriptions with a diagram:
- the circumference, \(C\), of a circle with radius, \(r\)
- the distance in miles, \(d\), that you would travel in \(t\) hours if you drive at 60 miles per hour
- the output when you triple the input and subtract 4
- the volume of a cube, \(v\) given its edge length, \(s\)
- Write an equation for each description that expresses the output as a function of the input.
- Find the output when the input is 5 for each equation.
- Name the independent and dependent variables of each equation.
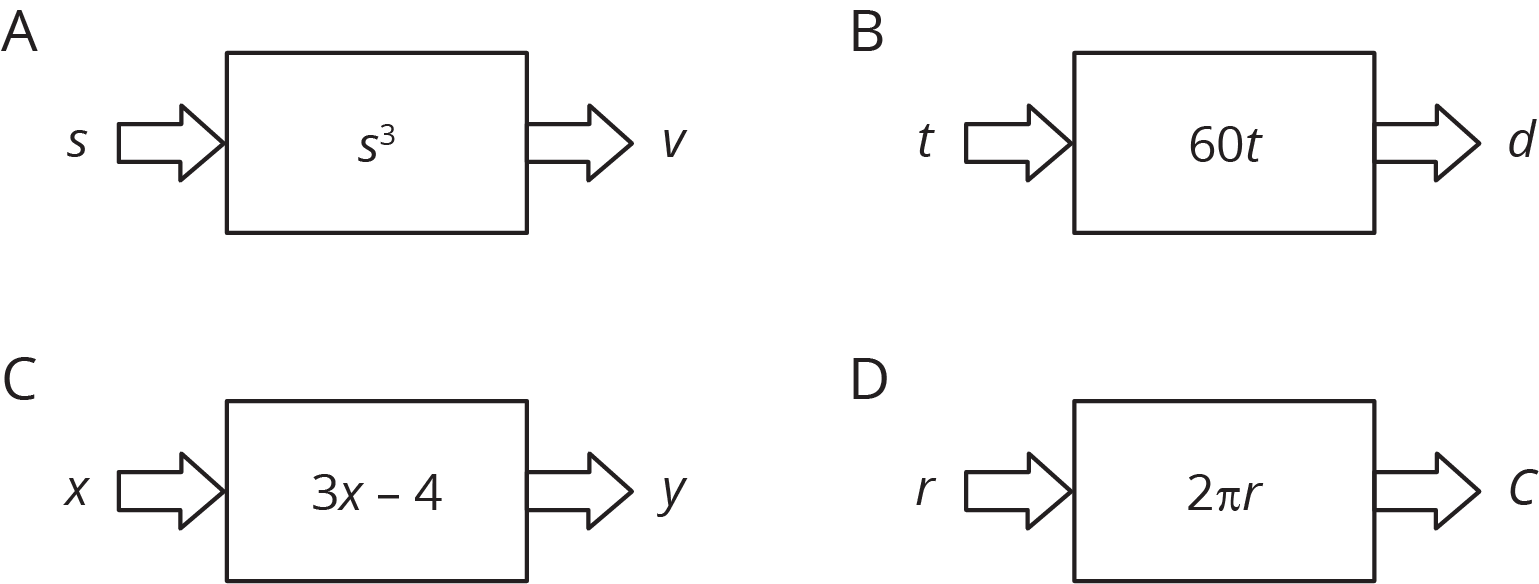
| description | a | b | c | d |
|---|---|---|---|---|
| diagram | ||||
| equation | ||||
| input = 5 output = ? |
||||
| independent variable |
||||
| dependent variable |
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Choose a 3-digit number as an input.
Apply the following rule to it, one step at a time:
- Multiply your number by 7.
- Add one to the result.
- Multiply the result by 11.
- Subtract 5 from the result.
- Multiply the result by 13
- Subtract 78 from the result to get the output.
Can you describe a simpler way to describe this rule? Why does this work?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is for students to describe the connections they see between the different entries for the 4 descriptions. Display the table for all to see and select different groups to share the answers for a column in the table. As groups share their answers, ask:
- “How did you know that this diagram matched with this description?” (We remembered the formula for the circumference of a circle, so we knew description A went with diagram D.)
- “Where in the equation do you see the rule that is in the diagram?” (The equation is the dependent variable set equal to the rule describing what happens to the independent variable in the diagram.)
- “Explain why you chose those quantities for your independent and dependent variables." (We know the independent variable is the input and the dependent variable is the output, so we matched them up with the input and output shown in the diagram.)
Design Principle(s): Support sense-making; Optimize output (for explanation)
3.3: Dimes and Quarters (15 minutes)
Activity
The purpose of this activity is for students to work with a function where either variable could be the independent variable. Knowing the total value for an unknown number of dimes and quarters, students are first asked to consider if the number of dimes could be a function of the number of quarters and then asked if the reverse is also true. Since this isn't always the case when students are working with functions, the discussion should touch on reasons for choosing one variable vs. the other, which can depend on the types of questions one wants to answer.
Identify students who efficiently rewrite the original equation in the third problem and the last problem to share during the discussion.
Launch
Arrange students in groups of 2. Give students 3–5 minutes of quiet work time followed by partner discussion for students to compare their answers and resolve any differences. Follow with a whole-class discussion.
Supports accessibility for: Language; Conceptual processing
Design Principle(s): Support sense-making
Student Facing
Jada had some dimes and quarters that had a total value of $12.50. The relationship between the number of dimes, \(d\), and the number of quarters, \(q\), can be expressed by the equation \(0.1d + 0.25q = 12.5\).
- If Jada has 4 quarters, how many dimes does she have?
- If Jada has 10 quarters, how many dimes does she have?
- Is the number of dimes a function of the number of quarters? If yes, write a rule (that starts with \(d = \)...) that you can use to determine the output, \(d\), from a given input, \(q\). If no, explain why not.
- If Jada has 25 dimes, how many quarters does she have?
- If Jada has 30 dimes, how many quarters does she have?
- Is the number of quarters a function of the number of dimes? If yes, write a rule (that starts with \(q=\)...) that you can use to determine the output, \(q\), from a given input, \(d\). If no, explain why not.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may be unsure how to write rules for the number of dimes as a function of the number of quarters and vice versa. Prompt them to use the provided equation and what they know about keeping equations equal to create the new equations.
Activity Synthesis
Select previously identified students to share their rules for dimes as a function of the number of quarters and quarters as a function of the number of dimes, including the steps they used to rewrite the original equation.
Tell students that if we write an equation like \(d = 125 - 2.5q\), this shows that \(d\) is a function of \(q\) because it is clear what the output (value for \(d\)) should be for a given input (value for \(q\)).
Display the diagrams for all to see:
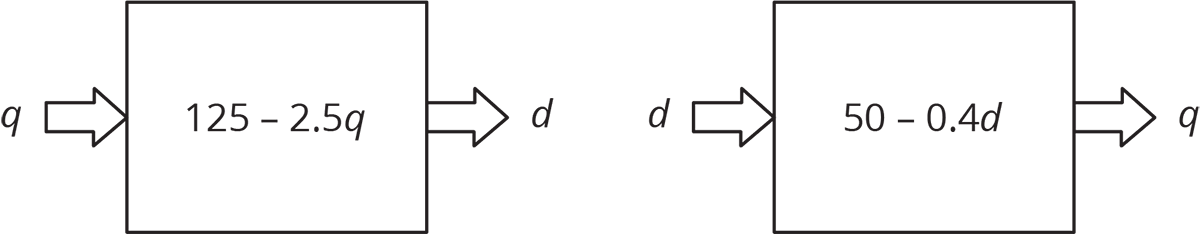
When we have an equation like \(0.1d + 0.25q = 12.5\), we can choose either \(d\) or \(q\) to be the independent variable. That means we are viewing one as depending on the other. If we know the number of quarters and want to answer a question about the number of dimes, it is helpful to write \(d\) as a function of \(q\). If we know the number of dimes and want to answer a question about the number of quarters, it is helpful to write \(q\) as a function of \(d\).
Ensure students understand that we can’t always do this type of rearranging with equations and have it make sense because sometimes only one variable is a function of the other, and sometimes neither is a function of the other. For example, students saw earlier that while squaring values is a function, the reverse—that is, identifying what value was squared—is not. We will continue to explore when these different things happen in future lessons.
Lesson Synthesis
Lesson Synthesis
Tell students that we often use independent and dependent variables to represent the inputs and outputs of functions. For some functions, we can describe the relationship between the variables with an equation. Sometimes we can choose, depending on the situation, which variable should be the independent and which should be the dependent variable. To help students think more about about what independent and dependent variables represent and their use with functions, ask:
- “How can we describe the area of square \(A\) of side length \(s\) with an equation? Which is the independent and which is the dependent variable?” (We can write \(s^2=A\), where \(s\) is the independent variable and \(A\) is the dependent variable.)
- “The relationship between the number of dimes, \(d\), and the number of nickels, \(n\), that total \$5 can be expressed by the equation \(0.1d+0.05n = 5\). When would it be useful to choose the number of dimes as the independent variable and rewrite the equation?” (If we knew the number of dimes and wanted to know the number of nickels, it would be useful to rewrite the equation so it looked like \(n= . . .\))
3.4: Cool-down - The Value of Some Quarters (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can sometimes represent functions with equations. For example, the area, \(A\), of a circle is a function of the radius, \(r\), and we can express this with an equation: \(\displaystyle A=\pi r^2\)
We can also draw a diagram to represent this function:
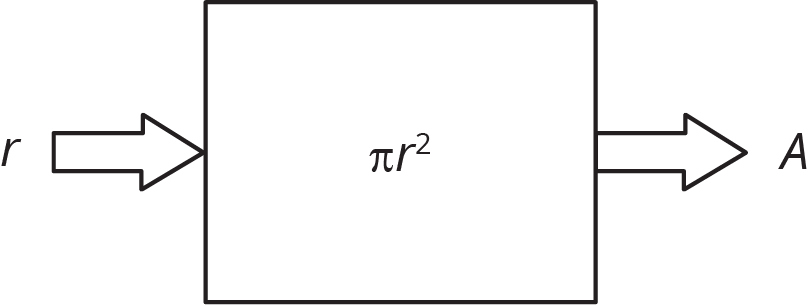
In this case, we think of the radius, \(r\), as the input, and the area of the circle, \(A\), as the output. For example, if the input is a radius of 10 cm, then the output is an area of \(100\pi\) cm2, or about 314 square cm. Because this is a function, we can find the area, \(A\), for any given radius, \(r\).
Since it is the input, we say that \(r\) is the independent variable and, as the output, \(A\) is the dependent variable.
Sometimes when we have an equation we get to choose which variable is the independent variable. For example, if we know that
\(\displaystyle 10A-4B=120\)
then we can think of \(A\) as a function of \(B\) and write
\(\displaystyle A=0.4B+12\)
or we can think of \(B\) as a function of \(A\) and write
\(\displaystyle B=2.5A-30\)