Lesson 12
How Much Will Fit?
12.1: Two Containers (5 minutes)
Warm-up
In the previous lesson, students studied the relationship between volume of liquid and the height of the liquid when poured into a cylindrical container. The purpose of this warm-up is to shift students’ attention toward other types of containers and to consider how the volume of two containers differs. This warm-up is direct preparation for the first activity of the lesson in which students reason about volumes of several container types and re-familiarize themselves with the language of three-dimensional objects.
Launch
Tell students to close their books or devices. Arrange students in groups of 2. Display the image of the two containers filled with beans for all to see.

Give partners 1 minute to estimate how many beans are in each container. Poll the class for their estimates and display these values for all to see, in particular the range of values expressed.
Tell students that the smaller container holds 200 beans. Ask students to open their books or devices and reconsider their estimate for the large container now that they have more information. Give 1–2 minutes for students to write down a new estimate. Follow with a whole-class discussion.
Student Facing
Your teacher will show you some containers. The small container holds 200 beans. Estimate how many beans the large jar holds.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may not be sure how to start estimating the amount of beans in the larger jar once the number of beans in the smaller jar is known. Encourage them to start by estimating how the dimensions (e.g., height, width) of the two containers compare. For example, since the larger jar is more than twice the height of the smaller and has a greater width, then it must have at least twice as many beans.
Activity Synthesis
Poll the class for their new estimates for the number of beans in the larger container and display these next to the original estimates for all to see. Tell the class that the large container actually holds about 1,000 beans.
Discuss:
- “How did you and your partner calculate your estimate for the large jar?” (We estimated the large jar holds 900 beans since the large jar is about 3 times taller than the smaller jar, and it’s about 1.5 times wider and \(200\boldcdot 3\boldcdot 1.5=900\).)
- “Is there a more accurate way to measure the difference in volume between the two containers than ‘number of beans.’” (Yes, we could use something smaller than beans so there is less air, such as rice or water.)
- “What are some examples of units used to measure volume? Where have you seen them used in your life?” (Cups, tablespoons, gallons, liters, cubic centimeters, etc. Drinks often have fluid ounces, gallons, or liters written on them. Recipes may use cups or tablespoons.)
12.2: What’s Your Estimate? (15 minutes)
Activity
The purpose of this activity is for students to practice using precise language to describe how they estimated volumes of objects. Starting from an object of known volume, students must consider the difference in dimensions between the two objects. The focus here is on strategies to estimate the volume and units of measure used, not on exact answers or calculating volume using a formula (which will be the focus of later lessons). Notice students who:
- have clear strategies to estimate volume of contents inside container
- have an estimate that is very close to the actual volume
Launch
Arrange students in groups of 2.
Option 1: Bring in real containers and have students estimate how much rice each would hold, one at a time, preferably with one container whose volume is stated so students have a visual reference for their estimates. Also bring plenty of dried rice and measuring tools, such as tablespoons or cups. After collecting students’ estimates, you can demonstrate how much rice each container holds using whichever units of measure the class deems reasonable. Note that 1 tablespoon is 0.5 ounces or around 15 milliliters. 1 cup is 8 ounces or around 240 milliliters. 1 milliliter is the same as 1 cubic centimeter.
Option 2: Display images one at a time for all to see. Give students 1–2 minutes to work with their partner and write down an estimate for the objects of unknown volumes in the picture. Follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
Your teacher will show you some containers.
- If the pasta box holds 8 cups of rice, how much rice would you need for the other rectangular prisms?
- If the pumpkin can holds 15 fluid ounces of rice, how much do the other cylinders hold?
- If the small cone holds 2 fluid ounces of rice, how much does the large cone hold?
- If the golf ball were hollow, it would hold about 0.2 cups of water. If the baseball were hollow, how much would the sphere hold?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think there is a single right answer. Measurements are always approximate. Some of the measurements given by the authors of this activity were calculated using estimates from the photos, and may not be very precise. Measurements listed on the sides of packages are more accurate, but actual contents may vary slightly.
Activity Synthesis
For each set of containers, display the image and select previously identified students to share their strategies for estimating the volume. Once strategies for each set of containers are shared, discuss:
- “How do the estimates differ if we measure using water verses rice?” (Measuring with rice leaves a bit of empty space between the grains, while water, being liquid, leaves no empty space, so it’s more accurate.)
- “If the containers we used were much larger (like a water tank), would our units of measure change? Why?” (If we were measuring larger volumes, we might want to use a larger unit, like gallons. 4000 ml sounds big, but it’s only a bit more than 1 gallon, which isn’t that much water.)
Conclude the discussion by asking students to compare some other units of measure for volume that they know of. Have students recall what they know about unit conversion between some units of measure. Example:
- Fluid ounces, quarts, cups, liters, milliliters
- Cubic feet, cubic meters, cubic yards
- Note that cubic centimeters are special, because 1 cc = 1 ml
If it comes up, here is the scoop on ounces: units called “ounces” are used to measure both volume and weight. It is important to be clear about what quantity you are measuring! To differentiate between them, people refer to the units of measure for volume as “fluid ounces.” For water, 1 fluid ounce is very close to 1 ounce by weight. This is not true for other substances! For example, mercury is much denser than water. 1 fluid ounce of mercury weighs about 13.6 ounces! Motor oil is less dense than water (that’s why it floats), so 1 fluid ounce of oil weighs only about 0.8 ounces. The metric system is not so confusing for quantities that would be measured in ounces, since it’s common to measure mass instead of weight and measure it in grams, whereas volume is measured in milliliters.
Design Principle(s): Support sense-making
12.3: Do You Know These Figures? (10 minutes)
Activity
The purpose of this activity is for students to learn or remember the names of the figures they worked with in the previous activity and learn a quick method for sketching a cylinder. Students start by determining the shapes that are the faces of the four shapes. They also determine which shape would be considered the base of each figure shown. This allows students to connect previously learned two-dimensional figures to new three-dimensional figures introduced here. The last question introduces students to a way to sketch a cylinder. This is a skill they will continue to use throughout the unit when working on problems that do not provide a visual example of a situation. Identify students who sketch cylinders that are different sizes or drawn sideways.
Launch
It is strongly recommended that you provide physical, solid objects for students to hold and look at. If using physical objects, pass around the objects for students to see and feel before starting the activity.
Give students 3–5 minutes of quiet work time, followed by a whole-class discussion.
Student Facing
- What shapes are the faces of each type of object shown here? For example, all six faces of a cube are squares.

- Which faces could be referred to as a “base” of the object?
- Here is a method for quickly sketching a cylinder:
- Draw two ovals.
- Connect the edges.
- Which parts of your drawing would
be hidden behind the cylinder?
Make these parts dashed lines.
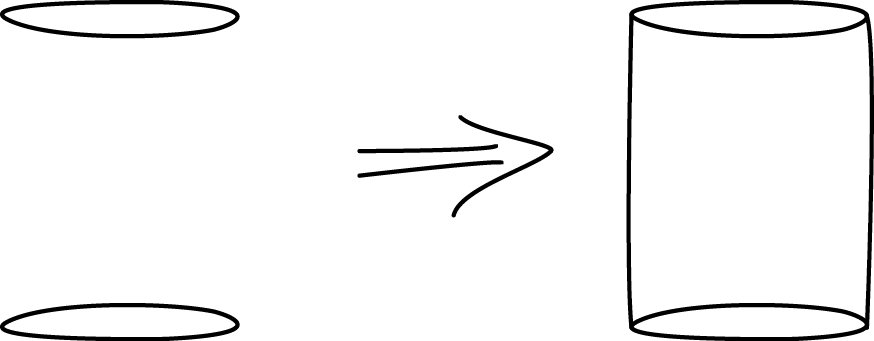
- Practice sketching some cylinders. Sketch a few different sizes, including short, tall, narrow, wide, and sideways. Label the radius \(r\) and height \(h\) on each cylinder.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?

A soccer ball is a polyhedron with 12 black pentagonal faces and 20 white hexagonal faces. How many edges in total are on this polyhedron?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to visualize the shapes of the faces, position the object so that students can only see two dimensions. Ask students what two-dimensional shape they see.
Activity Synthesis
If using physical objects, display each object one at a time for all to see. If using images, display the images for all to see, and refer to each object one at a time. Ask students to identify:
- which figure the object is an example of
- the different shapes that make up the faces of the figure
- the shape that is the base of the figure
Select previously identified students to share their sketches of cylinders. The goal is to ensure that students see a variety of cylinders: short, tall, sideways, narrow, etc. If no student drew a “sideways” cylinder, sketch one for all to see and make sure students understand that even though it is sideways, the height is still the length perpendicular to the base.
Tell students that we will be working with these different three-dimensional figures for the rest of this unit. Consider posting a display in the classroom that shows a diagram of each object labeled with its name, and where appropriate, with one side labeled “base.” As volume formulas are developed, the formulas can be added to the display.
Design Principle(s): Optimize output (for comparison); Cultivate conversation
Lesson Synthesis
Lesson Synthesis
The volume of a three-dimensional figure is the amount of space it encloses. Ask students:
- “What are some shapes you worked with in today’s lesson?” (Cylinders, cones, spheres, rectangular prisms)
- “What are some different units of measure we use to calculate volume of these figures?” (Cubic feet, fluid ounces, gallons, cubic nanometers, rice)
- “What are some examples of objects we see in our world that are very similar to these figures that you didn't see in the pictures earlier?” (A basketball is like a sphere. A cell phone is like a rectangular prism.)
12.4: Cool-down - Rectangle to Round (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The volume of a three-dimensional figure, like a jar or a room, is the amount of space the shape encloses. We can measure volume by finding the number of equal-sized volume units that fill the figure without gaps or overlaps. For example, we might say that a room has a volume of 1,000 cubic feet, or that a pitcher can carry 5 gallons of water. We could even measure volume of a jar by the number of beans it could hold, though a bean count is not really a measure of the volume in the same way that a cubic centimeter is because there is space between the beans. (The number of beans that fit in the jar do depend on the volume of the jar, so it is an okay estimate when judging the relative sizes of containers.)
In earlier grades, we studied three-dimensional figures with flat faces that are polygons. We learned how to calculate the volumes of rectangular prisms. Now we will study three-dimensional figures with circular faces and curved surfaces: cones, cylinders, and spheres.
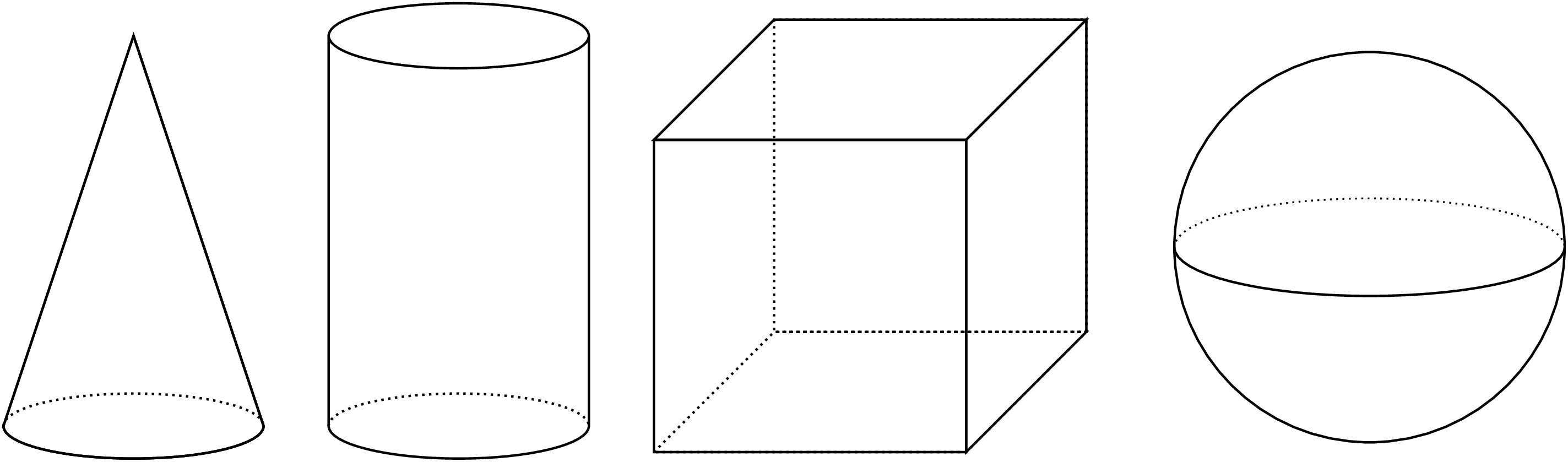
To help us see the shapes better, we can use dotted lines to represent parts that we wouldn't be able to see if a solid physical object were in front of us. For example, if we think of the cylinder in this picture as representing a tin can, the dotted arc in the bottom half of that cylinder represents the back half of the circular base of the can. What objects could the other figures in the picture represent?



