Lesson 7

Connecting Representations of Functions

7.1: Which are the Same? Which are Different? (5 minutes)

The purpose of this warm-up is for students to identify connections between three different representations of functions: equation, graph, and table. Two of the functions displayed are the same but with different variable names. It is important for students to focus on comparing input-output pairs when deciding how two functions are the same or different.

Give students 1–2 minutes of quiet work time followed by a whole-class discussion.

Here are three different ways of representing functions. How are they alike? How are they different?

\(\displaystyle y = 2x\)

Coordinate plane, horizontal, a, negative 4 to 4 by ones, vertival, b, negative 4 to 4 by ones. A line goes through the origin and the labeled point (1 comma 2).

\(p\)	-2	-1	0	1	2	3
\(q\)	4	2	0	-2	-4	-6

For access, consult one of our IM Certified Partners.

Ask students to share ways the representations are alike and different. Record and display the responses for all to see. To help students clarify their thinking, ask students to reference the equation, graph, or table when appropriate. If the relationship between the inputs and outputs in each representation does not arise, ask students what they notice about that relationship in each representation.

7.2: Comparing Temperatures (10 minutes)

This is the first of three activities where students make connections between different functions represented in different ways. In this activity, students are given a graph and a table of temperatures from two different cities and are asked to make sense of the representations in order to answer questions about the context.

Arrange students in groups of 2. Give students 3–5 minutes of quiet work time and then time to share responses with their partner. Follow with a whole-class discussion.

Representation: Internalize Comprehension. Demonstrate and encourage students to use color coding and annotations to highlight connections between representations in a problem. For example, ask students to use the same color to highlight the temperatures for each city that occurred at the same time such as blue for 4:00 pm.
Supports accessibility for: Visual-spatial processing

Writing, Conversing: MLR5 Co-Craft Questions. Display the graph and table to students without revealing the questions that follow. Invite students to work with their partner to write possible questions that could be answered by the two different representations for the two cities. Select 2–3 groups to share their questions with the class. Highlight questions that invite comparisons between the two cities. This helps students produce the language of mathematical questions and talk about the relationships between the graph and table.
Design Principle(s): Maximize meta-awareness; Support sense-making

The graph shows the temperature between noon and midnight in City A on a certain day.

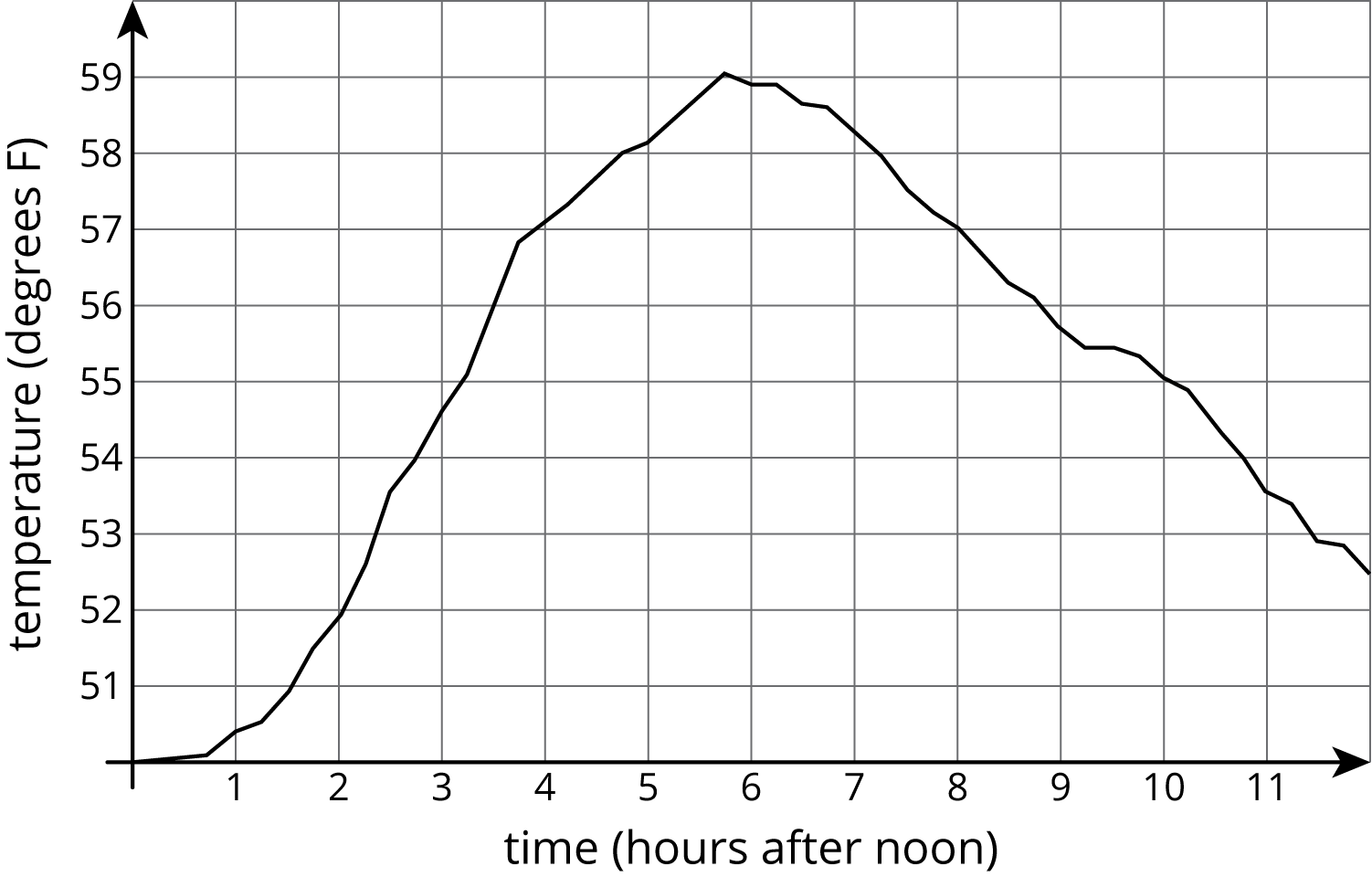
The table shows the temperature, \(T\), in degrees Fahrenheit, for \(h\) hours after noon, in City B.

\(h\)	1	2	3	4	5	6
\(T\)	82	78	75	62	58	59

Which city was warmer at 4:00 p.m.?
Which city had a bigger change in temperature between 1:00 p.m. and 5:00 p.m.?
How much greater was the highest recorded temperature in City B than the highest recorded temperature in City A during this time?
Compare the outputs of the functions when the input is 3.

For access, consult one of our IM Certified Partners.

Display the graph and table for all to see. Select groups to share how they used the two different representations to get their answers for each question. To further student thinking about the advantages and disadvantages of each representation, ask:

“Which representation do you think is better for identifying the highest recorded temperature in a city?” (The graph, since I just have to find the highest part. In the table I have to read all the values in order to find the highest temperature.)
“Which representation do you think is quicker for figuring out the change in temperature between 1:00 p.m. and 5:00 p.m.?” (The table was quicker since the numbers are given and I only have to subtract. In the graph I had to figure out the temperature values for both times before I could subtract.)

7.3: Comparing Volumes (10 minutes)

This is the second of three activities where students make connections between different functions represented in different ways. In this activity, students are given an equation and a graph of the volumes of two different objects. Students then compare inputs and outputs of both functions and what those values mean in the context of the shapes.

Digital

Arrange students in groups of 2. Give students 3–5 minutes of quiet work time and then time to share their responses with their partner. Follow with a whole-class discussion.

If using the digital activity, students will have an interactive version of the graph that the print statement uses. Using this version, students can click on the graph to determine coordinates, which might be helpful. The focus of the discussion should remain on how and why students used the graph and equation.

Representation: Develop Language and Symbols. Use virtual or concrete manipulatives to connect symbols to concrete objects or values. For example show or provide students with a cube and sphere. Discuss the relationship between the side length or radius and the volume of the object.
Supports accessibility for: Conceptual processing

The volume, \(V\), of a cube with edge length \(s\) cm is given by the equation \(V = s^3\). The volume of a sphere is a function of its radius (in centimeters), and the graph of this relationship is shown here.

Is the volume of a cube with edge length \(s=3\) greater or less than the volume of a sphere with radius 3?
If a sphere has the same volume as a cube with edge length 5, estimate the radius of the sphere.
Compare the outputs of the two volume functions when the inputs are 2.

Here is an applet to use if you choose.

For access, consult one of our IM Certified Partners.

Arrange students in groups of 2. Give students 3–5 minutes of quiet work time and then time to share their responses with their partner. Follow with a whole-class discussion.

The volume, \(V\), of a cube with edge length \(s\) cm is given by the equation \(V = s^3\).

The volume of a sphere is a function of its radius (in centimeters), and the graph of this relationship is shown here.

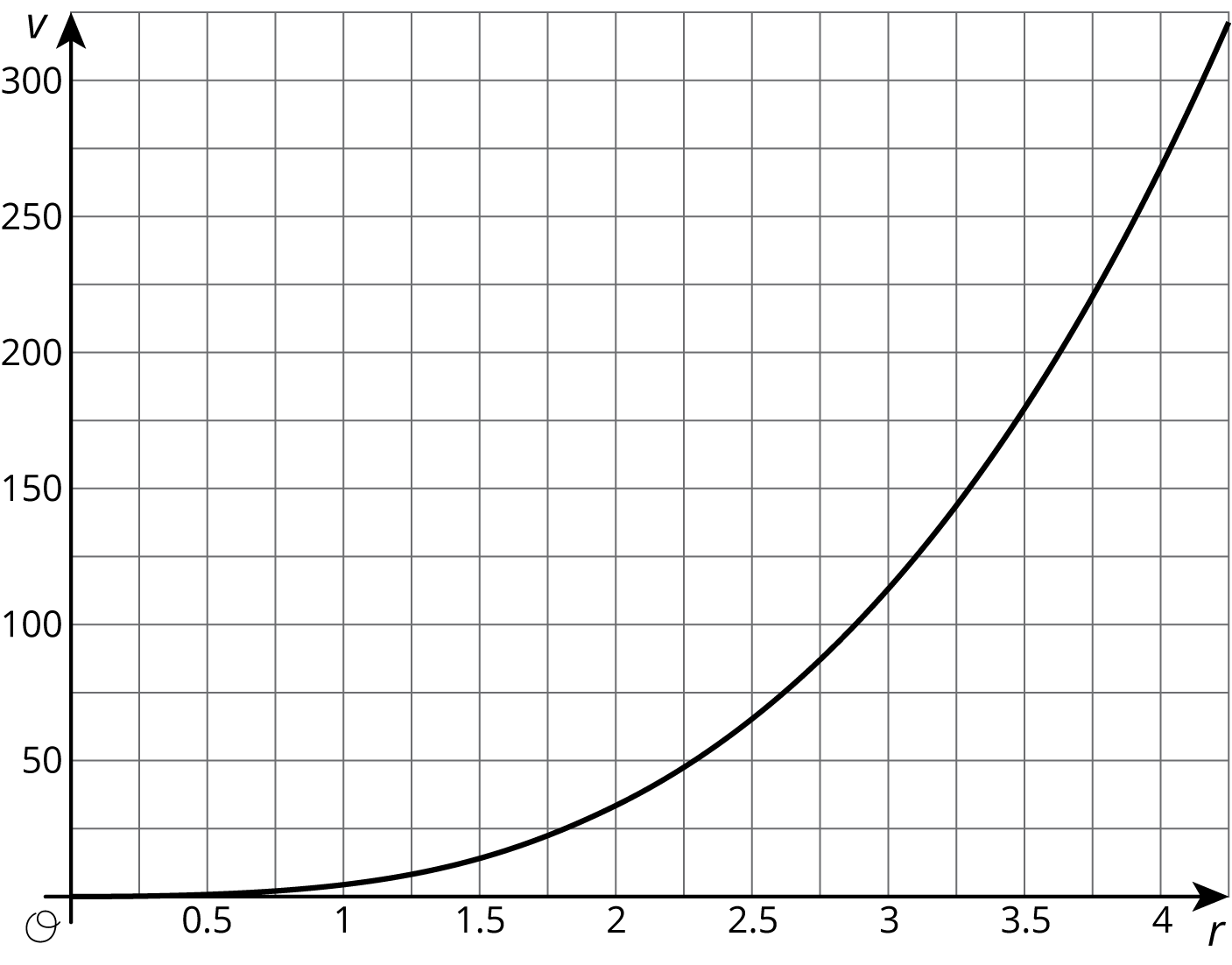
Coordinate plane, horizontal, r, 0 to 4 by point fives. Vertical, v, 0 to 300 by fifties. Curve begins at origin, rises slowly, roughly (2 point 2 5 comma 33), more quickly to (3 point 5 comma 180).

Is the volume of a cube with edge length \(s=3\) greater or less than the volume of a sphere with radius 3?
If a sphere has the same volume as a cube with edge length 5, estimate the radius of the sphere.
Compare the outputs of the two volume functions when the inputs are 2.

For access, consult one of our IM Certified Partners.

Are you ready for more?

Estimate the edge length of a cube that has the same volume as a sphere with radius 2.5.

For access, consult one of our IM Certified Partners.

Some students may struggle with the many parts of the second question. These two questions can help scaffold the question for students who need it:

“What information is given to you and what can you do with it?”
“What information is the focus of the question and what would you like to know to be able to answer that question.”

The purpose of this discussion is for students to think about how they used the information from the different representations to answer questions around the context.

Display the equation and graph for all to see. Invite groups to share how they used the representations to answer the questions. Consider asking the following questions to have students expand on their answers:

“How did you use the given representations to find an answer? How did you use the equation? The graph?”
“For which problems was it nicer to use the equation? The graph? Explain your reasoning.”

Conversing, Representing, Writing: MLR2 Collect and Display. As students work, capture the vocabulary and phrases students use to describe the connections across the two different representations (e.g., equation and graph). Listen for students who justify their ideas by explaining how or why they know something is true based on the equation or graph. Scribe students’ language on a visual display that can be referenced in future discussions. This will help students to produce and make sense of the language needed to communicate about the relationships between quantities represented by functions graphically and in equations.
Design Principle(s): Support sense-making; Maximize meta-awareness

7.4: It’s Not a Race (10 minutes)

In this activity, students continue their work comparing properties of functions represented in different ways. Students are given a verbal description and a table to compare and decide whose family traveled farther over the same time intervals. The purpose of this activity is for students to continue building their skill interpreting and comparing functions.

Give students 3–5 minutes of quiet work time, followed with whole-class discussion.

Elena’s family is driving on the freeway at 55 miles per hour.

Andre’s family is driving on the same freeway, but not at a constant speed. The table shows how far Andre's family has traveled, \(d\), in miles, every minute for 10 minutes.

\(t\)	1	2	3	4	5	6	7	8	9	10
\(d\)	0.9	1.9	3.0	4.1	5.1	6.2	6.8	7.4	8	9.1

How many miles per minute is 55 miles per hour?
Who had traveled farther after 5 minutes? After 10 minutes?
How long did it take Elena’s family to travel as far as Andre’s family had traveled after 8 minutes?
For both families, the distance in miles is a function of time in minutes. Compare the outputs of these functions when the input is 3.

For access, consult one of our IM Certified Partners.

Students may miss that Elena’s family’s speed has different units than what is needed to compare with Andre’s family. Point out to students that the units are important and possibly ask them to find out how many miles Elena’s family travels in 1 minute rather than 1 hour.

The purpose of this discussion is for students to think about how they use a verbal description and table to answer questions related to the context. Ask students to share their solutions and how they used the equation and graph. Consider asking some of the following questions:

“How did you use the table to get information? How did you use the verbal description?”
“What did you prefer about using the description to solve the problem? What did you prefer about using the table to solve the problem?”

Engagement: Develop Effort and Persistence. Break the class into small discussion groups and then invite a representative from each group to report back to the whole class.
Supports accessibility for: Language; Social-emotional skills; Attention

Writing, Speaking: MLR1 Stronger and Clearer Each Time. Use this routine to give students a structured opportunity to reflect on their problem-solving strategies. Ask students to write an initial response to the prompt, “What did you prefer about using the description to solve the problem? What did you prefer about using the table to solve the problem?” Give students time to meet with 2–3 partners, to share and get feedback on their responses. Provide prompts for feedback that will help students strengthen their ideas and clarify their language (e.g., “What do you mean?”, “Can you give an example?”, and “Can you say that another way?”, etc.). Give students 1–2 minutes to revise their writing based on the feedback they received. This will help students produce a written generalization about interpreting and comparing functions.
Design Principle(s): Optimize output (for generalization)

Lesson Synthesis

We looked at several different ways functions are represented today: graphs, tables, equations, and verbal descriptions. We can use each representation to find outputs for different inputs. In each case we may perform different actions, but we are looking for the same information. Consider discussing these questions to emphasize the strengths and weaknesses of the representations with students:

“Think about each of the representations of a function that we have used today. What is easy or hard about using each representation? What type of question do you prefer to answer with each?”
“If we had only used tables in the volume activity, how could that have made it easier? Harder?” (It would have been easier to find the volumes when the inputs were the same value, but it would have been harder if the tables didn't have exactly the same inputs.)
“If we had only used graphs to represent the functions in the car activity, how would that have been easier? How would it have been harder?” (It is easier to compare which is farther at a specific time, but it is harder to have an accurate answer, since graphs require estimation.)

7.5: Cool-down - Comparing Different Areas (5 minutes)

For access, consult one of our IM Certified Partners.

Student Lesson Summary

Functions are all about getting outputs from inputs. For each way of representing a function—equation, graph, table, or verbal description—we can determine the output for a given input.

Let's say we have a function represented by the equation \(y = 3x +2\) where \(y\) is the dependent variable and \(x\) is the independent variable. If we wanted to find the output that goes with 2, we can input 2 into the equation for \(x\) and finding the corresponding value of \(y\). In this case, when \(x\) is 2, \(y\) is 8 since \(3\boldcdot 2 + 2=8\).

If we had a graph of this function instead, then the coordinates of points on the graph are the input-output pairs. So we would read the \(y\)-coordinate of the point on the graph that corresponds to a value of 2 for \(x\). Looking at the graph of this function here, we can see the point \((2,8)\) on it, so the output is 8 when the input is 2.

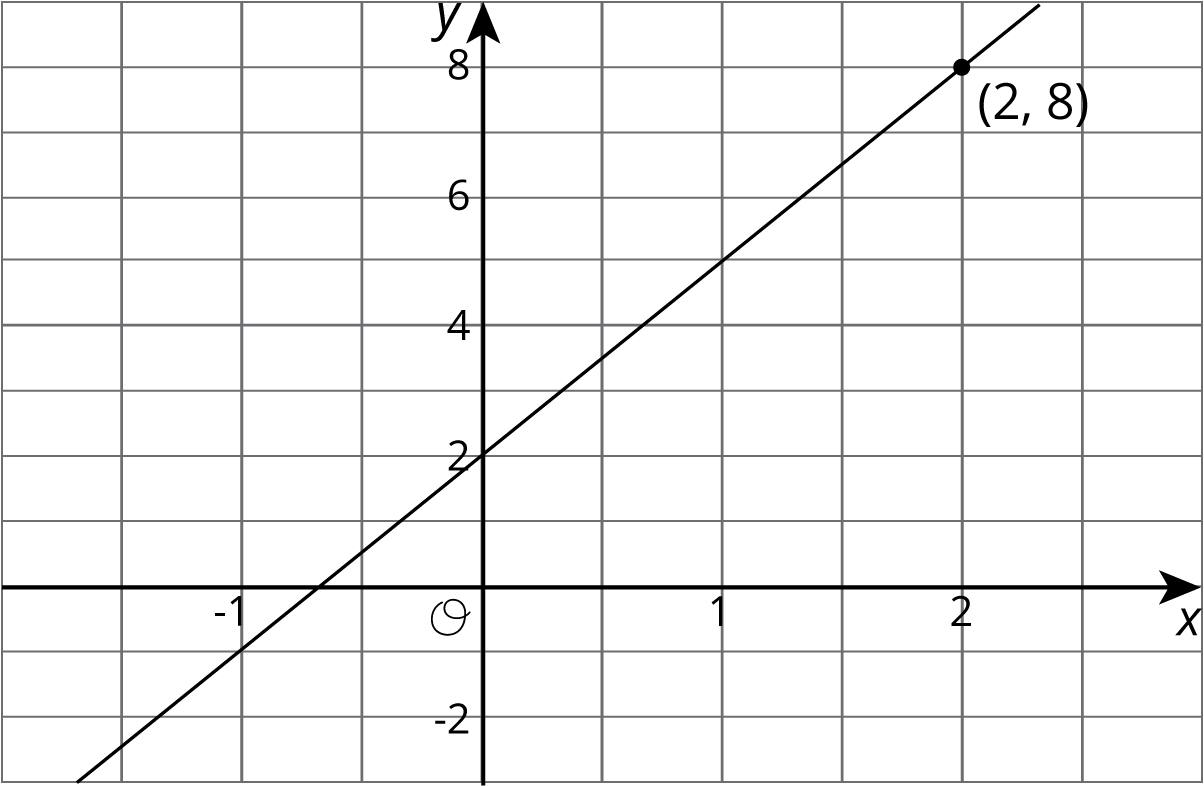
Coordinate plane, x, negative 1 to 2 by ones, y negative 2 to 8 by twos. Graph on a straight line through (0 comma 2), and (2 comma 8).

A table representing this function shows the input-output pairs directly (although only for select inputs).

\(x\)	-1	0	1	2	3
\(y\)	-1	2	5	8	11

Again, the table shows that if the input is 2, the output is 8.

Video Summary

Video VLS G8U5V2 Representing and Interpreting Functions (Lessons 4–7) available at https://player.vimeo.com/video/498502033.

Lesson 7

7.1: Which are the Same? Which are Different? (5 minutes)

Warm-up

Launch

Student Facing

Student Response

Activity Synthesis

7.2: Comparing Temperatures (10 minutes)

Activity

Launch

Student Facing

Student Response

Activity Synthesis

7.3: Comparing Volumes (10 minutes)

Activity

Launch

Student Facing

Student Response

Launch

Student Facing

Student Response

Student Facing

Are you ready for more?

Student Response

Anticipated Misconceptions

Activity Synthesis

7.4: It’s Not a Race (10 minutes)

Optional activity

Launch

Student Facing

Student Response

Anticipated Misconceptions

Activity Synthesis

Lesson Synthesis

Lesson Synthesis

7.5: Cool-down - Comparing Different Areas (5 minutes)

Cool-Down

Student Lesson Summary

Student Facing

Video Summary

Student Facing