Lesson 16
Finding the Percentage
Let’s find percentages in general.
16.1: True or False: Percentages
Is each statement true or false? Be prepared to explain your reasoning.
- 25% of 512 is equal to \(\frac14 \boldcdot 500\).
- 90% of 133 is equal to \((0.9) \boldcdot 133\).
- 30% of 44 is equal to 3% of 440.
- The percentage 21 is of 28 is equal to the percentage 30 is of 40.
16.2: Jumping Rope
A school held a jump-roping contest. Diego jumped rope for 20 minutes.
-
Jada jumped rope for 15 minutes. What percentage of Diego’s time is that?
-
Lin jumped rope for 24 minutes. What percentage of Diego’s time is that?
-
Noah jumped rope for 9 minutes. What percentage of Diego’s time is that?
- Record your answers in this table. Write the quotients in the last column as decimals.
time (minutes) percentage \(\text{time} \div 20\) Diego 20 100 \(\frac{20}{20} = 1\text{ }\) Jada 15 \(\frac{15}{20} = \text{ }\) Lin 24 \(\frac{24}{20} = \text{ }\) Noah 9 \(\frac{9}{20} = \text{ }\) - What do you notice about the numbers in the last two columns of the table?
16.3: Restaurant Capacity
A restaurant has a sign by the front door that says, “Maximum occupancy: 75 people.” Answer each question and explain or show your reasoning.
- What percentage of its capacity is 9 people?
- What percentage of its capacity is 51 people?
- What percentage of its capacity is 84 people?
Water makes up about 71% of Earth’s surface, while the other 29% consists of continents and islands. 96% of all Earth’s water is contained within the oceans as salt water, while the remaining 4% is fresh water located in lakes, rivers, glaciers, and the polar ice caps.
If the total volume of water on Earth is 1,386 million cubic kilometers, what is the volume of salt water? What is the volume of fresh water?
Summary
What percentage of 90 kg is 36 kg? One way to solve this problem is to first find what percentage 1 kg is of 90, and then multiply by 36.
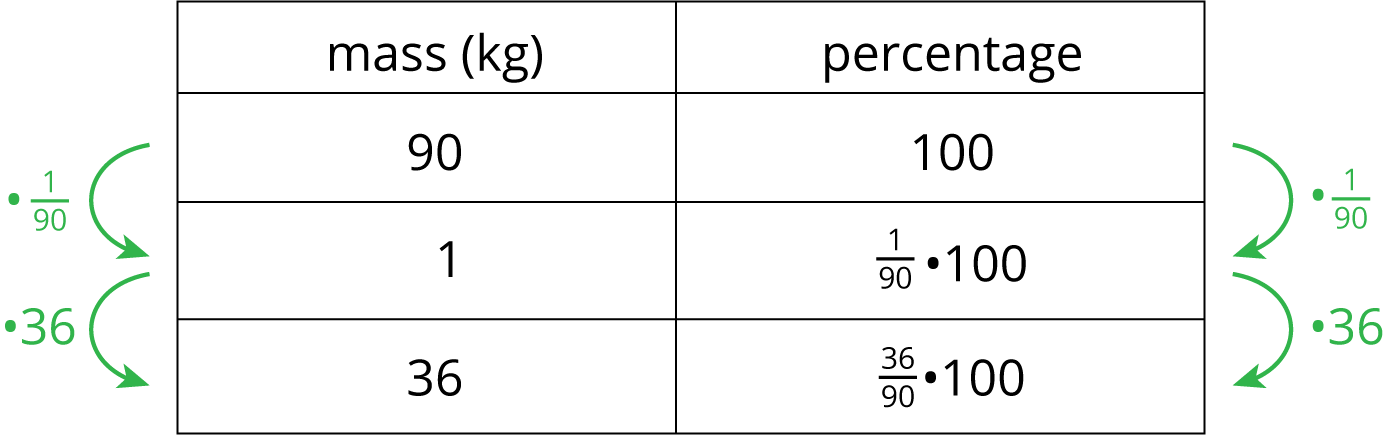
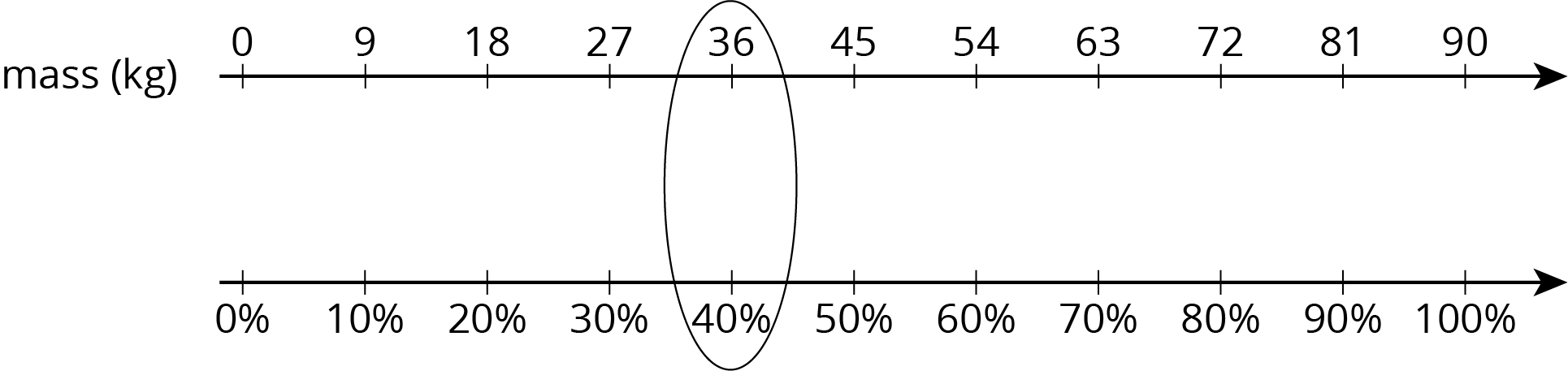
From the table we can see that 1 kg is \(\left(\frac{1}{90}\boldcdot 100\right) \%\), so 36 kg is \(\left(\frac{36}{90}\boldcdot 100\right) \%\) or 40% of 90. We can confirm this on a double number line:
In general, to find what percentage a number \(C\) is of another number \(B\) is to calculate \(\frac{C}{B}\) of 100%. We can find that by multiplying: \(\displaystyle \frac{C}{B}\boldcdot 100 \)
Suppose a school club has raised \$88 for a project but needs a total of \$160. What percentage of its goal has the club raised?
To find what percentage \$88 is of \$160, we find \(\frac {88}{160}\) of 100% or \(\frac {88}{160} \boldcdot 100\), which equals \( \frac {11}{20} \boldcdot 100\) or 55. The club has raised 55% of its goal.
Video Summary
Glossary Entries
- percent
The word percent means “for each 100.” The symbol for percent is %.
For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.


- percentage
A percentage is a rate per 100.
For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.
