Lesson 13
Benchmark Percentages
Let’s contrast percentages and fractions.
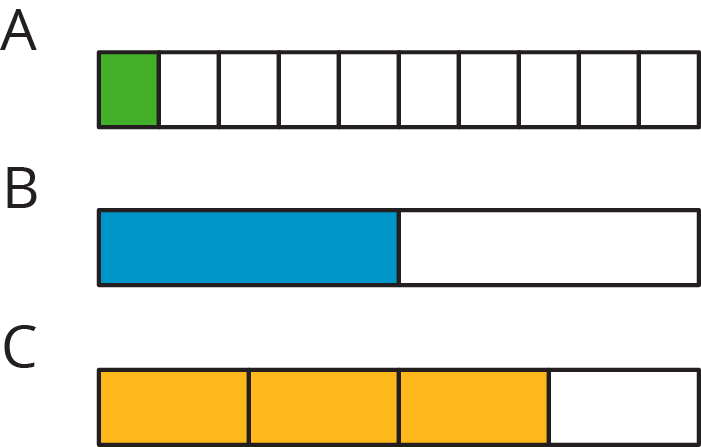
13.1: What Percentage Is Shaded?
What percentage of each diagram is shaded?
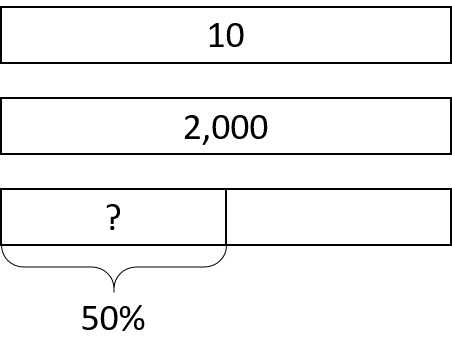
13.2: Liters, Meters, and Hours
-
- How much is 50% of 10 liters of milk?
- How far is 50% of a 2,000-kilometer trip?
- How long is 50% of a 24-hour day?
- How can you find 50% of any number?
-
- How far is 10% of a 2,000-kilometer trip?
- How much is 10% of 10 liters of milk?
- How long is 10% of a 24-hour day?
- How can you find 10% of any number?
-
- How long is 75% of a 24-hour day?
- How far is 75% of a 2,000-kilometer trip?
- How much is 75% of 10 liters of milk?
- How can you find 75% of any number?
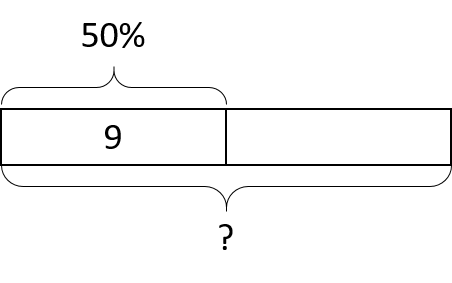
13.3: Nine is . . .
Explain how you can calculate each value mentally.
- 9 is 50% of what number?
- 9 is 25% of what number?
- 9 is 10% of what number?
- 9 is 75% of what number?
- 9 is 150% of what number?
13.4: Matching the Percentage
Match the percentage that describes the relationship between each pair of numbers. One percentage will be left over. Be prepared to explain your reasoning.
-
7 is what percentage of 14?
-
5 is what percentage of 20?
-
3 is what percentage of 30?
-
6 is what percentage of 8?
-
20 is what percentage of 5?
- 4%
- 10%
- 25%
- 50%
- 75%
- 400%
- What percentage of the world’s current population is under the age of 14?
- How many people is that?
- How many people are 14 or older?
Summary
Certain percentages are easy to think about in terms of fractions.
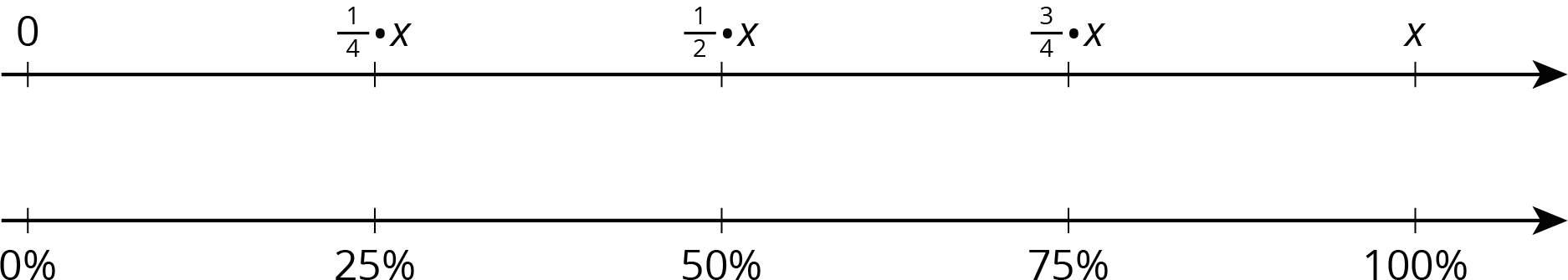
- 25% of a number is always \(\frac14\) of that number.
For example, 25% of 40 liters is \(\frac14 \boldcdot 40\) or 10 liters. - 50% of a number is always \(\frac12\) of that number.
For example, 50% of 82 kilometers \(\frac12 \boldcdot 82\) or 41 kilometers. - 75% of a number is always \(\frac34\) of that number.
For example, 75% of 1 pound is \(\frac34\) pound. - 10% of a number is always \(\frac{1}{10}\) of that number.
For example, 10% of 95 meters is 9.5 meters. - We can also find multiples of 10% using tenths.
For example, 70% of a number is always \(\frac{7}{10}\) of that number, so 70% of 30 days is \(\frac{7}{10} \boldcdot 30\) or 21 days.

Video Summary
Glossary Entries
- percent
The word percent means “for each 100.” The symbol for percent is %.
For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.


- percentage
A percentage is a rate per 100.
For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.
