Lesson 9

Linear Models

Let’s model situations with linear functions.

Problem 1

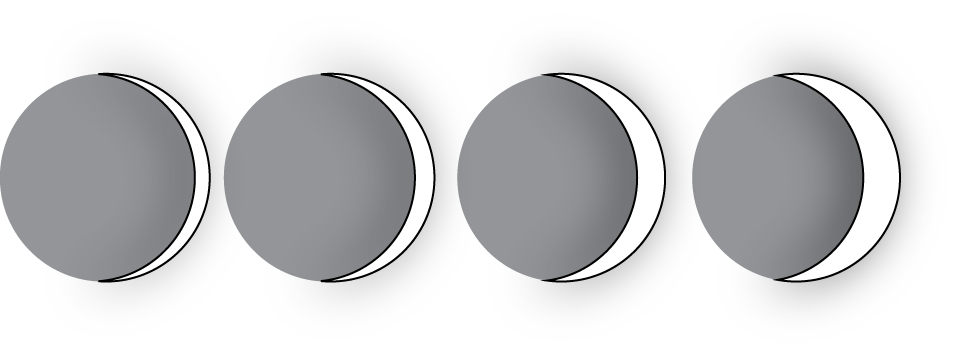
Four images of the moon, each with a larger crescent illuminated.

On the first day after the new moon, 2% of the Moon's surface is illuminated. On the second day, 6% is illuminated.

  1. Based on this information, predict the day on which the Moon’s surface is 50% illuminated and 100% illuminated.

  2. The Moon’s surface is 100% illuminated on day 14. Does this agree with the prediction you made?

  3. Is the percentage illumination of the Moon’s surface a linear function of the day?

Problem 2

In science class, Jada uses a graduated cylinder with water in it to measure the volume of some marbles. After dropping in 4 marbles so they are all under water, the water in the cylinder is at a height of 10 milliliters. After dropping in 6 marbles so they are all under water, the water in the cylinder is at a height of 11 milliliters.

  1. What is the volume of 1 marble?
  2. How much water was in the cylinder before any marbles were dropped in?
  3. What should be the height of the water after 13 marbles are dropped in?
  4. Is the relationship between volume of water and number of marbles a linear relationship? If so, what does the slope of a line representing this relationship mean? If not, explain your reasoning.

Problem 3

Solve each of these equations. Explain or show your reasoning.

\(2(3x+2)=2x+28\)

\(5y+13=\text-43-3y\)

\(4(2a+2)=8(2-3a)\)

 

(From Unit 4, Lesson 5.)

Problem 4

For a certain city, the high temperatures (in degrees Celsius) are plotted against the number of days after the new year. 

Based on this information, is the high temperature in this city a linear function of the number of days after the new year?

Coordinate plane, horizontal, negative 1 to 14 by ones, vertical, negative 4 to 16 by twos. Three points are drawn but not labeled, (1 comma negative 3), (3 comma 1), (10 comma 15).

Problem 5

The school designed their vegetable garden to have a perimeter of 32 feet with the length measuring two feet more than twice the width.

  1. Using \(\ell\) to represent the length of the garden and \(w\) to represent its width, write and solve a system of equations that describes this situation.

  2. What are the dimensions of the garden?

(From Unit 4, Lesson 15.)