Lesson 2

Introduction to Functions

Let’s learn what a function is.

2.1: Square Me

Here are some numbers in a list:

1, -3, \(\text-\frac12\), 3, 2, \(\frac14\), 0.5

  1. How many different numbers are in the list?

  2. Make a new list containing the squares of all these numbers.

  3. How many different numbers are in the new list?

  4. Explain why the two lists do not have the same number of different numbers.

2.2: You Know This, Do You Know That?

Say yes or no for each question. If yes, draw an input-output diagram. If no, give examples of two different outputs that are possible for the same input.

  1. A person is 5.5 feet tall. Do you know their height in inches?
     
  2. A number is 5. Do you know its square?
     

  3. The square of a number is 16. Do you know the number?
     

  4. A square has a perimeter of 12 cm. Do you know its area?
     

  5. A rectangle has an area of 16 cm2. Do you know its length?
     

  6. You are given a number. Do you know the number that is \(\frac15\) as big?
     

  7. You are given a number. Do you know its reciprocal?
     

2.3: Using Function Language

Here are the questions from the previous activity. For the ones you said yes to, write a statement like, “The height a rubber ball bounces to depends on the height it was dropped from” or “Bounce height is a function of drop height.” For all of the ones you said no to, write a statement like, “The day of the week does not determine the temperature that day” or “The temperature that day is not a function of the day of the week.”

  1. A person is 5.5 feet tall. Do you know their height in inches?
  2. A number is 5. Do you know its square?
  3. The square of a number is 16. Do you know the number?
  4. A square has a perimeter of 12 cm. Do you know its area?
  5. A rectangle has an area of 16 cm2. Do you know its length?
  6. You are given a number. Do you know the number that is \(\frac15\) as big?
  7. You are given a number. Do you know its reciprocal?

2.4: Same Function, Different Rule?

Which input-output rules could describe the same function (if any)? Be prepared to explain your reasoning.

Input-output rule diagram. Input, 7, right arrow, rule is, square it, right arrow, output, 49.
Input-output rule diagram. Input, 10, right arrow, rule is find the area given the side-length, right arrow, output, 100.
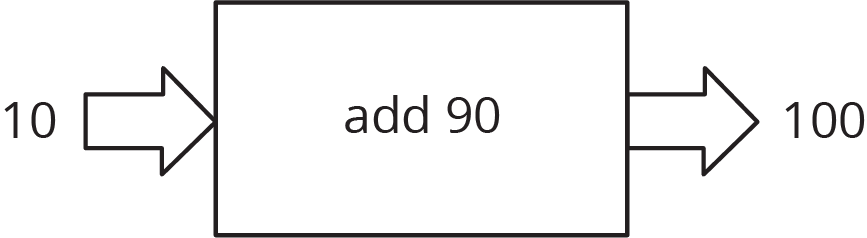
Input-output rule diagram. Input, 10, right arrow, rule is, add 90, right arrow, output, 100.

 



The phrase “is a function of” gets used in non-mathematical speech as well as mathematical speech in sentences like, “The range of foods you like is a function of your upbringing.” What is that sentence trying to convey? Is it the same use of the word “function” as the mathematical one?

Summary

Let's say we have an input-output rule that for each allowable input gives exactly one output. Then we say the output depends on the input, or the output is a function of the input.

For example, the area of a square is a function of the side length, because you can find the area from the side length by squaring it. So when the input is 10 cm, the output is 100 cm2.

Function rule diagram, input, 10, right arrow, rule given is, find the area of a square given the side-length, right arrow, output 100.

Sometimes we might have two different rules that describe the same function. As long as we always get the same, single output from the same input, the rules describe the same function.

Glossary Entries

  • function

    A function is a rule that assigns exactly one output to each possible input.

    The function \(y=6x+4\) assigns one value of the output, \(y\), to each value of the input, \(x\). For example, when \(x\) is 5, then \(y=6(5)+4\) or 34.