Lesson 5
More Graphs of Functions
Let’s interpret graphs of functions.
5.1: Which One Doesn’t Belong: Graphs
Which graph doesn’t belong?
5.2: Time and Temperature
The graph shows the temperature between noon and midnight in one day in a certain city.
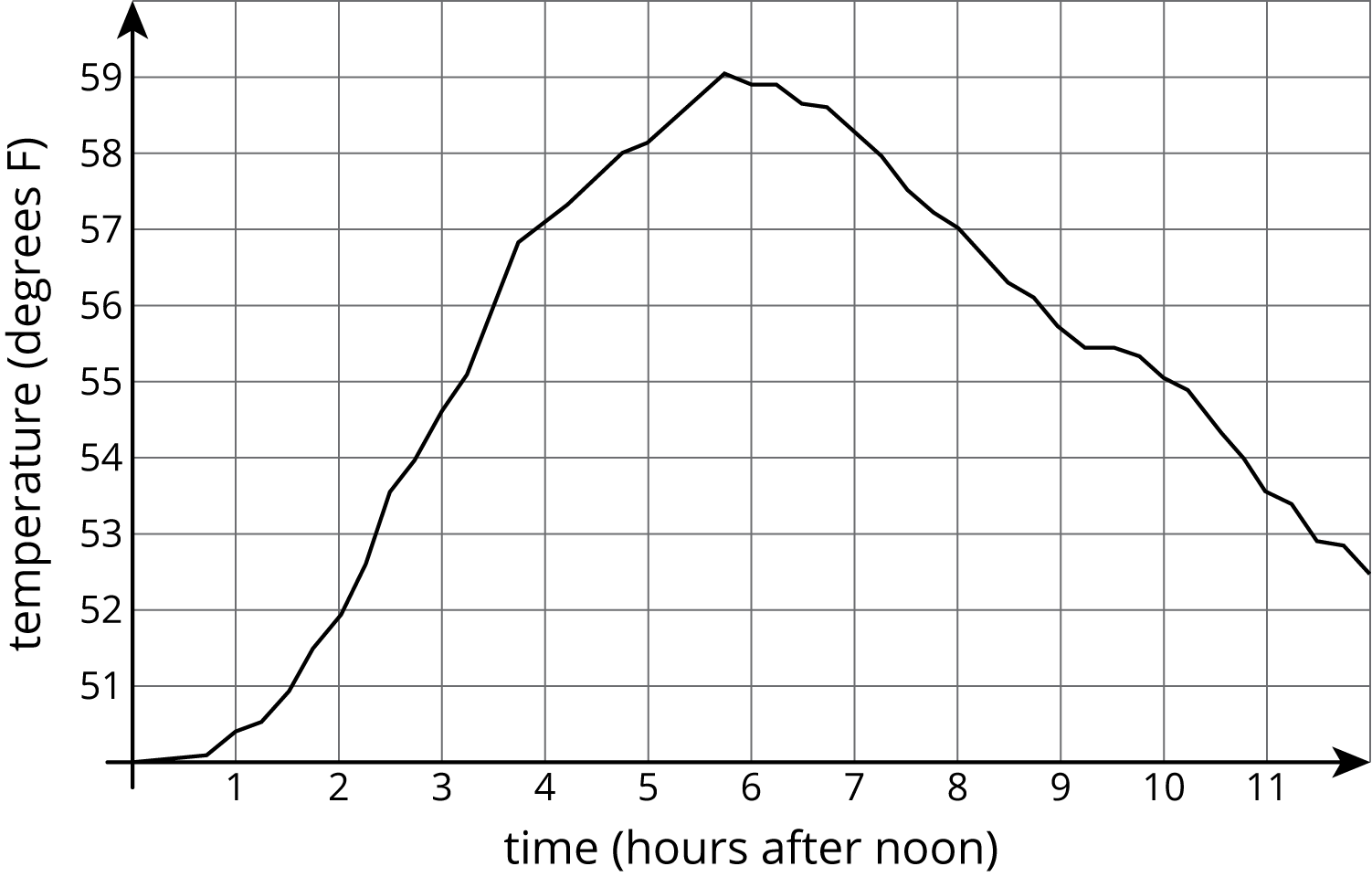
- Was it warmer at 3:00 p.m. or 9:00 p.m.?
- Approximately when was the temperature highest?
- Find another time that the temperature was the same as it was at 4:00 p.m.
- Did the temperature change more between 1:00 p.m. and 3:00 p.m. or between 3:00 p.m. and 5:00 p.m.?
- Does this graph show that temperature is a function of time, or time is a function of temperature?
- When the input for the function is 8, what is the output? What does that tell you about the time and temperature?
5.3: Garbage
- The graph shows the amount of garbage produced in the US each year between 1991 and 2013.

- Did the amount of garbage increase or decrease between 1999 and 2000?
- Did the amount of garbage increase or decrease between 2005 and 2009?
- Between 1991 and 1995, the garbage increased for three years, and then it decreased in the fourth year. Describe how the amount of garbage changed in the years between 1995 and 2000.

- The graph shows the percentage of garbage that was recycled between 1991 and 2013.

- When was it increasing?
- When was it decreasing?
- Tell the story of the change in the percentage of garbage recycled in the US over this time period.
Refer to the graph in the first part of the activity.
- Find a year where the amount of garbage produced increased from the previous year, but not by as much it increased the following year.
- Find a year where the amount of garbage produced increased from the previous year, and then increased by a smaller amount the following year.
- Find a year where the amount of garbage produced decreased from the previous year, but not by as much it decreased the following year.
-
Find a year where the amount of garbage produced decreased from the previous year, and then decreased by a smaller amount the following year.
Summary
Here is a graph showing the temperature in a town as a function of time after 8:00 p.m.
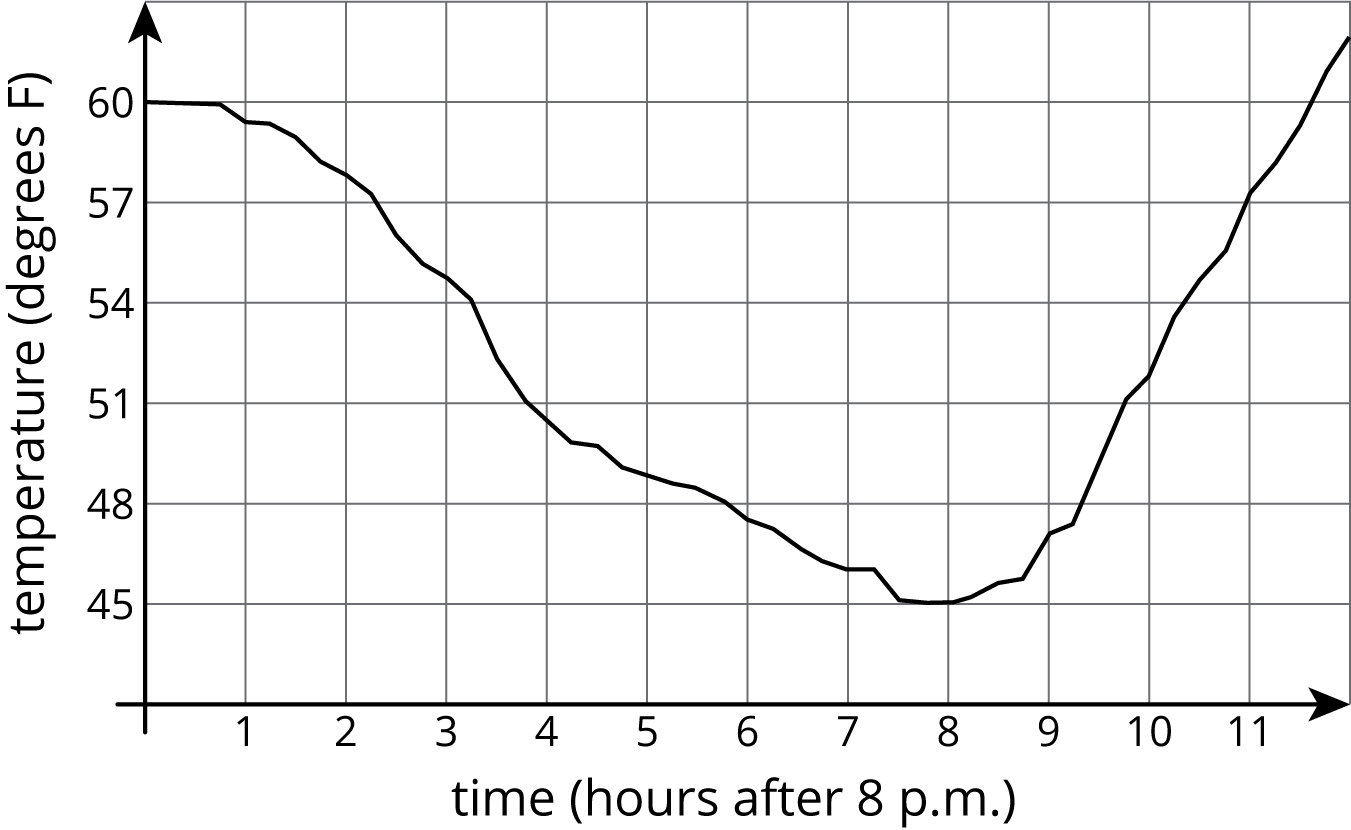
The graph of a function tells us what is happening in the context the function represents. In this example, the temperature starts out at \(60^\circ\) F at 8:00 p.m. It decreases during the night, reaching its lowest point at 8 hours after 8:00 p.m., or 4:00 a.m. Then it starts to increase again.
Glossary Entries
- dependent variable
A dependent variable represents the output of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of bananas is the dependent variable because it depends on the number of apples.
- independent variable
An independent variable represents the input of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy some apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of apples is the independent variable because we can choose any number for it.
- radius
A radius is a line segment that goes from the center to the edge of a circle. A radius can go in any direction. Every radius of the circle is the same length. We also use the word radius to mean the length of this segment.
For example, \(r\) is the radius of this circle with center \(O\).
