Lesson 6
Even More Graphs of Functions
Let’s draw a graph from a story.
6.1: Dog Run
Here are five pictures of a dog taken at equal intervals of time.

Diego and Lin drew different graphs to represent this situation:

They both used time as the independent variable. What do you think each one used for the dependent variable? Explain your reasoning.
6.2: Which Graph is It?
For each situation,
- name the independent and dependent variables
- pick the graph that best fits the situation, or sketch the graph if one isn't provided
- label the axes
- answer the question: which quantity is a function of which? Be prepared to explain your reasoning.
- Jada is training for a swimming race. The more she practices, the less time it takes for her to swim one lap.
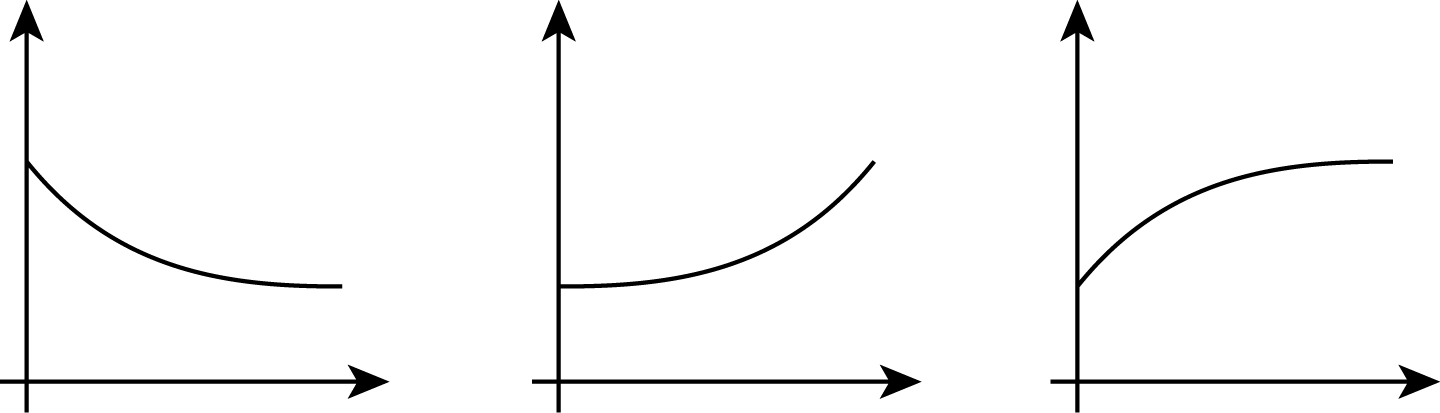
- Andre adds some money to a jar in his room each week for 3 weeks and then takes some out in week 4.
6.3: Sketching a Story about a Boy and a Bike
You will use the tools in the applet for creating a visual display that shows your response to each question.
Here is a story: “Noah was at home. He got on his bike and rode to his friend’s house and stayed there for awhile. Then he rode home again. Then he rode to the park. Then he rode home again.”
-
Sketch a graph of this story.
-
What are the two quantities? Label the axes with their names and units of measure. (For example, if this were a story about pouring water into a pitcher, one of your labels might say “volume (liters).”)
- Which quantity is a function of which? Explain your reasoning.
- Based on your graph, is his friend’s house or the park closer to Noah's home? Explain how you know.
- Read the story and all your responses again. Does everything make sense? If not, make changes to your work.
Note: To change the values on the axes, select the Move Graphics tool, click near the end of the axis you want to change, and drag it to grow or shrink it.

It is the year 3000. Noah’s descendants are still racing around the park, but thanks to incredible technological advances, now with much more powerful gadgets at their disposal. How might their newfound access to teleportation and time-travel devices alter the graph of stories of their daily adventures? Could they affect whether or not the distance from home is a function of the time elapsed?
Summary
Here is a graph showing Andre's distance as a function of time.
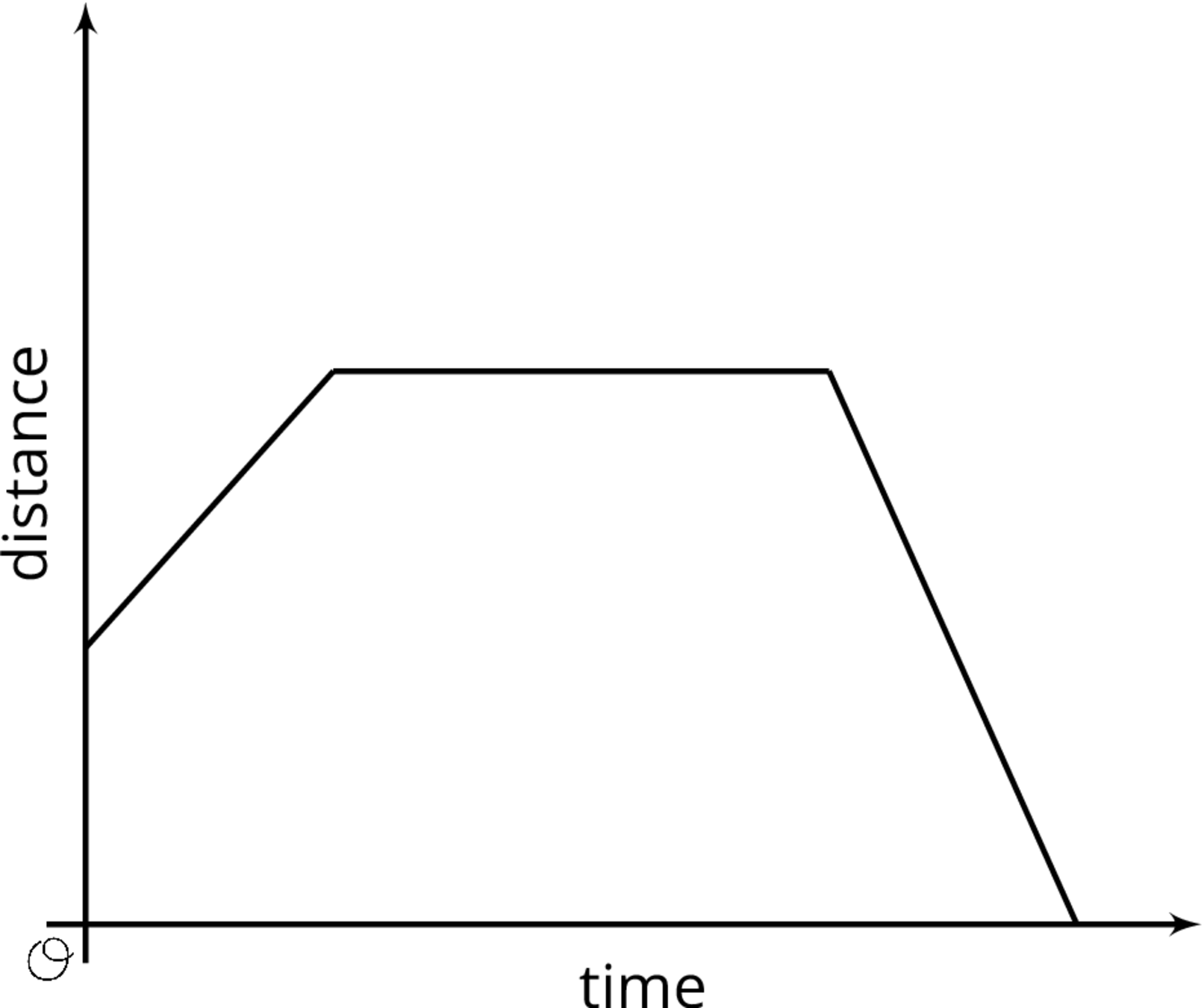
For a graph representing a context, it is important to specify the quantities represented on each axis. For example, if this is showing distance from home, then Andre starts at some distance from home (maybe at his friend’s house), moves further away (maybe to a park), then returns home. If instead the graph is showing distance from school, the story may be Andre starts out at home, moves further away (maybe to a friend's house), then goes to school. What could the story be if the graph is showing distance from a park?
Glossary Entries
- dependent variable
A dependent variable represents the output of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of bananas is the dependent variable because it depends on the number of apples.
- independent variable
An independent variable represents the input of a function.
For example, suppose we need to buy 20 pieces of fruit and decide to buy some apples and bananas. If we select the number of apples first, the equation \(b=20-a\) shows the number of bananas we can buy. The number of apples is the independent variable because we can choose any number for it.
- radius
A radius is a line segment that goes from the center to the edge of a circle. A radius can go in any direction. Every radius of the circle is the same length. We also use the word radius to mean the length of this segment.
For example, \(r\) is the radius of this circle with center \(O\).
