Lesson 16
Finding Cone Dimensions
Let’s figure out the dimensions of cones.
16.1: Number Talk: Thirds
For each equation, decide what value, if any, would make it true.
\(27=\frac13h\)
\(27=\frac13r^2\)
\(12\pi=\frac13\pi a\)
\(12\pi=\frac13\pi b^2\)
16.2: An Unknown Radius
The volume \(V\) of a cone with radius \(r\) is given by the formula \(V=\frac13 \pi r^2h\).
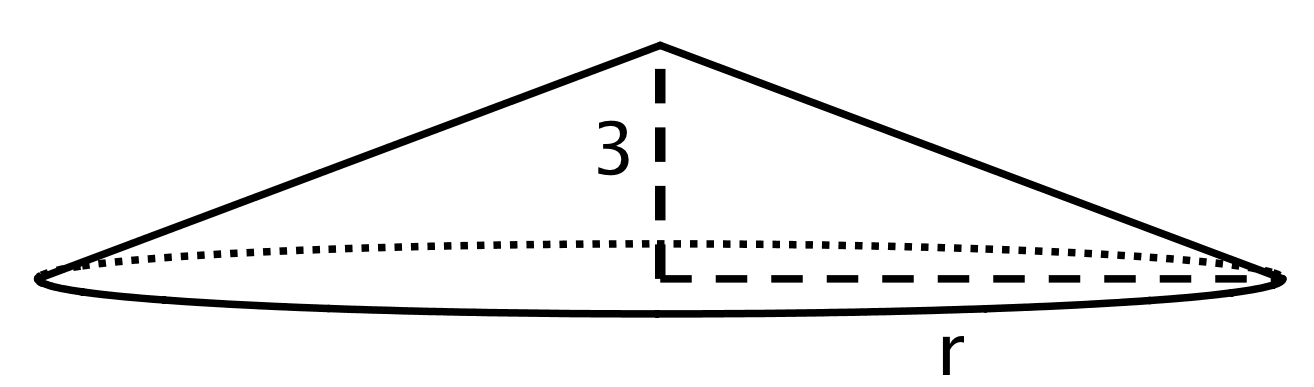
The volume of this cone with height 3 units and radius \(r\) is \(V=64\pi\) cubic units. This statement is true:
\(\displaystyle 64\pi =\frac13 \pi r^2 \boldcdot 3\) What does the radius of this cone have to be? Explain how you know.
16.3: Cones with Unknown Dimensions
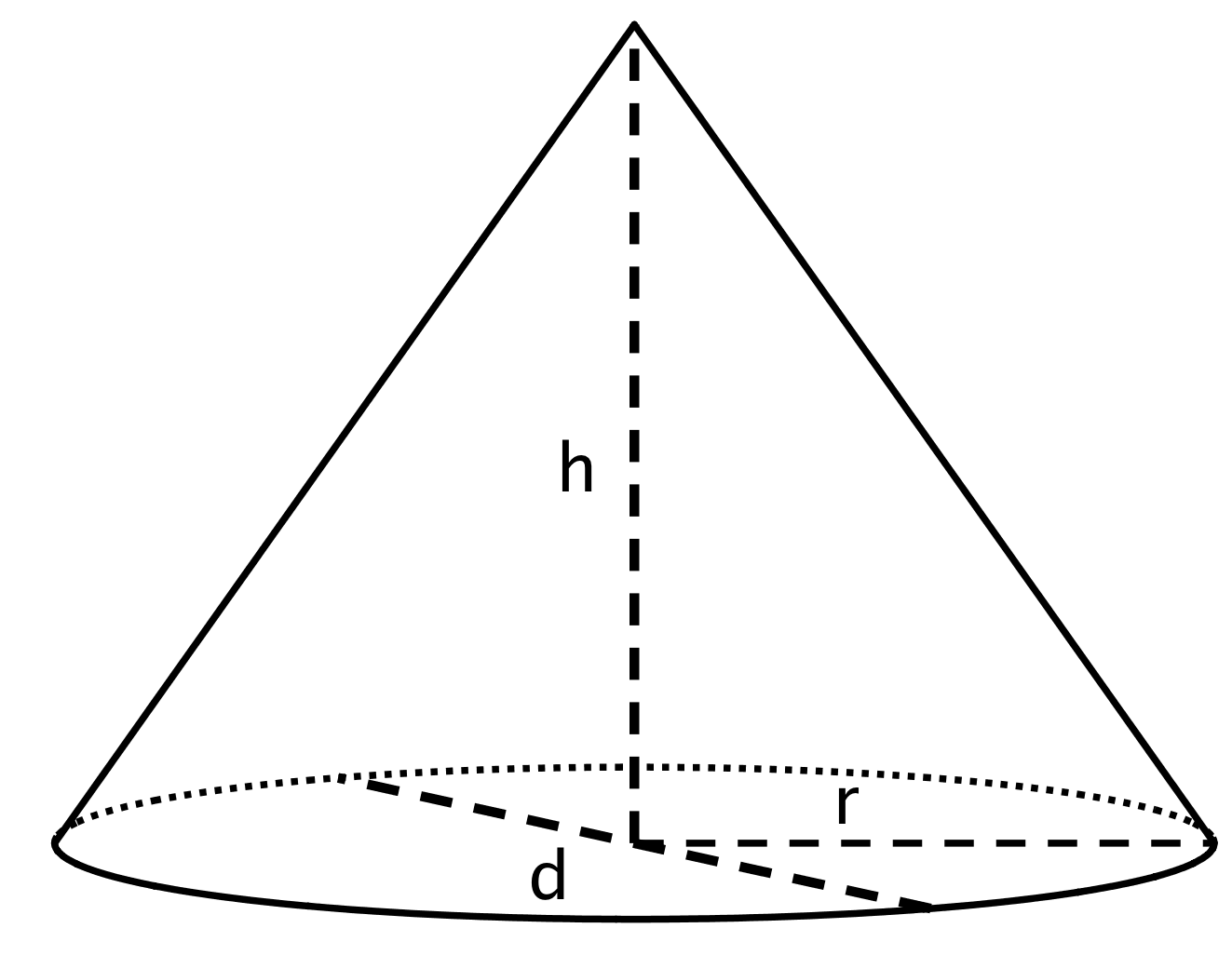
Each row of the table has some information about a particular cone. Complete the table with the missing dimensions.
| diameter (units) | radius (units) | area of the base (square units) | height (units) | volume of cone (cubic units) |
|---|---|---|---|---|
| 4 | 3 | |||
| \(\frac{1}{3}\) | 6 | |||
| \(144\pi\) | \(\frac14\) | |||
| 20 | \(200\pi\) | |||
| 12 | \(64\pi\) | |||
| 3 | 3.14 |
A frustum is the result of taking a cone and slicing off a smaller cone using a cut parallel to the base.
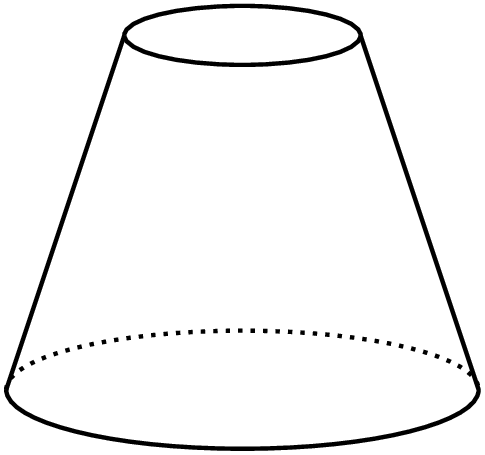
Find a formula for the volume of a frustum, including deciding which quantities you are going to include in your formula.
16.4: Popcorn Deals
A movie theater offers two containers:

Which container is the better value? Use 3.14 as an approximation for \(\pi\).
Summary
As we saw with cylinders, the volume \(V\) of a cone depends on the radius \(r\) of the base and the height \(h\):
\(\displaystyle V=\frac13 \pi r^2h\)
If we know the radius and height, we can find the volume. If we know the volume and one of the dimensions (either radius or height), we can find the other dimension.
For example, imagine a cone with a volume of \(64\pi\) cm3, a height of 3 cm, and an unknown radius \(r\). From the volume formula, we know that
\(\displaystyle 64 \pi = \frac{1}{3}\pi r^2 \boldcdot 3\)
Looking at the structure of the equation, we can see that \(r^2 = 64\), so the radius must be 8 cm.
Now imagine a different cone with a volume of \(18 \pi\) cm3, a radius of 3 cm, and an unknown height \(h\). Using the formula for the volume of the cone, we know that
\(\displaystyle 18 \pi = \frac{1}{3} \pi 3^2h\)
so the height must be 6 cm. Can you see why?
Video Summary
Glossary Entries
- cone
A cone is a three-dimensional figure like a pyramid, but the base is a circle.
- cylinder
A cylinder is a three-dimensional figure like a prism, but with bases that are circles.
- sphere
A sphere is a three-dimensional figure in which all cross-sections in every direction are circles.