Lesson 18
Scaling Two Dimensions
Let’s change more dimensions of shapes.
Problem 1
There are many cylinders with a height of 18 meters. Let \(r\) represent the radius in meters and \(V\) represent the volume in cubic meters.
-
Write an equation that represents the volume \(V\) as a function of the radius \(r\).
-
Complete this table, giving three possible examples.
\(r\) \(V\) 1 -
If the radius of a cylinder is doubled, does the volume double? Explain how you know.
-
Is the graph of this function a line? Explain how you know.
Problem 2
As part of a competition, Diego must spin around in a circle 6 times and then run to a tree. The time he spends on each spin is represented by \(s\) and the time he spends running is \(r\). He gets to the tree 21 seconds after he starts spinning.
- Write an equation showing the relationship between \(s\) and \(r\).
- Rearrange the equation so that it shows \(r\) as a function of \(s\).
- If it takes Diego 1.2 seconds to spin around each time, how many seconds did he spend running?
Problem 3
The table and graph represent two functions. Use the table and graph to answer the questions.
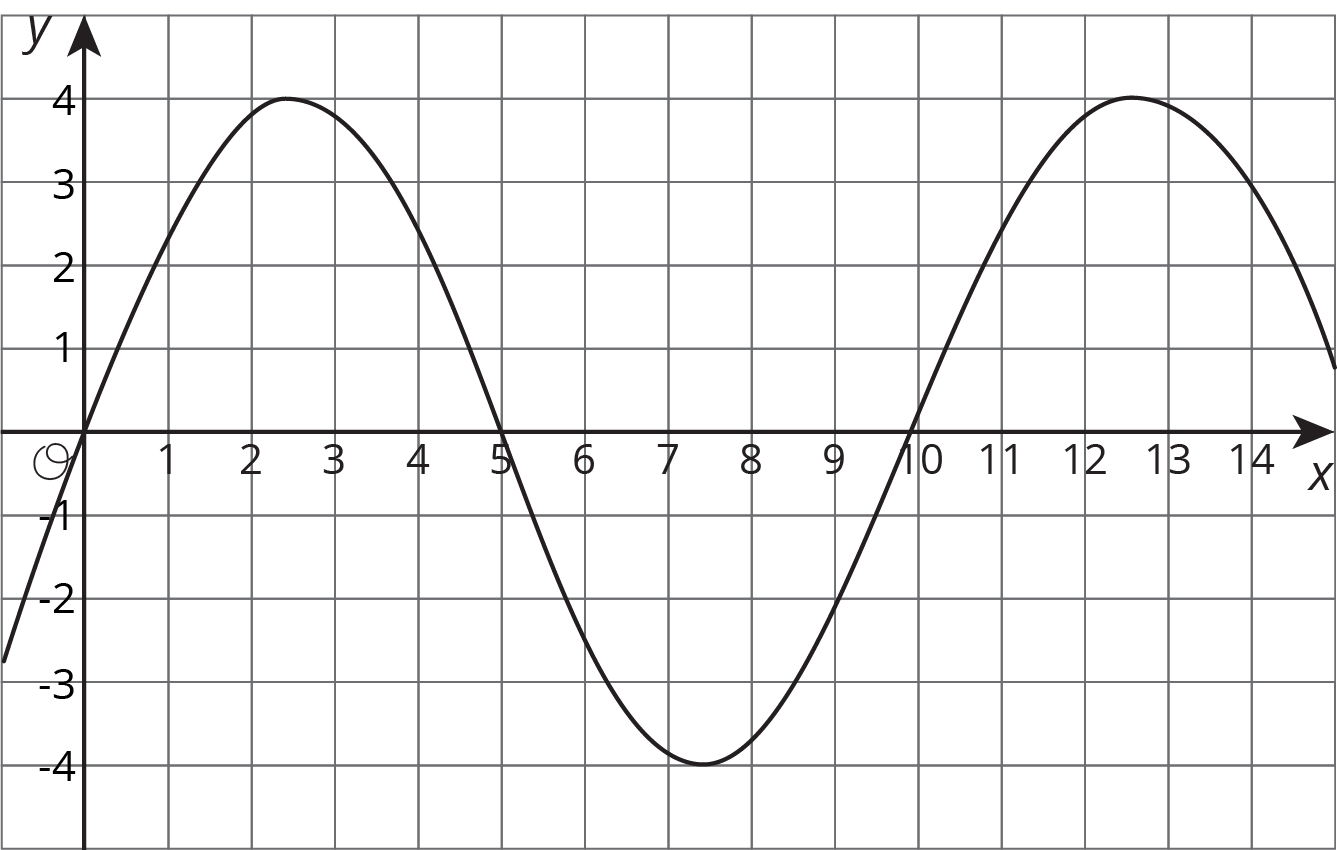
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| \(y\) | 3 | -1 | 0 | 4 | 5 | -1 |
- For which values of \(x\) is the output from the table less than the output from the graph?
- In the graphed function, which values of \(x\) give an output of 0?
Problem 4
A cone has a radius of 3 units and a height of 4 units.
-
What is this volume of this cone?
-
Another cone has quadruple the radius, and the same height. How many times larger is the new cone’s volume?