Lesson 16
Finding Cone Dimensions
Let’s figure out the dimensions of cones.
Problem 1
The volume of this cylinder is \(175\pi\) cubic units.
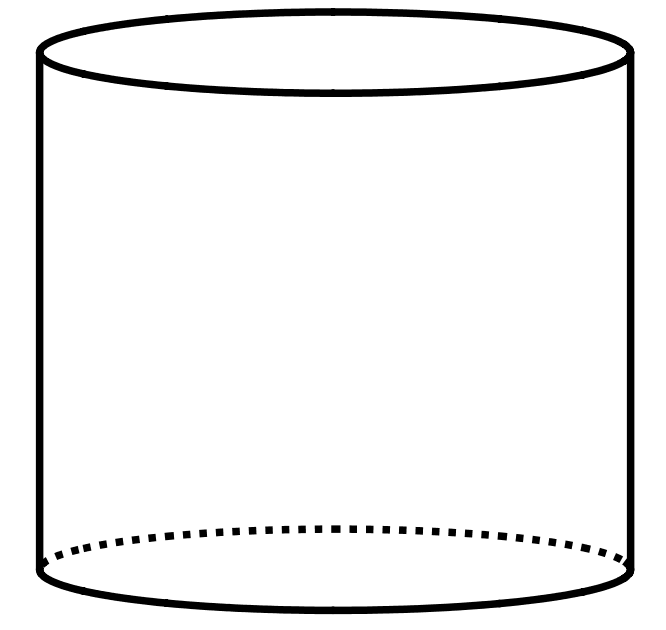
What is the volume of a cone that has the same base area and the same height?
Problem 2
A cone has volume \(12\pi\) cubic inches. Its height is 4 inches. What is its radius?
Problem 3
A cone has volume \(3 \pi\).
-
If the cone’s radius is 1, what is its height?
-
If the cone’s radius is 2, what is its height?
-
If the cone’s radius is 5, what is its height?
-
If the cone’s radius is \(\frac 1 2\), what is its height?
-
If the cone's radius in \(r\), then what is the height?
Problem 4
Three people are playing near the water. Person A stands on the dock. Person B starts at the top of a pole and ziplines into the water, then climbs out of the water. Person C climbs out of the water and up the zipline pole. Match the people to the graphs where the horizontal axis represents time in seconds and the vertical axis represents height above the water level in feet.

Problem 5
A room is 15 feet tall. An architect wants to include a window that is 6 feet tall. The distance between the floor and the bottom of the window is \(b\) feet. The distance between the ceiling and the top of the window is \(a\) feet. This relationship can be described by the equation \(\displaystyle a = 15 - (b + 6)\)
- Which variable is independent based on the equation given?
- If the architect wants \(b\) to be 3, what does this mean? What value of \(a\) would work with the given value for \(b\)?
- The customer wants the window to have 5 feet of space above it. Is the customer describing \(a\) or \(b\)? What is the value of the other variable?