Lesson 8

Linear Functions

View Student Lesson

Problem 1

Two cars drive on the same highway in the same direction. The graphs show the distance, \(d\), of each one as a function of time, \(t\). Which car drives faster? Explain how you know.

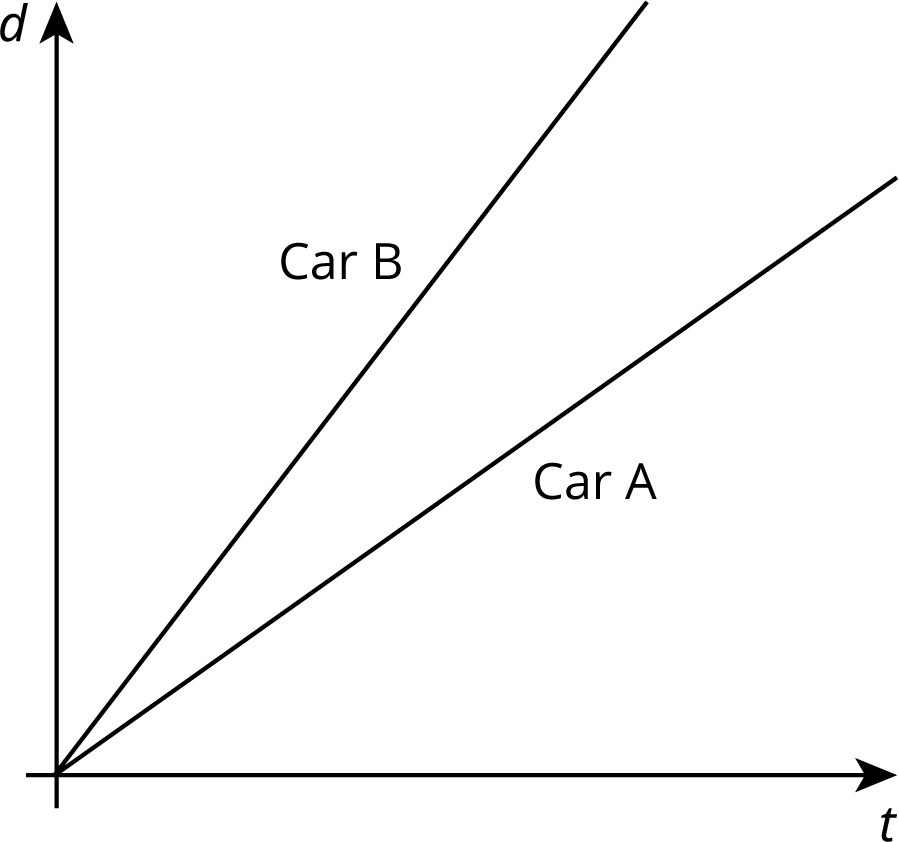
Set of axes, horizontal, t, vertical d. Two lines labeled Car A and Car B both begin at the origin and climb as they go right, Car B climbs at a steeper angle.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Two car services offer to pick you up and take you to your destination. Service A charges 40 cents to pick you up and 30 cents for each mile of your trip. Service B charges $1.10 to pick you up and charges \(c\) cents for each mile of your trip.

  1. Match the services to the Lines \(\ell\) and \(m\).
  2. For Service B, is the additional
    charge per mile greater or less than
    30 cents per mile of the trip?
    Explain your reasoning.
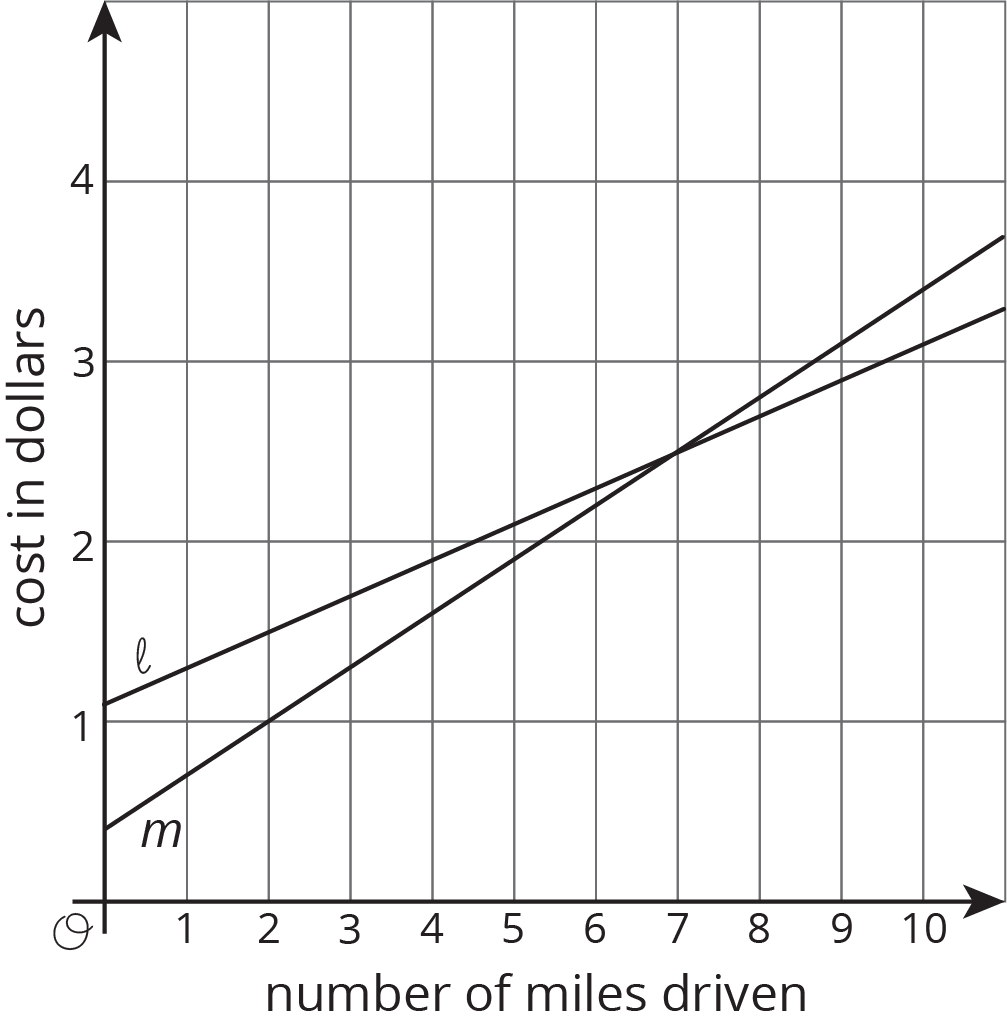
Coordinate plane, horizontal, miles driven, 0 to 10, vertical, cost, dollars, 0 to 4. Line l through 0 comma 1 point 1, & 7 comma 2 point 5. Line m through 0 comma point 5, & 7 comma point 5.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Kiran and Clare like to race each other home from school. They run at the same speed, but Kiran's house is slightly closer to school than Clare's house. On a graph, their distance from their homes in meters is a function of the time from when they begin the race in seconds.

  1. As you read the graphs left to right, would the lines go up or down?
  2. What is different about the lines representing Kiran's run and Clare's run?
  3. What is the same about the lines representing Kiran's run and Clare's run?

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Write an equation for each line.

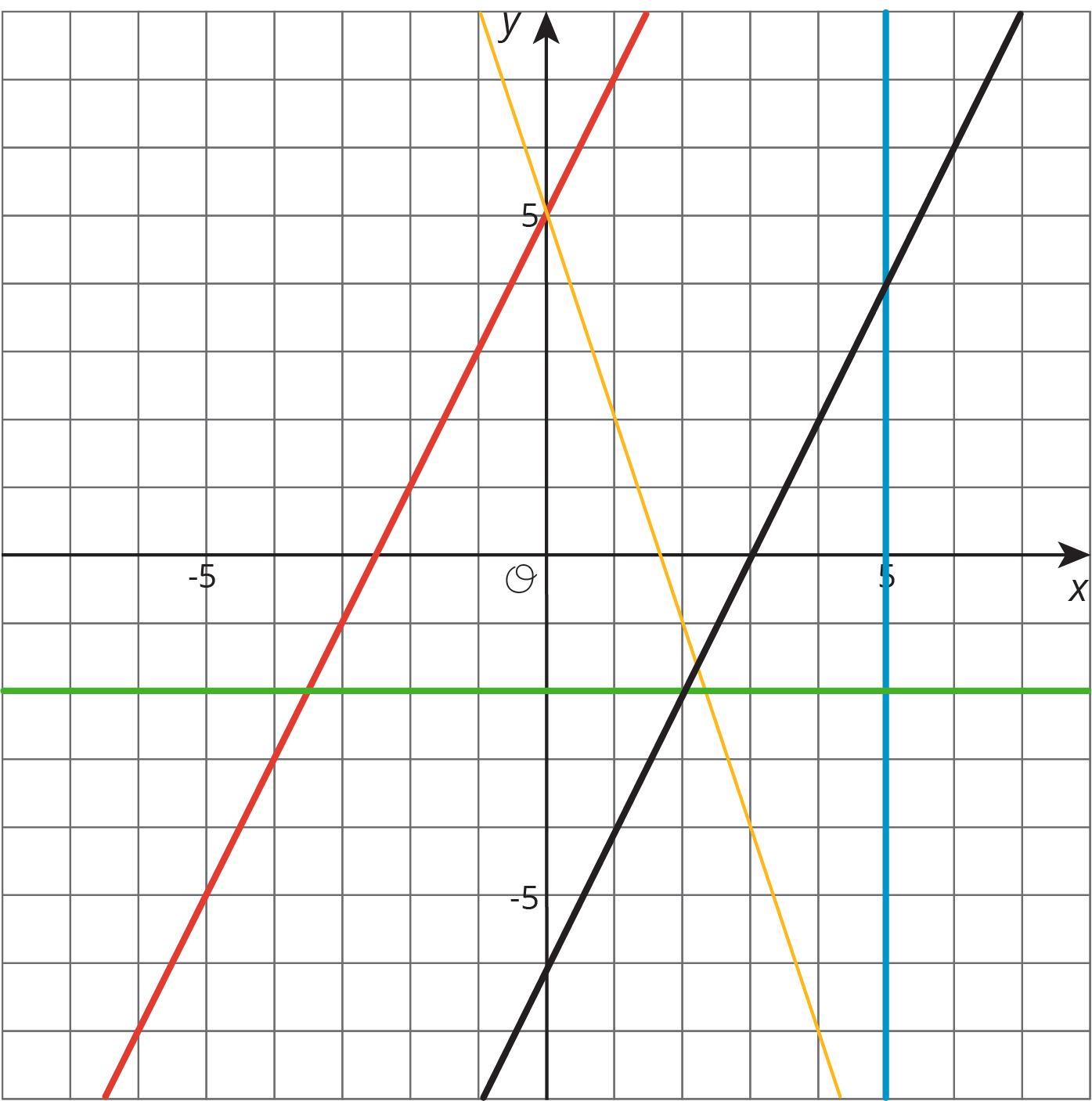
Five lines.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 11.)