Lesson 11

Filling Containers

View Student Lesson

Problem 1

Cylinder A, B, and C have the same radius but different heights. Put the cylinders in order of their volume from least to greatest.

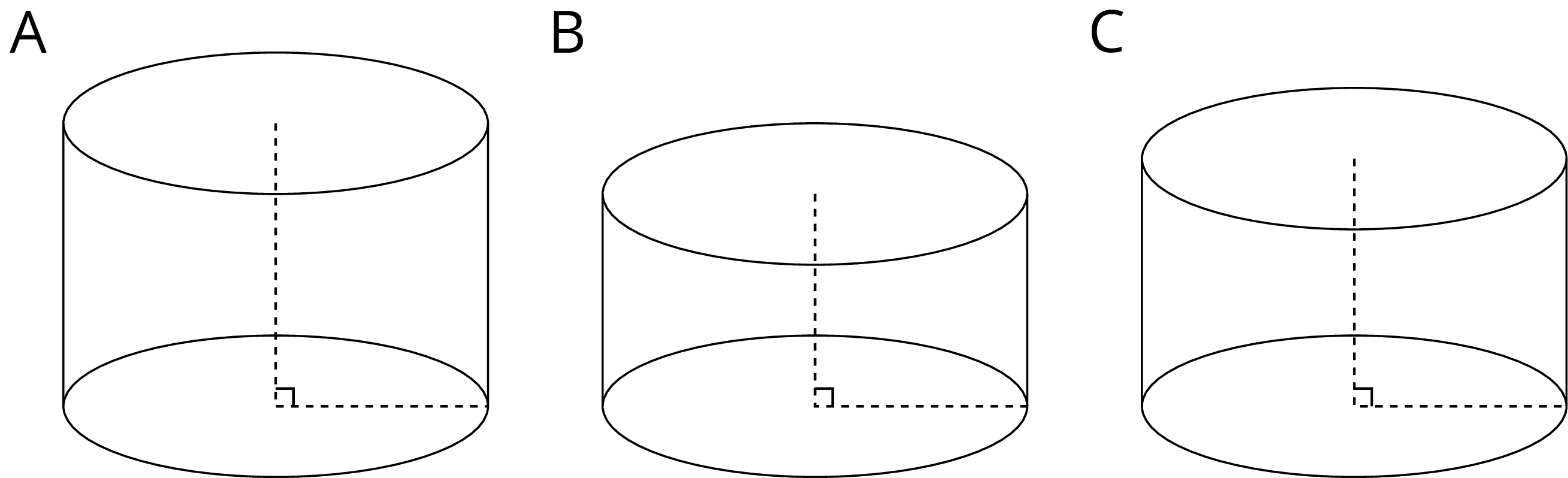
Three cylinders, A, B and C. No dimensions are given. Cylinder A is taller than Cylinder B. Cylinder C is taller than Cylinder B, and not as tall as Cylinder A

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Two cylinders, \(a\) and \(b\), each started with different amounts of water. The graph shows how the height of the water changed as the volume of water increased in each cylinder. Match the graphs of \(a\) and \(b\) to Cylinders P and Q. Explain your reasoning.

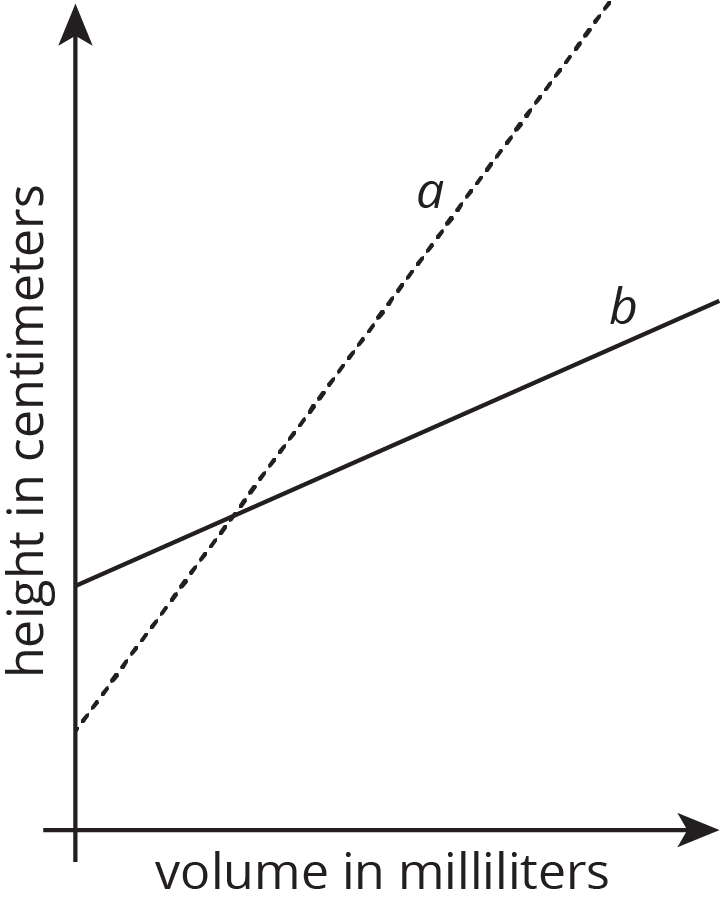
Graph, two lines. Horizontal axis, volume in milliliters, vertical, height in centimeters. Line a, positive slope. Line b, greater y-intercept than line a, but the slope is not as steep.
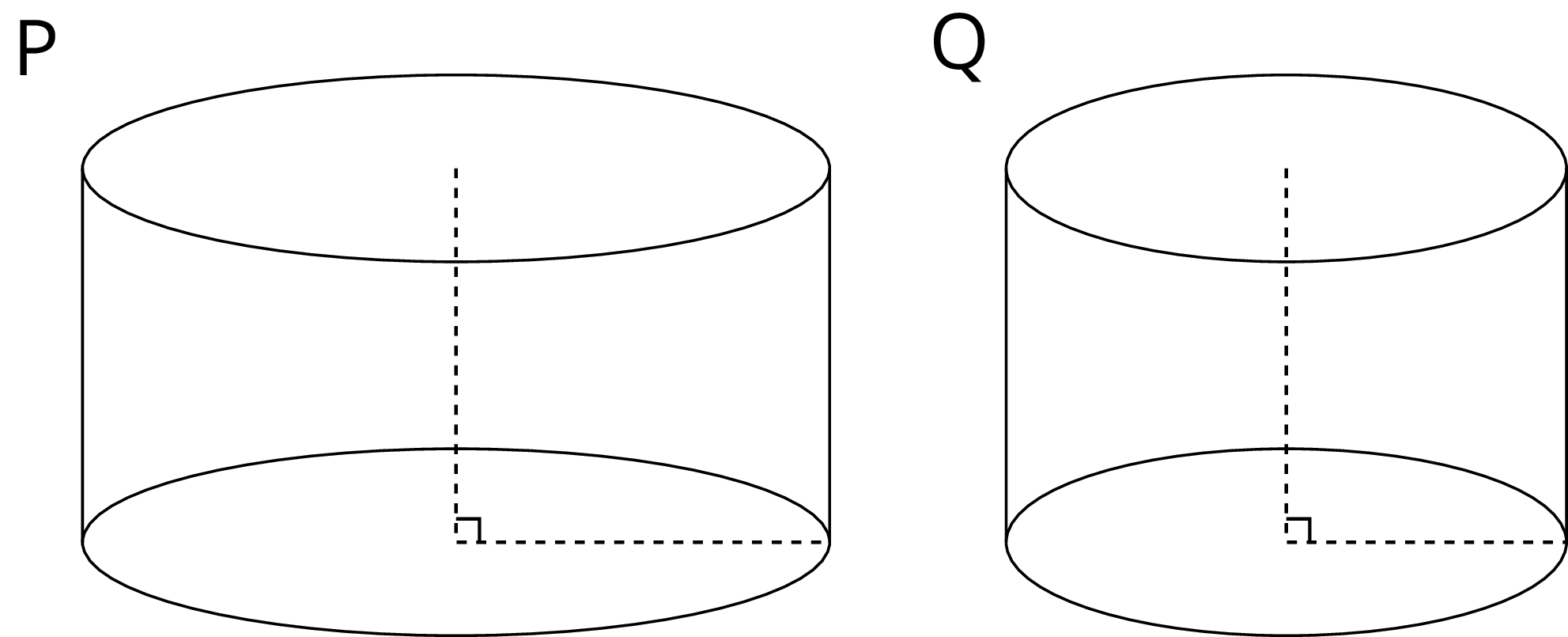
Two cylinders, P and Q. No dimensions are marked. The cylinders appear to have the same height, but Cylinder P is wider than Cylinder Q.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Which of the following graphs could represent the volume of water in a cylinder as a function of its height? Explain your reasoning.

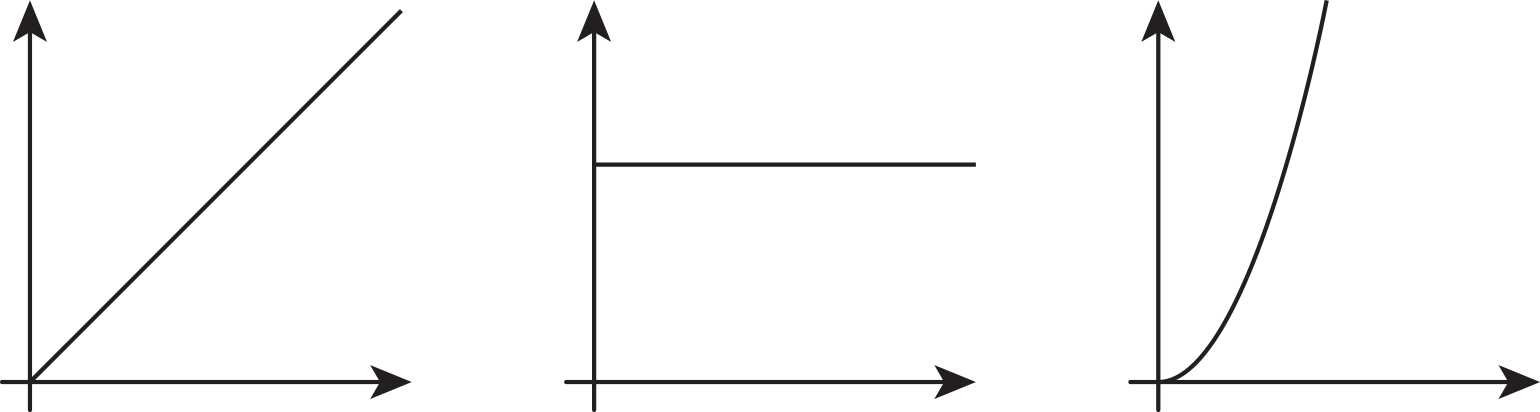
Three graphs, all quadrant 1.  First, straight line, through origin, positive slope. Second, horizontal line begins above origin. Third, curve begins at origin, increases as it moves right.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Together, the areas of the rectangles sum to 30 square centimeters.

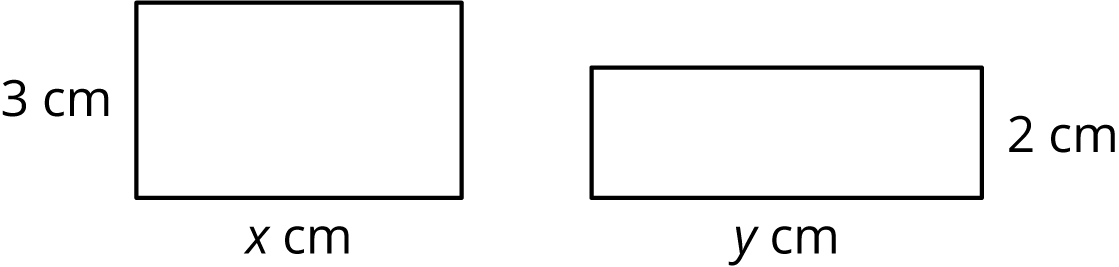
Two rectangles. First, 3 centimeters by x centimeters. Second, y centimeters by 2 centimeters.
  1. Write an equation showing the relationship between \(x\) and \(y\).
  2. Fill in the table with the missing values.
    \(x\) 3 8 12
    \(y\) 5 10

Solution

For access, consult one of our IM Certified Partners.

(From Unit 5, Lesson 3.)