Lesson 3

Adding and Subtracting Decimals with Few Non-Zero Digits

View Student Lesson

Problem 1

Here is a base-ten diagram that represents 1.13. Use the diagram to find \(1.13 - 0.46\).

Explain or show your reasoning.

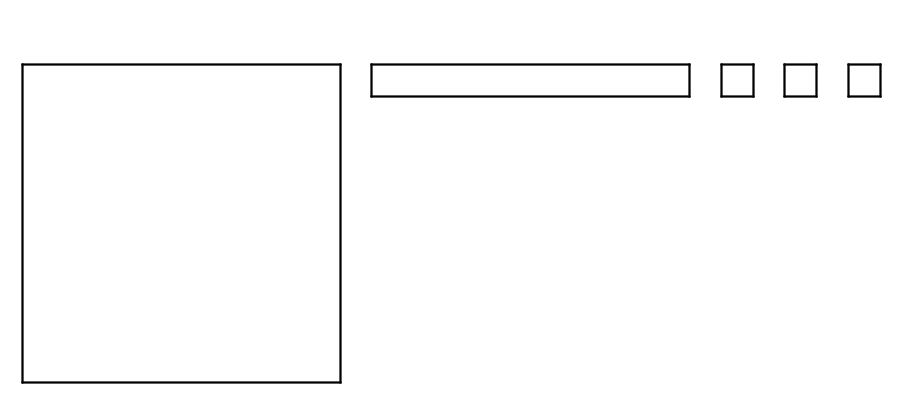
A base-ten diagram representing 1 point 1 3. 1 large square, 1 rectangle, and 3 small squares. 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Compute the following sums. If you get stuck, consider drawing base-ten diagrams.

  1. \(0.027 + 0.004\)

  2. \(0.203 + 0.01\)

  3. \(1.2 + 0.145\)

Solution

For access, consult one of our IM Certified Partners.

Problem 3

A student said we cannot subtract 1.97 from 20 because 1.97 has two decimal digits and 20 has none. Do you agree with him? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Decide which calculation shows the correct way to find \(0.3-0.006\) and explain your reasoning.

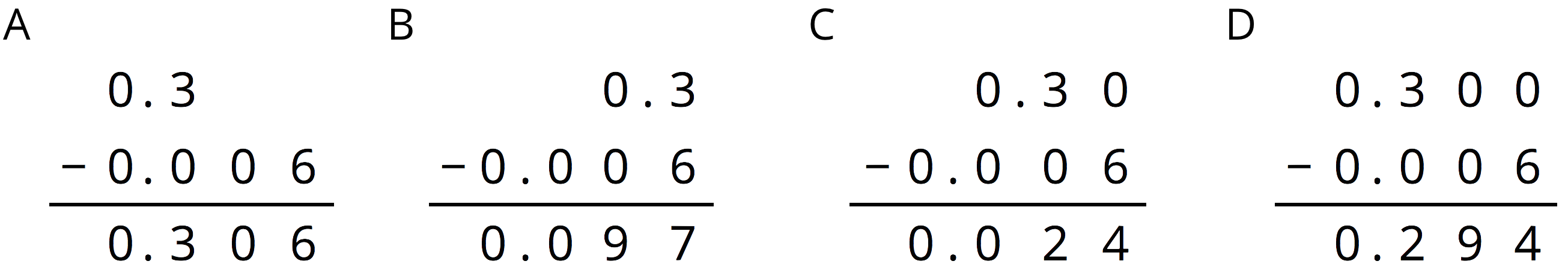
4 subtraction problems.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Complete the calculations so that each shows the correct difference.

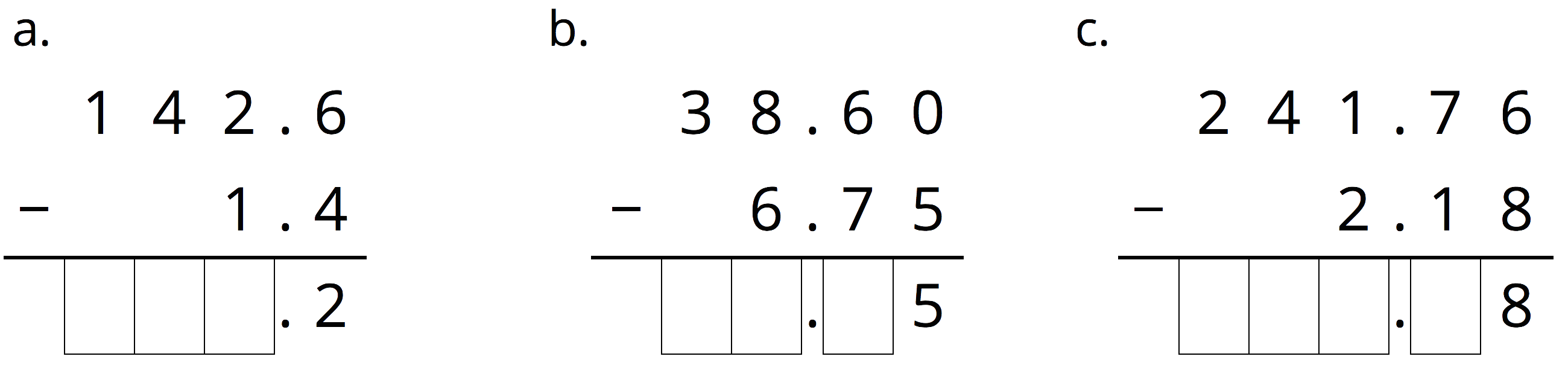
3 decimal subtraction problems. 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 6

The school store sells pencils for $0.30 each, hats for $14.50 each, and binders for $3.20 each. Elena would like to buy 3 pencils, a hat, and 2 binders. She estimated that the cost will be less than $20.

  1. Do you agree with her estimate? Explain your reasoning.
  2. Estimate the number of pencils could she buy with $5. Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 5, Lesson 1.)

Problem 7

A rectangular prism measures \(7\frac{1}{2}\) cm by 12 cm by \(15\frac{1}{2}\) cm.

  1. Calculate the number of cubes with edge length \(\frac{1}{2}\) cm that fit in this prism.
  2. What is the volume of the prism in \(\text{cm}^3\)? Show your reasoning. If you are stuck, think about how many cubes with \(\frac12\)-cm edge lengths fit into \(1\text{ cm}^3\).

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 15.)

Problem 8

At a constant speed, a car travels 75 miles in 60 minutes. How far does the car travel in 18 minutes? If you get stuck, consider using the table.

minutes distance in miles
60 75
6
18

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 12.)