Lesson 3

Adding and Subtracting Decimals with Few Non-Zero Digits

Let’s add and subtract decimals.

3.1: Do the Zeros Matter?

  1. Evaluate mentally: 1.009+0.391

  2. Decide if each equation is true or false. Be prepared to explain your reasoning.

    1. 34.56000 = 34.56
    2. 25 = 25.0
    3. 2.405 = 2.45

3.2: Calculating Sums

  1. Andre and Jada drew base-ten diagrams to represent 0.007 + 0.004. Andre drew 11 small rectangles. Jada drew only two figures: a square and a small rectangle.

    Two base-ten diagrams, Andre and Jada. Andre, 11 small rectangles. Jada, 1 square and 1 small rectangle.
    1. If both students represented the sum correctly, what value does each small rectangle represent? What value does each square represent?
    2. Draw or describe a diagram that could represent the sum 0.008 + 0.07.

  2. Here are two calculations of 0.2 + 0.05. Which is correct? Explain why one is correct and the other is incorrect.

    Two calculations of zero point 2 plus zero point zero five are indicated. 
  3. Compute each sum. If you get stuck, consider drawing base-ten diagrams to help you.
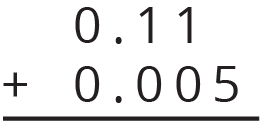
    1. The vertical calculation of zero point 1 1 plus zero point zero zero 5 is indicated by aligning the ones units, tenths units, hundredths units, and thousandths units.
    2. 0.209 + 0.01
    3. 10.2 + 1.1456
  • The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
  • Select a Block tool, and then click on the screen to place it.
  • Click on the Move tool (the arrow) when you are done choosing blocks.
  • Subtract by deleting with the delete tool (the trash can), not by crossing out.

3.3: Subtracting Decimals of Different Lengths

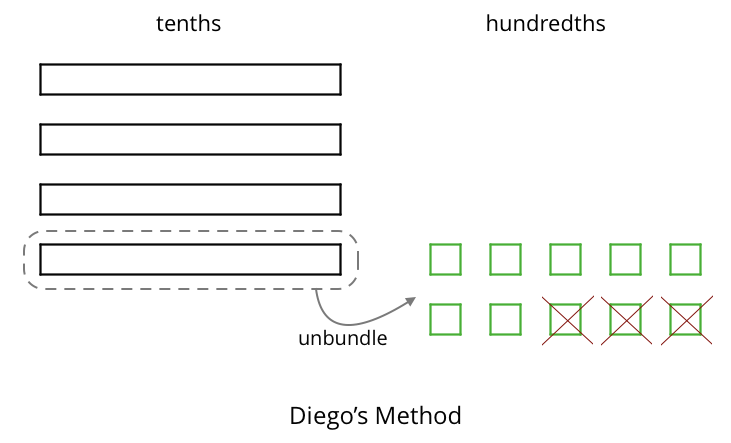
To represent 0.4 - 0.03, Diego and Noah drew different diagrams. Each rectangle represented 0.1. Each square represented 0.01.

  • Diego started by drawing 4 rectangles to represent 0.4. He then replaced 1 rectangle with 10 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 3 rectangles and 7 squares in his diagram.

    A base-ten diagram labeled “Diego’s Method.” 

  • Noah started by drawing 4 rectangles to represent 0.4. He then crossed out 3 of rectangles to represent the subtraction, leaving 1 rectangle in his diagram.

    Noah's Method. tenths. 4 tenth pieces. 3 crossed out.

  1. Do you agree that either diagram correctly represents 0.4 - 0.03? Discuss your reasoning with a partner.

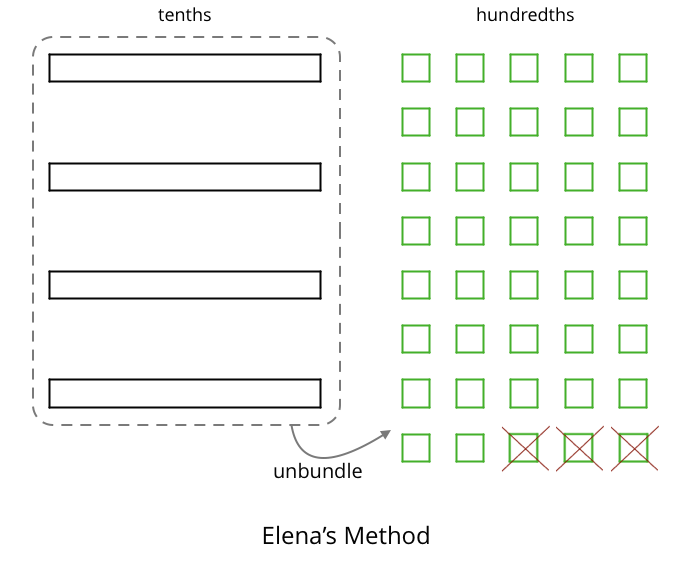
  2. To represent 0.4 - 0.03, Elena drew another diagram. She also started by drawing 4 rectangles. She then replaced all 4 rectangles with 40 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 37 squares in her diagram. Is her diagram correct? Discuss your reasoning with a partner.

    A base-ten diagram labeled “Elena's Method.” 
  3. Find each difference. If you get stuck, you can use the applet to represent each expression and find its value.
    1. 0.3 - 0.05
    2. 2.1 - 0.4
    3. 1.03 - 0.06
    4. 0.02 - 0.007

Be prepared to explain your reasoning.

  • The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
  • Select a Block tool, and then click on the screen to place it.
  • Click on the Move tool (the arrow) when you are done choosing blocks.
  • Subtract by deleting with the delete tool (the trash can), not by crossing out.



A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.

At the Auld Shoppe, a shopper buys items that are worth 2 yellow jewels, 2 green jewels, 2 blue jewels, and 1 indigo jewel. If they came into the store with 1 red jewel, 1 yellow jewel, 2 green jewels, 1 blue jewel, and 2 violet jewels, what jewels do they leave with? Assume the shopkeeper gives them their change using as few jewels as possible. 

Summary

Base-ten diagrams can help us understand subtraction as well. Suppose we are finding 0.23 - 0.07. Here is a diagram showing 0.23, or 2 tenths and 3 hundredths. 

Base ten diagram. 0 point 23. Two rectangles in the tenths column. 3 small squares in the hundredths column.

Subtracting 7 hundredths means removing 7 small squares, but we do not have enough to remove. Because 1 tenth is equal to 10 hundredths, we can “unbundle” (or decompose) one of the tenths (1 rectangle) into 10 hundredths (10 small squares).

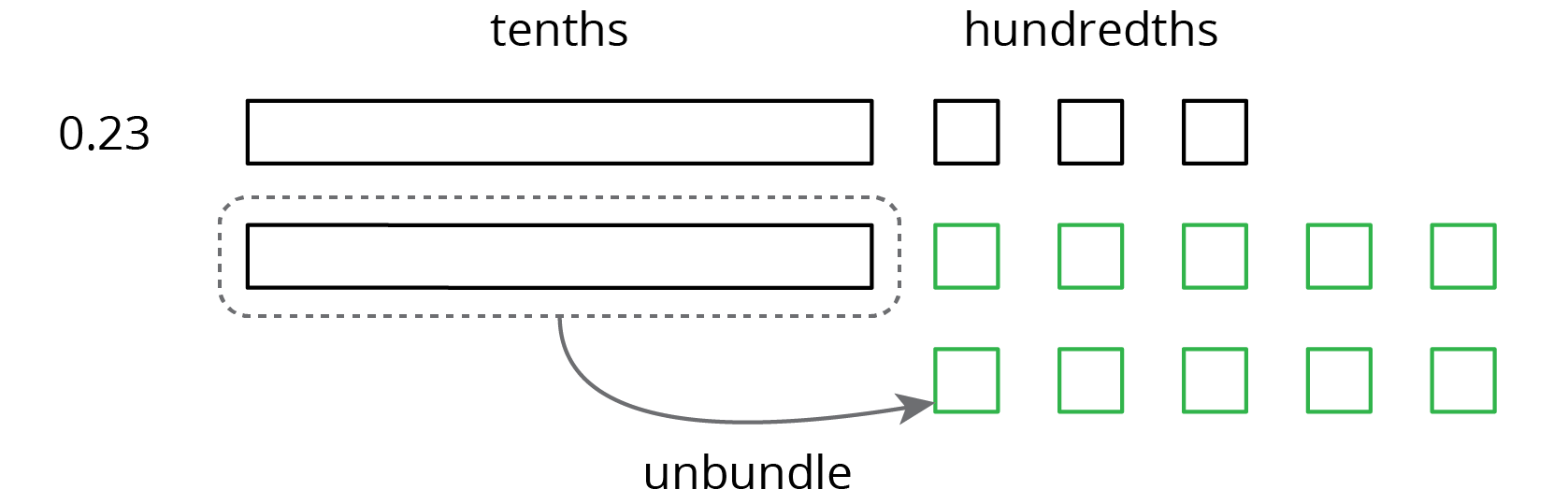
Base ten diagram. 

We now have 1 tenth and 13 hundredths, from which we can remove 7 hundredths.

Base ten diagram. 

We have 1 tenth and 6 hundredths remaining, so 0.23 - 0.07 = 0.16.

Base ten diagram. 0 point 16. One rectangle in the tenths column. 6 small squares in the hundredths column.

Here is a vertical calculation of 0.23 - 0.07.

Vertical subtraction. 

Notice how this representation also shows a tenth is unbundled (or decomposed) into 10 hundredths in order to subtract 7 hundredths.


This works for any decimal place. Suppose we are finding 0.023 - 0.007. Here is a diagram showing 0.023.

Base 10 diagram. 0 point 0 2 3. Two small squares in the hundredths column. Three small rectangles in the thousandths column.

We want to remove 7 thousandths (7 small rectangles). We can “unbundle” (or decompose) one of the hundredths into 10 thousandths.

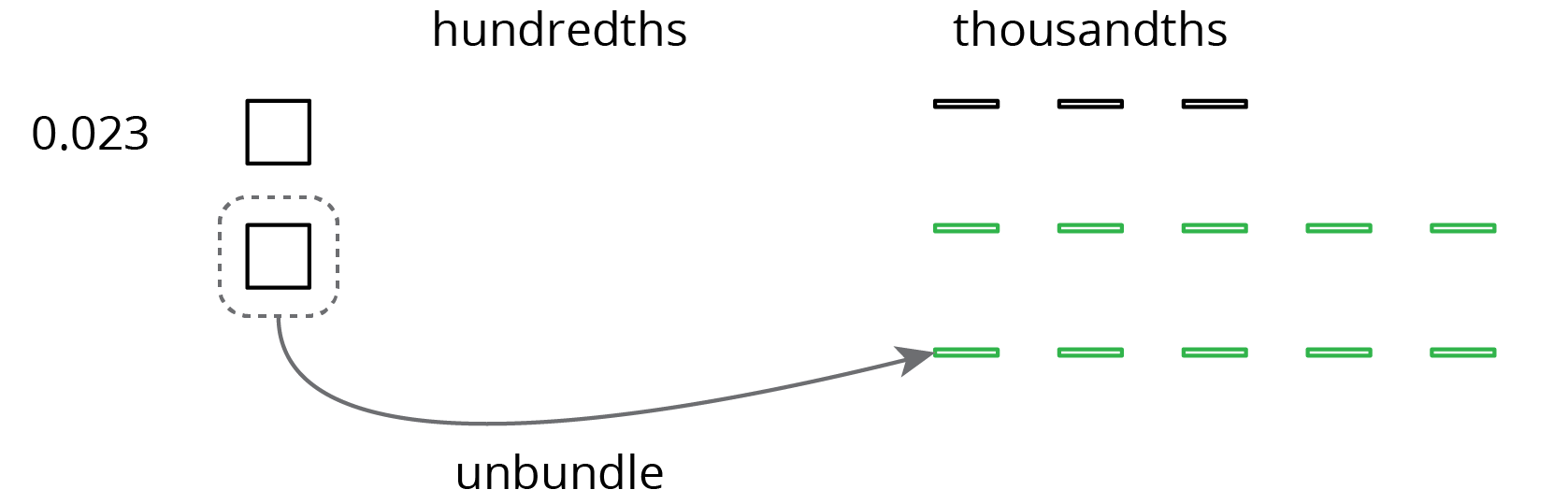
Base 10 diagram. 

Now we can remove 7 thousandths.

Base 10 diagram. 

We have 1 hundredth and 6 thousandths remaining, so 0.023 - 0.007 = 0.016.

Base ten diagram. 0 point 0 1 6. One small square in the hundredths column. 6 small rectangles in the thousandths column.

Here is a vertical calculation of 0.023 - 0.007.

Vertical subtraction.