Lesson 4
Adding and Subtracting Decimals with Many Non-Zero Digits
4.1: The Cost of a Photo Print (5 minutes)
Warm-up
This warm-up prompts students to review the placement of the digits when subtracting decimal numbers using an efficient algorithm. The first question gives students a chance to think about how different placements of the 5 (the first number) affects the subtraction and the difference. It also gives insight to how students interpret the 5 and its value. For examples:
- Would they place the decimal point directly after the 5?
- When placing 5 above 7 (in the tenths place), do they see it as 5 ones or as 5 tenths?
- Do they wonder if the 5 is missing a decimal point in the second and third case?
In the second and third questions, a context is introduced for the same subtraction. Notice how students interpret the problem now; the equivalence of 5 and 5.00 should become much more apparent in a money context. Identify a couple of students who have correct responses so they could share later.
Launch
Give students up to 1 minute to think about the first question and then ask them to share what they noticed and wondered. Then, give students 1 minute of quiet work time for the remaining questions and follow with a whole-class discussion.
Student Facing
-
Here are three ways to write a subtraction calculation. What do you notice? What do you wonder?
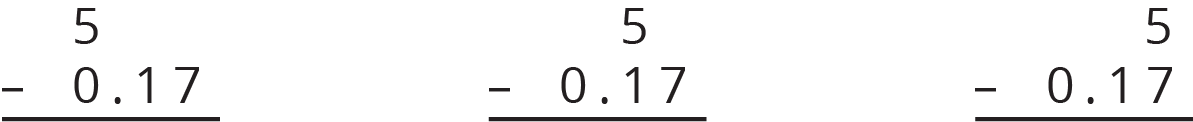
-
Clare bought a photo for 17 cents and paid with a $5 bill. Look at the previous question. Which way of writing the numbers could Clare use to find the change she should receive? Be prepared to explain how you know.
-
Find the amount of change that Clare should receive. Show your reasoning, and be prepared to explain how you calculate the difference of 0.17 and 5.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask a few students to share which way they think Clare could write the calculation (in the second question) in order to find the amount of change. In this particular case, the first setup is the most conducive to correct computation, but there is not one correct answer. Students could find the answer with any one of the setups as long as they understand that the 5 represents $5.00. If any students choose the second or third setup because they can mentally subtract the values without lining them up by place values, invite them to share their reasoning. Ask if they would use the same strategy for dealing with longer decimals (e.g., \(5.23 - 0.4879\)) and, if not, what approach might be more conducive to correct calculation in those cases.
Encourage more students to be involved in the conversation by asking questions such as:
- “Do you agree or disagree? Why?”
- “Can anyone explain ___’s reasoning in their own words?”
- “What is important for us to think about when subtracting this way?”
- “How could we have solved this problem mentally?”
4.2: Decimals All Around (15 minutes)
Activity
This activity has two parts and serves two purposes. The first two problems aim to help students see the limits of using base-ten diagrams to add and subtract numbers and to think about choosing more efficient methods. The latter three questions prompt students to reason about addition and subtraction of numbers with more decimal places in the context of situations. Students need to determine the appropriate operations for the given situations, perform the calculations, and then relate their answers back to the contexts (MP2).
As students work, check that they remember to line up the decimal points, write zeros when needed, and label their answers with units of measurement (for the last three questions). Identify one student to present each question. For the last question, there are two likely methods for solving (as outlined in the solutions). If both methods arise, they should both be presented.
Launch
Ask students to read the first 2 problems and think about which method of reasoning might work best. Give students 5 minutes of quiet time to work on these problems. Observe which methods students choose and check their work for accuracy.
Afterwards, take a few minutes to discuss their answers and methods. Ask one or more of the following questions before moving onto the second half of the activity:
- “Would base-ten diagrams work well for \(318.8 - 94.63\)? Why or why not?” (No, it is time consuming to draw and keep track of so many pieces. Yes, I can draw 3 large squares for 300, 1 rectangle for 10, 8 small squares for 8, etc., remove pieces in the amount of 94.63, and count what is left.)
- “What challenges did you face in computing \(0.02 - 0.0116\) using a diagram?” (I needed to take away 116 ten-thousandths from 2 hundredths, so I had to exchange hundredths with ten-thousandths, which meant drawing or showing many smaller pieces.) “What about using vertical calculations?” (The first number is two digits shorter than the second, which meant some extra steps.)
- “When might base-ten diagrams be a good choice for finding a difference (or sum)?” (When the numbers are simple or short so the diagrams do not take too long to draw.)
- “When might an algorithm be a good choice for finding a difference (or sum)?” (For a difference like \(6.739258 - 0.8536672\), it will be time consuming to draw pictures and label each place value. The algorithm takes some time as well but is more efficient than drawing pictures.)
After this discussion, have students work independently on the remaining problems. During this time, monitor and select individuals to share their work during the whole-class discussion.
Supports accessibility for: Organization; Visual-spatial processing
Design Principle(s): Support sense-making
Student Facing
-
Find the value of each expression. Show your reasoning.
- \(11.3 - 9.5\)
- \(318.8 - 94.63\)
- \(0.02 - 0.0116\)
-
Discuss with a partner:
- Which method or methods did you use in the previous question? Why?
- In what ways were your methods effective? Was there an expression for which your methods did not work as well as expected?
- Lin’s grandmother ordered needles that were 0.3125 inches long to administer her medication, but the pharmacist sent her needles that were 0.6875 inches long. How much longer were these needles than the ones she ordered? Show your reasoning.
- There is 0.162 liter of water in a 1-liter bottle. How much more water should be put in the bottle so it contains exactly 1 liter? Show your reasoning.
- One micrometer is 1 millionth of a meter. A red blood cell is about 7.5 micrometers in diameter. A coarse grain of sand is about 70 micrometers in diameter. Find the difference between the two diameters in meters. Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may benefit from using graph paper for calculations; they can place one digit in each box for proper decimal point placement and place value unit alignment. For the last question, students might confuse the amount of zeros in 1 millionth. It might be helpful to write 0.000001 on the board as reference.
Activity Synthesis
Discussions on the first 2 questions are outlined in the Launch section. Focus the discussion here on the last 3 questions, i.e., on how students interpreted the problems, determined which operation to perform, and found the sum or difference (including how they handled any regroupings). Select a few previously identified students to share their responses and reasoning.
If some students chose base-ten diagrams for the calculation, contrast its efficiency with that of numerical calculations. The numbers in these problems have enough decimal places that using base-ten representations (physical blocks, drawings, or digital representations) would be cumbersome, making a numerical calculation appealing.
4.3: Missing Numbers (15 minutes)
Activity
Students deepen their understanding of regrouping by tackling problems that are more challenging and that prompt them to notice and use structure (MP7). Students build on both their work with whole-number differences (such as \(1,\!000 - 256\)) to find differences such as \(1 - 0.256\). To add and subtract digits, they may think in terms of bundling and unbundling base-ten units, but there are also other opportunities to use structure here. Let’s take the example \(1,\!000 - 256\). Since \(1,\!000 = 999 + 1\), students could calculate \(1,\!000 - 256\) by first finding \(999 - 256 = 743\), and then adding 1 to get \(744\). They could use the same reasoning to find sums and differences of decimals.
As students work and discuss their responses, notice the different ways students reason about the addition and subtraction. Identify a few students with differing approaches to share later.
Launch
Arrange students in groups of 2. Give students 8–10 minutes of quiet work time and 2–3 minutes to discuss their answers with a partner. Follow with a whole-class discussion.
Student Facing
Write the missing digits in each calculation so that the value of each sum or difference is correct. Be prepared to explain your reasoning.
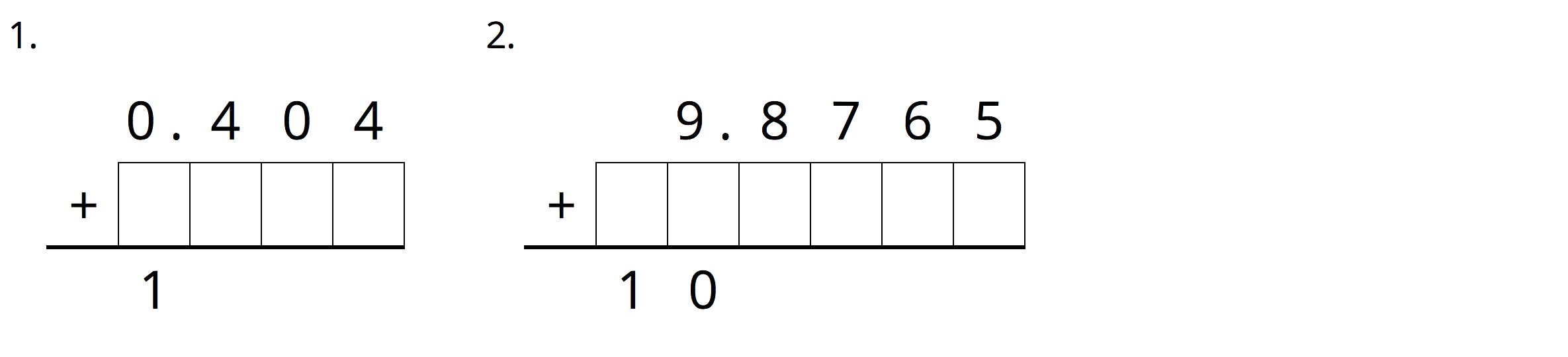
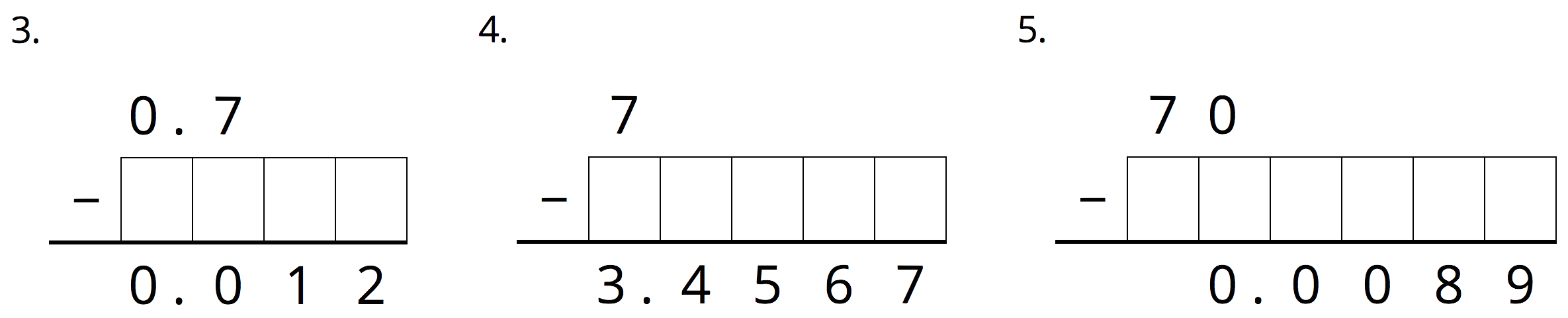
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
In a cryptarithmetic puzzle, the digits 0-9 are represented using the first 10 letters of the alphabet. Use your understanding of decimal addition to determine which digits go with the letters A, B, C, D, E, F, G, H, I, and J. How many possibilities can you find?
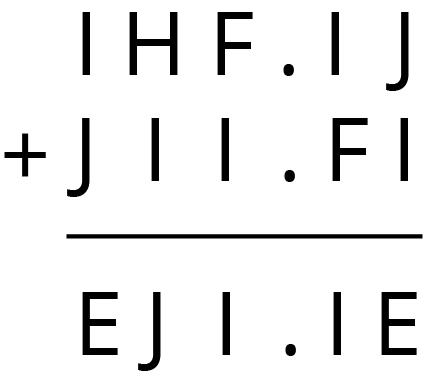
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students use a guess-and-check method without success, encourage them to try working backwards. Consider scaffolding with a simpler problem involving whole numbers, such as \(10 - {?} = 3\). We can find the answer by thinking: \(3+{?}=10\), or \(10-3={?}\).
Activity Synthesis
Select previously identified students to share their responses. Ask students how they approached the addition and subtraction problems, whether they work backwards, write additional zeros, or use other strategies to find the missing numbers.
Conclude the discussion by asking students how their work would change in the fourth question (\(7 - {?} = 3.4567\)) if they were to replace 7 with 6.9999. Give students a moment to think about the question, and then ask:
- “How might the number 6.9999 help us find the missing number?” (The 9s make it easier to find each missing digit, so we can find the difference between 6.9999 and 3.4567, and then add 0.0001 to the result because 6.9999 is 0.0001 less than 7.)
- “How would this method work for a problem such as the second question: \(9.8765 + {?} = 10\)?” (We can replace 10 with 9.9999, determine the missing number, and then add 0.0001 to that number).
This strategy is effective because it eliminates the “extra zeros” and the need to compose or decompose.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
In this lesson, students practiced adding and subtracting numbers with many decimal places, both in and outside of the context of situations. They noticed the benefits of vertical calculations and used its structure to solve problems.
- Which problems did you solve with addition (or subtraction)? How did you know to use addition (or subtraction)?
- How did you find the sums or differences? Why did you choose that method?
- Did you use the same method for all problems? Why or why not?
- When subtracting a number with fewer decimal places by another number with more decimal places, such as \(2.4 - 0.1587\), what strategies might be helpful? (We can think of 2.4 as 2.4000 and use unbundling to subtract 0.1587 from it. Or we can think of the 2.4 as \(2.3999 + 0.0001\), line up and subtract 0.1587 from 2.3999, and then add 0.0001 back to the difference.)
4.4: Cool-down - Taller and Farther (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Base-ten diagrams work best for representing subtraction of numbers with few non-zero digits, such as \(0.16 - 0.09\). For numbers with many non-zero digits, such as \(0.25103 - 0.04671\), it would take a long time to draw the base-ten diagram. With vertical calculations, we can find this difference efficiently.
Thinking about base-ten diagrams can help us make sense of this calculation.
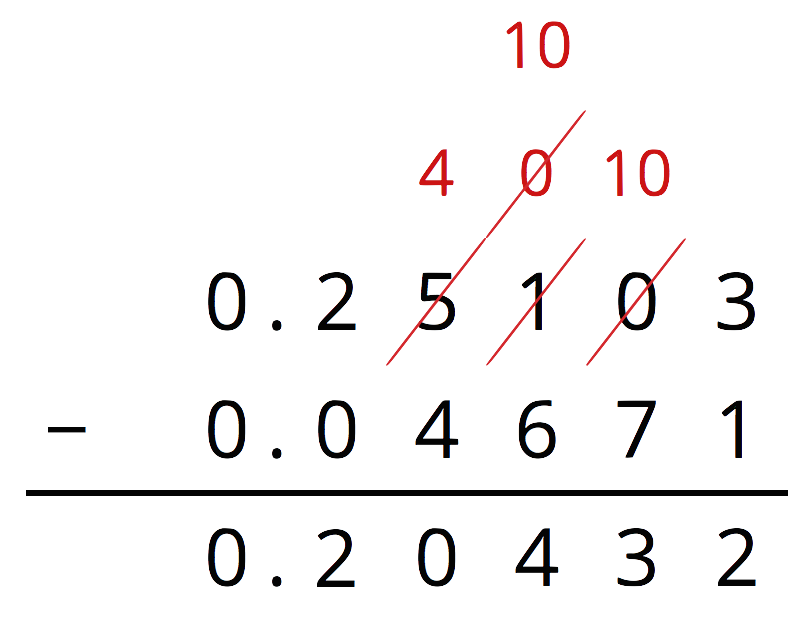
The thousandth in 0.25103 is unbundled (or decomposed) to make 10 ten-thousandths so that we can subtract 7 ten-thousandths. Similarly, one of the hundredths in 0.25103 is unbundled (or decomposed) to make 10 thousandths.