Lesson 10
Using Long Division
10.1: Number Talk: Estimating Quotients (5 minutes)
Warm-up
This number talk prompts students to make reasonable estimates of quotients using their knowledge of numbers, division, and structures. Only two problems are given to allow more time for students to share their estimation strategies.
Making reasonable estimates helps to develop arithmetic fluency. Here, it relies on understanding the relationship between multiplication and division, and on the different properties of operations (commutative, associative, and distributive). For example, to find \(500 \div 7\), students might think of the multiplication equation \(7 \boldcdot {?} = 500\). Since they know that \(7 \boldcdot 100 = 700\) and \(7 \boldcdot 30 = 210\), and that \(500 = 700-200\), they could reason that 500 would be approximately \(7 \boldcdot (100-30)\) or \(7 \boldcdot 70\).
Launch
Display each problem one at a time for all to see. Give students 1 minute of quiet think time and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Estimate these quotients mentally.
\(500 \div 7\)
\(1,\!394 \div 9\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might try to calculate exact answers and take longer to produce an answer. Encourage them to approximate the actual answer by rounding the dividend or divisor or starting with friendlier numbers.
Activity Synthesis
Invite students to share their strategies. Record and display student explanations for all to see. Ask students to explain if or how the dividend or divisor impacted their choice of strategy. To involve more students in the conversation, consider asking:
- “Did anyone reason about the problem the same way but would explain it differently?”
- “Did anyone estimate in a different way?”
- “Does anyone want to add on to _____’s reasoning?”
- “Do you agree or disagree? Why?”
At the end of the discussion, if time permits, ask a few students to share a story problem or context that \(1,394 \div 9\) could represent.
Design Principle(s): Optimize output (for explanation)
10.2: Lin Uses Long Division (25 minutes)
Activity
This activity introduces the use of long division to calculate a quotient of whole numbers. Students make sense of the process of long division by studying an annotated example and relating it to the use of partial quotients and base-ten diagrams. They begin to see that long division is a variant of the partial quotients method, but it is calculated and recorded differently.
In the partial quotients method, the division is done in installments, resulting in a series of partial quotients. The size of each installment can vary, but it is always a multiple of the divisor. Each partial quotient is written above the dividend and stacked; the sum of all partial quotients is the quotient.
In long division, the division is performed digit by digit, from the largest place to the smallest, so the resulting quotient is also recorded one digit at a time. In each step, one more digit of the quotient is calculated. Students notice that although only one digit of the quotient is written down at a time, the value that it represents is communicated through its placement.
To become proficient in long division requires time, encounters with a variety of division problems, and considerable practice. Students will have opportunities to study the algorithm more closely and to use it to divide increasingly more challenging numbers over several upcoming lessons.
Launch
Tell students that they will now consider a third method—called long division—for solving the same division problem that Elena and Andre had calculated using base-ten diagrams and the partial quotients method. Encourage students to refer to their work on those activities, or display Elena and Andre’s methods for all to see. Ask a couple of students to briefly explain how Elena and Andre calculated \(657 \div 3\).
Arrange students in groups of 2. Give students 2–3 minutes of quiet think time to make sense of the annotated example of long division, and then 3–4 minutes to discuss the first set of questions with a partner. Follow with a whole-class discussion before students use long division to answer the second set of questions.
Display Lin’s method for all to see and ask a student to explain what Lin had done in his or her own words. Then, discuss students’ responses to the first set of questions and these questions:
-
In the first step, Lin divided 6 by 3 to get 2. Did it matter where Lin wrote the 2? Why did she put it over the 6? (Yes, it mattered. Because the 6 represents 600, she was really dividing 600 by 3, which is 200. The 2 needs to be written in the hundreds place to tell us its actual value.)
-
After writing down the 2, Lin subtracted 6. Why? And why was the result of the subtraction not 651 (since \(657-6=651\))? (Though she wrote a subtraction of 6, she actually subtracted 600. Because she had just divided 600 by 3, that portion of 657 is already accounted for.)
-
Could Lin have written the full amounts being subtracted instead of just the non-zero digit (e.g., subtracting by 600, 50 and 7, instead of subtracting by 6, 5, and 7 after aligning them to certain places)? (Yes, it would involve more writing, but it works just as well.)
-
How is this process similar to and different than the partial quotients method? (It is a similar idea of taking out a certain multiple of 3 at a time, but in long division we do it digit by digit and in the order of place value—from the largest unit to the smallest.)
Consider demonstrating the long-division process with another example such as \(912 \div 4\) before asking students to complete the rest of the task. Provide access to graph paper. Tell students that the grid could help them line up the digits.
Supports accessibility for: Language
Student Facing
Lin has a method of calculating quotients that is different from Elena’s method and Andre’s method. Here is how she found the quotient of \(657\div 3\):
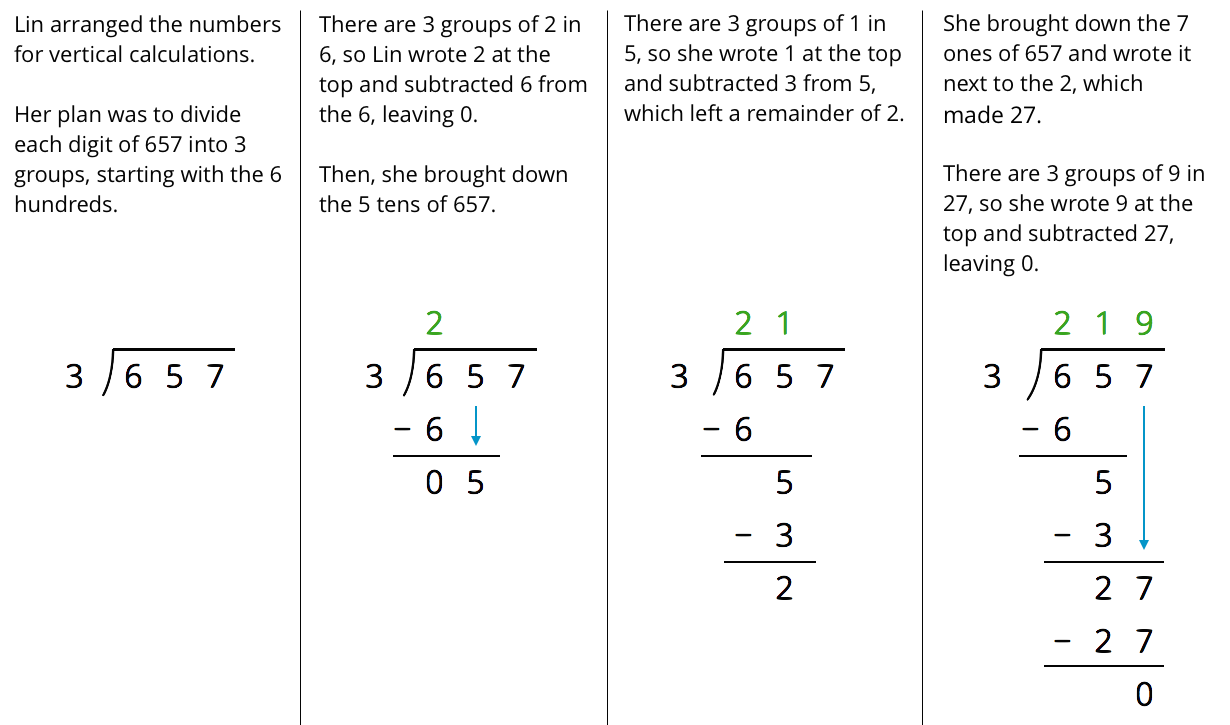
-
Discuss with your partner how Lin’s method is similar to and different from drawing base-ten diagrams or using the partial quotients method.
- Lin subtracted \( 3 \boldcdot 2,\) then \(3 \boldcdot 1\), and lastly \(3 \boldcdot 9\). Earlier, Andre subtracted \(3 \boldcdot 200,\) then \(3 \boldcdot 10\), and lastly \(3 \boldcdot 9\). Why did they have the same quotient?
- In the third step, why do you think Lin wrote the 7 next to the remainder of 2 rather than adding 7 and 2 to get 9?
-
Lin’s method is called long division. Use this method to find the following quotients. Check your answer by multiplying it by the divisor.
- \(846 \div 3\)
- \(1,\!816 \div 4\)
- \(768 \div 12\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Display the worked-out long divisions for all to see. Select a student to explain the steps for at least one of the division problems. Highlight two ideas about long division: 1) we start by dividing the largest base-ten units and work toward smaller units, and 2) the placement of each digit of the quotient matters because it conveys the value of the digit.

Draw students’ attention to the second problem (\(1,\!816 \div 4\)) or third problem (\(768 \div 12\)), in which the first digit of the dividend is smaller than the divisor. Select 1–2 students to share how they approached these situations. If not brought up in students’ explanation, discuss how we could reason about these.
-
“Let’s take \(1,\!816 \div 4\) as an example. If we were using base-ten diagrams, we would have 1 piece representing a thousand. How would we divide that piece into 4 groups?” (We would unbundle it into 10 hundreds, add them to the 8 pieces representing 8 hundreds, and then distribute the 18 hundreds into 4 groups.)
-
“How can we apply the same idea to long division? If there is not enough thousands to divide into 4 groups, what can we do?” (We can think of the 1 thousand and 8 hundreds as 18 hundreds and divide that value instead.)
-
“How many hundreds would go into each group if we divide 18 hundreds into 4 groups?” (4 hundreds, with a remainder of 2 hundreds.)
-
“Where should we write the 4? Why?” (In the hundreds place, because it represents 4 hundreds.)
-
“How do we deal with the 2 hundreds?” (Since there is not enough to distribute into 4 groups, we can unbundle them into 20 tens, combine them with the 1 ten, and divide 21 tens by 4.)
Design Principle(s): Optimize output (for justification); Cultivate conversation
10.3: Dividing Whole Numbers (10 minutes)
Optional activity
In this activity, students continue to practice using long division to find quotients. Here, the presence of 0’s in the dividend and the quotient presents an added layer of complexity, prompting students to really make sense of the the meaning of each digit in numbers they are dealing with (MP7).
Launch
Give students 6–7 minutes of quiet work time. Follow with a whole-class discussion. Provide access to graph paper.
Supports accessibility for: Language; Social-emotional skills
Student Facing
-
Find each quotient.
- \(633 \div 3\)
- \(1001 \div 7\)
- \(2996\div14\)
-
Here is Priya’s calculation of \(906 \div 3\).
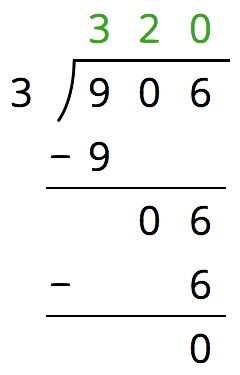
- Priya wrote 320 for the value of \(906 \div 3\). Check her answer by multiplying it by 3. What product do you get and what does it tell you about Priya’s answer?
- Describe Priya’s mistake, then show the correct calculation and answer.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Focus class discussion on attending to the meaning of each digit in performing division. Discuss:
-
How did you deal with the 0’s in 1,001? Would they cause any difficulty when doing long division? (I brought down the first 0 and then performed division like I would have done with any other digit. After subtracting one 7 from 10, I was left with 3. Putting a 0 after the 3 changes the value to 30. So even though the 0 alone has no value, it changes the value of the numbers in front of it).
-
How can you check your answer to a division problem such as \(1,\!001 \div 147\)? (We can check by multiplying the quotient by the divisor. If the division was done correctly, then \(143 \boldcdot 7 = 1,\!001\), which is true).
-
What happens if you check Priya’s answer for \(906 \div 3\)? (\(320 \boldcdot 3 = 960\), so this tells us that Priya’s answer is incorrect).
Make sure students notice that although checking an answer can tell you that you have made a mistake, it will not necessarily identify where the mistake is. It only works if you perform the multiplication correctly.
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Long division is another method for finding quotients. It follows similar lines of reasoning for dividing with base-ten diagrams or using the partial quotients method. All three methods rely on the structure of the base-ten number system.
-
How is dividing using long division similar to dividing by drawing base-ten diagrams? (Even though one method involves drawing and the other involves using only numbers, they rely on the same principle of dividing base-ten units into equal-sized groups. In both methods, when there is not enough of a unit to divide equally into groups, we can unbundle the unit into the next smaller base-ten units.)
-
How is long division similar to and different from the partial quotients method? (They are similar in that we divide in “installments,” but in the partial quotients method, we can decide on the size of each installment or each group being subtracted from the dividend. In long division, we follow a very specific order based on place value and we divide digit by digit—from left to right, and subtract as large a group as possible at any step. In long division, we also do not write out all the numbers in our calculations; we use one digit at a time and rely on its place in the base-ten system to convey its value.)
-
Which method for finding quotients do you think is the most efficient? (It depends on the numbers involved. If the numbers are large or long, drawing would be laborious and prone to error, and using partial quotients might mean a whole lot of steps. Long division might be simpler because we are reasoning with one digit and one place-value unit at a time.)
10.4: Cool-down - Dividing by 15 (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Long division is another method for calculating quotients. It relies on place value to perform and record the division.
When we use long division, we work from left to right and with one digit at a time, starting with the leftmost digit of the dividend. We remove the largest group possible each time, using the placement of the digit to indicate the size of each group. Here is an example of how to find \(948 \div 3\) using long division.
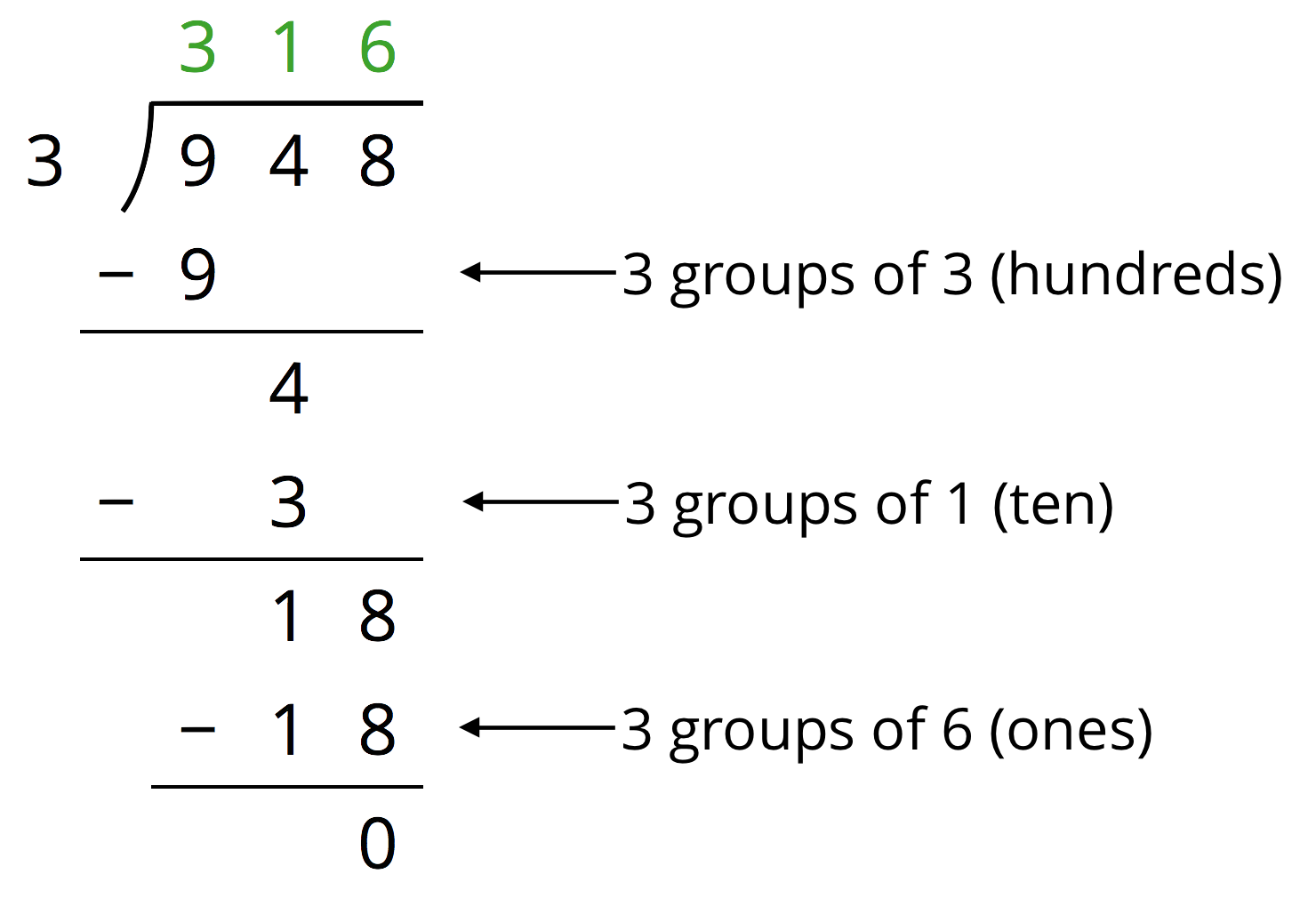
-
We start by dividing 9 hundreds into 3 groups, which means 3 hundreds in each group. Instead of writing 300, we simply write 3 in the hundreds place, knowing that it means 3 hundreds.
-
There are no remaining hundreds, so we work with the tens. We can make 3 groups of 1 ten in 4 tens, so we write 1 in the tens place above the 4 of 948. Subtracting 3 tens from 4 tens, we have a remainder of 1 ten.
-
We know that 1 ten is 10 ones. Combining these with the 8 ones from 948, we have 18 ones. We can make 3 groups of 6, so we write 6 in the ones place.
In total, there are 3 groups of 3 hundreds, 1 ten, and 6 ones in 948, so \(948 \div 3 = 316\).