Lesson 12
Dividing Decimals by Whole Numbers
12.1: Number Talk: Dividing by 4 (5 minutes)
Warm-up
The purpose of this number talk is to help students use the structure of base-ten numbers and the distributive property to solve a division problem involving decimals.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all problems displayed throughout the talk. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find each quotient mentally.
\(80 \div 4\)
\(12 \div 4\)
\(1.2 \div 4\)
\(81.2 \div 4\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone have the same strategy but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
Highlight the use of the distributive property in finding \(81.2 \div 4\). Students should recognize that since \(81.2=80+1.2\), we have \(81.2\div 4=(80\div 4)+(1.2\div 4)\). To make this clear, consider explaining that the division could be equivalently represented by \(81.2\boldcdot \frac14=(80+1.2)\boldcdot\frac14=(80\boldcdot \frac14)+(1.2\boldcdot\frac14)\).
Design Principle(s): Optimize output (for explanation)
12.2: Using Diagrams to Represent Division (15 minutes)
Activity
Students have learned several effective methods to divide a whole number by a whole number, including cases when there is a remainder. The goal of this task is to introduce a method for dividing a decimal number by a whole number. Students notice that the steps in the division process are the same as when dividing a whole number by a whole number, whether the division is done with base-ten diagrams, as in this task, or using partial quotients or the division algorithm as in future tasks. Here, students need to think even more carefully about place value and where the decimal point goes in the quotient.
Throughout this activity, students rely on their understanding of equivalent expressions to interpret the unbundling in Elena’s process. For example, to unbundle a one into ten tenths means going between the expressions 1 and \(0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1\).
Launch
Give students 1–2 minutes of quiet think time for students to analyze Elena’s work. Pause and discuss with the whole class. Select a couple of students to share their analyses of what Elena had done to divide a decimal by a whole number. Then, give students 8–9 minutes to complete the questions and follow with a whole-class discussion.
Student Facing
To find \(53.8 \div 4\) using diagrams, Elena began by representing 53.8.

She placed 1 ten into each group, unbundled the remaining 1 ten into 10 ones, and went on distributing the units.
This diagram shows Elena’s initial placement of the units and the unbundling of 1 ten.

-
Complete the diagram by continuing the division process. How would you use the available units to make 4 equal groups?
As the units get placed into groups, show them accordingly and cross out those pieces from the bottom. If you unbundle a unit, draw the resulting pieces.
-
What value did you find for \(53.8 \div 4\)? Be prepared to explain your reasoning.
-
Use long division to find \(53.8 \div 4\). Check your answer by multiplying it by the divisor 4.
-
Use long division to find \(77.4 \div 5\). If you get stuck, you can draw diagrams or use another method.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.
A group of 4 craftsmen are paid 1 of each jewel. If they split the jewels evenly amongst themselves, which jewels does each craftsman get?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may stop dividing when they reach a remainder rather than unbundling the remainder into smaller units. Remind them that they can continue to divide the remainder by unbundling and to refer to Elena’s worked-out example or those from earlier lessons, if needed.
Activity Synthesis
Ask a student or two to display and explain their work. Ask if others performed the division the same way and if there are disagreements.
Then, focus the discussion on the connections between a division problem with a whole-number dividend (such as \(62 \div 5\)) and that with a decimal dividend (such as \(53.8 \div 4\)). Discuss:
- How is the division problem \(53.8 \div 4\) similar to \(62 \div 5\) from a previous lesson?
- In both problems, when we get to the final place value (tenths for \(53.8 \div 4\) and one for \(62 \div 5\)), there is still a remainder.
- In both problems, to complete the division and find the quotient we need to introduce a new place value (hundredths for \(53.8 \div 4\), and tenths for \(62 \div 5\)).
- We have to unbundle at every step in both division problems.
- How is the division problem \(53.8 \div 4\) different to \(62 \div 5\) from a previous lesson?
- There is already a decimal in \(53.8\): we had to write the decimal point for \(62 \div 5\).
- The quotient \(53.8 \div 4\) goes to the hundredths place, so there is an extra step and an additional place value.
If we were to rewrite \(62 \div 5\) as \(62.0 \div 5\) (which is what is needed in order to complete the division), then the two division problems look similar. The biggest difference between \(53.8 \div 4\) and \(62 \div 5\) is that the former problem has an answer in the hundredths while the answer to the latter only has tenths.
Design Principle(s): Support sense-making; Maximize meta-awareness
12.3: Dividends and Divisors (15 minutes)
Activity
In this activity, students study some carefully chosen quotients where the dividends are decimal numbers. The key goal here is to notice that there are other quotients of whole numbers that are equivalent to these quotients of decimals. In other words, when the dividend is a terminating decimal number, we can find an equivalent quotient whose dividend is a whole number. In combination with the previous task, this gives students the tools they need to divide a decimal number by a decimal number.
This activity strongly supports MP7. Students notice that, when working with a fraction, multiplying the numerator and denominator in a fraction by 10 does not change the value of the fraction. They use this insight to develop a way to divide decimal numbers in subsequent activities. This work develops students’ understanding of equivalent expressions by emphasizing that, for example, \(8\div 1= (8\boldcdot 10) \div (1\boldcdot 10)\). Eventually, students will recognize the equivalence of \(8\div 1\) to statements such as \((8\boldcdot y)\div (1\boldcdot y)\). However, in this activity, students only examine situations where the dividend and divisor are multiplied by powers of 10.
Launch
Display the following image of division calculations for all to see.
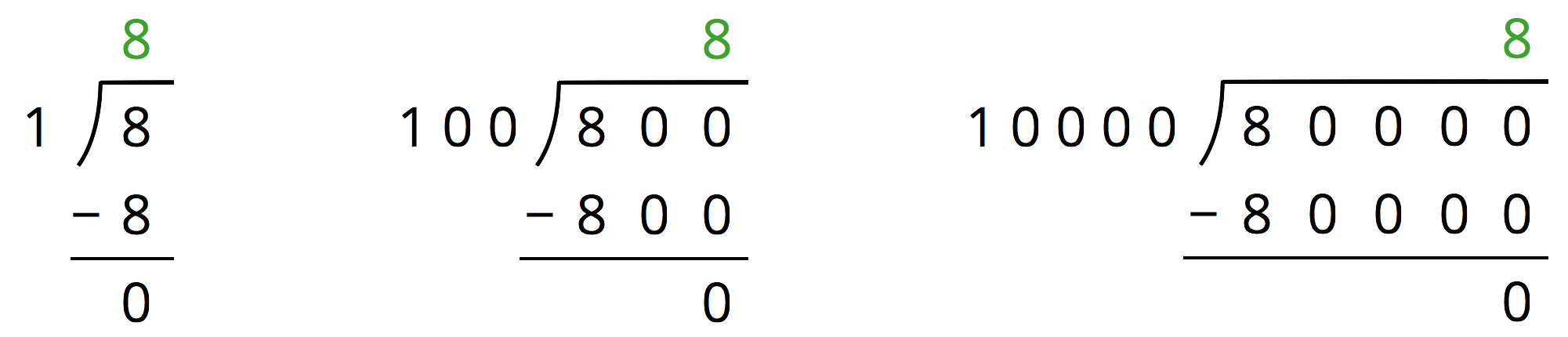
Ask students what quotient each calculation shows. (\(8 \div 1\), \(800 \div 100\), and \(80,\!000 \div 10,\!000\)). Give students 1–2 minutes to notice and wonder about the dividends, divisors, and quotients in the three calculations. Ask them to give a signal when they have at least one observation and one question. If needed, remind students that the 8, 800, and 80,000 are the dividends and the 1, 100, and 10,000 are the divisors.
Invite a few students to share their observations and questions. They are likely to notice:
- Each calculation shows that the value of the corresponding quotient is 8; it is the same for all three calculations.
- All calculations have an 8 in the dividend and a 1 in the divisor.
- All calculations take one step to solve.
- Each divisor is 100 times the one to the left of it.
- Each dividend is 100 times the one to the left of it.
- Each dividend and each divisor have 2 more zeros than in the calculation immediately to their left.
They may wonder:
- Why are the quotients equal even though the divisors and dividends are different?
- Would \(80 \div 10\) and \(8,\!000 \div 10\) also produce a quotient of 8?
- Are there other division expressions with an 8 in the dividend and a 1 in the divisor and no other digits but zeros that would also produce a quotient of 8?
Without answering their questions, tell students that they’ll analyze the sizes of dividends and divisors more closely to help them reason about quotients of numbers in base ten.
Give students 7–8 minutes of quiet work time to answer the four questions followed by a whole-class discussion.
Supports accessibility for: Organization; Attention
Student Facing
Analyze the dividends, divisors, and quotients in the calculations, and then answer the questions.
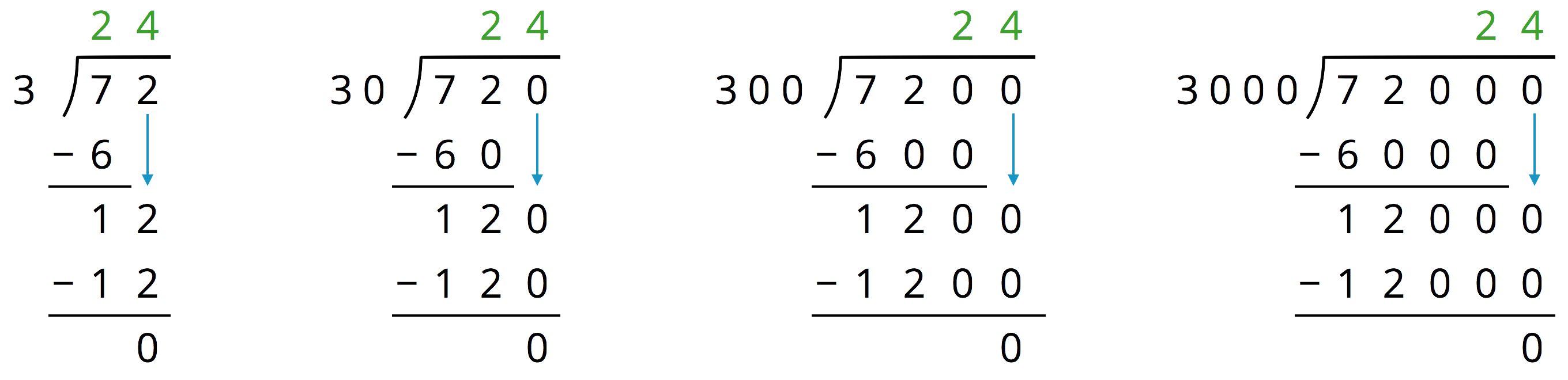
-
Complete each sentence. In the calculations shown:
-
Each dividend is ______ times the dividend to the left of it.
-
Each divisor is ______ times the divisor to the left of it.
-
Each quotient is _____________________ the quotient to the left of it.
-
-
Suppose we are writing a calculation to the right of \(72,\!000 \div 3,\!000\). Which expression has a quotient of 24? Be prepared to explain your reasoning.
- \(72,\!000 \div 30,\!000\)
- \(720,\!000 \div 300,\!000\)
- \(720,\!000 \div 30,\!000\)
- \(720,\!000 \div 3,\!000\)
- Suppose we are writing a calculation to the left of \(72 \div 3\). Write an expression that would also give a quotient of 24. Be prepared to explain your reasoning.
-
Decide which of the following expressions would have the same value as \(250 \div 10\). Be prepared to share your reasoning.
- \(250 \div 0.1\)
- \(25 \div 1\)
- \(2.5 \div 1\)
- \(2.5 \div 0.1\)
- \(2,500 \div 100\)
- \(0.25 \div 0.01\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to write a reflection using the following prompt:
What happens to the value of the quotient when both the divisor and the dividend are multiplied by the same power of 10? Use examples to show your thinking.
The goal of this discussion is to make sure students understand that the value of a quotient does not change when both the divisor and the dividend are multiplied by the same power of ten. Ask students to explain why \(\frac{25}{20} = \frac{250}{200}\). Possible responses include:
- Both the numerator and denominator of \(\frac{250}{200}\) have a factor of 10, so the fraction can be written as \(\frac{25}{20}\).
- Both fractions are equivalent to \(\frac{5}{4}\).
- Dividing 250 by 200 and 25 by 20 both give a value of 1.25.
Tell students that their observations here will help them divide decimals in upcoming activities.
Design Principles(s): Cultivate conversation; Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
In this lesson, we saw that we can divide a decimal by a whole number the same way we divide two whole numbers. We used base-ten diagrams to show how this is true.
- How do we use base-ten diagrams to show division of a decimal by a whole number, for example, \(0.8 \div 5\)? (We can draw eight of a type of figures to represent 8 tenths and distribute them into 5 groups.)
- What do we do with remainders? For example, in the case of \(0.8 \div 5\), how do we deal with the remainder of 3 tenths? (We can unbundle each tenth into 10 hundredths and distribute the 30 hundredths into 5 equal groups. Each group would have 6 hundredths.)
- How do we know what the quotient of \(0.8 \div 5\) is? (It is the value of each group: 1 tenth and 6 hundredths, or 0.16.)
We also thought about division of decimals a different way—by multiplying both the dividend and divisor by the same power of 10, which gives us an equivalent division expression.
- What are some division expressions that are equivalent to \(30 \div 0.1\)? (\(300 \div 1\); \(3,\!000 \div 10\))
- What happens to the value of a quotient when both the divisor and the dividend are multiplied by the same power of 10? (The value does not change.)
12.4: Cool-down - The Same Quotient (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We know that fractions such as \(\frac 64\) and \(\frac {60}{40}\) are equivalent because:
- The numerator and denominator of \(\frac {60}{40}\) are each 10 times those of \(\frac 64\).
- Both fractions can be simplified to \(\frac 32\).
- 600 divided by 400 is 1.5, and 60 divided by 40 is also 1.5.
Just like fractions, division expressions can be equivalent. For example, the expressions \(540 \div 90\) and \(5,\!400 \div 900\) are both equivalent to \(54 \div 9\) because:
- They all have a quotient of 6.
- The dividend and the divisor in \(540 \div 90\) are each 10 times the dividend and divisor in \(54 \div 9\). Those in \(5,\!400 \div 900\) are each 100 times the dividend and divisor in \(54 \div 9\). In both cases, the quotient does not change.
This means that an expression such as \(5.4 \div 0.9\) also has the same value as \(54 \div 9\). Both the dividend and divisor of \(5.4 \div 0.9\) are \(\frac {1}{10}\) of those in \(54 \div 9\).
In general, multiplying a dividend and a divisor by the same number does not change the quotient. Multiplying by powers of 10 (e.g., 10, 100, 1,000, etc.) can be particularly useful for dividing decimals, as we will see in an upcoming lesson.