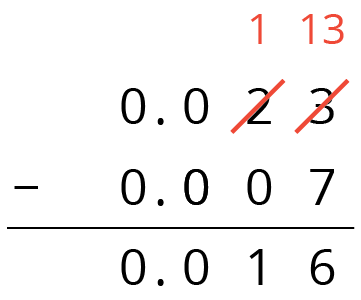Lesson 3
Adding and Subtracting Decimals with Few Non-Zero Digits
3.1: Do the Zeros Matter? (5 minutes)
Warm-up
This warm-up prompts students to reason about regrouping and about when the zeros in a decimal affect the number that it represents. The mathematical work of interest is how students combine two decimals (e.g., in analyzing \(1.009 + 0.391\), do they see that \(0.009 + 0.001 = 0.010\)?) and how they write the sum (e.g., do they know \(1.4=1.40=1.400\)?).
Launch
Arrange students in groups of 2. Give students 1 minute of quiet time to mentally add the decimals in the first problem and then another minute to discuss their answer and strategy with a partner. Briefly discuss their strategies as a class, and then ask students to complete the true-or-false questions.
Student Facing
-
Evaluate mentally: \(1.009+0.391\)
-
Decide if each equation is true or false. Be prepared to explain your reasoning.
- \(34.56000 = 34.56\)
- \(25 = 25.0\)
- \(2.405 = 2.45\)
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may say, “You can take the zeros away after the decimal point and the number stays the same.” Although students could mean, for instance, that 12.9 is equal to 12.90, they might also mistakenly think 12.09 is equal 12.9. Ask these students to be more precise in their statement. Ask if the zero can be in any place after the decimal point or only in certain places.
Activity Synthesis
Ask students to indicate whether they think each equation is true or false and ask for an explanation for each. Students may simply say that we can or cannot just remove the zeros. Encourage them to use what they know about place values or comparison strategies to explain why one number is greater than, less than, or equal to the other. If students do not notice that the two numbers in the true-or-false questions have the same digits except for the missing zeros, point that out after each question.
If not mentioned by students in their explanations, ask:
- “Can zeros be written at the end of a decimal without changing the number that it represents?”
- “Can zeros be eliminated from the end of a decimal without changing the value?”
- “Can zeros be written or erased in the middle of a decimal without changing the value?”
3.2: Calculating Sums (15 minutes)
Optional activity
Here students continue to use diagrams to represent sums of decimals, but they also transition to writing addition calculations vertically. They think about the alignment of the digits in vertical calculations to help ensure that correct values are combined. This activity is optional, so students have the option to spend more time subtracting decimals in the next activity.
As in the previous activity, consider having students use physical base-ten blocks (if available), a paper version of the base-ten figures (from the blackline master), or this digital applet ggbm.at/FXEZD466, as alternatives to drawing diagrams.
Launch
Remind students that the term “sum” means the result of an addition. Refer to the image from the previous activity that shows how several squares and rectangles were used to represent base-ten units. Tell students to use the same representations in this activity and to keep in mind that in the process of bundling they find more sums of decimals.
Arrange students in groups of 2. Give students 10 minutes of quiet work time, but encourage them to briefly discuss their responses with their partner after completing the second question and before continuing with the rest. Follow with a whole-class discussion.
Classes using the digital activities have an interactive applet with virtual blocks. In this activity, students must redefine the value of each block to represent the place values in each problem. To use the bundling and unbundling features, the pieces must be aligned on the light blue grids. To bring a piece into the workspace, select one of the green tool icons and then click on the workspace. To move it, you must click on the Move tool (the arrow).

Supports accessibility for: Conceptual processing
Design Principle(s): Optimize output (for justification)
Student Facing
-
Andre and Jada drew base-ten diagrams to represent \(0.007 + 0.004\). Andre drew 11 small rectangles. Jada drew only two figures: a square and a small rectangle.

- If both students represented the sum correctly, what value does each small rectangle represent? What value does each square represent?
- Draw or describe a diagram that could represent the sum \(0.008 + 0.07\).
-
Here are two calculations of \(0.2 + 0.05\). Which is correct? Explain why one is correct and the other is incorrect.

- Compute each sum. If you get stuck, consider drawing base-ten diagrams to help you.
-
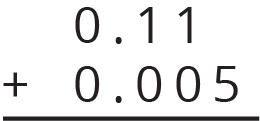
- \(0.209 + 0.01\)
- \(10.2 + 1.1456\)
-
- The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
- Select a Block tool, and then click on the screen to place it.
- Click on the Move tool (the arrow) when you are done choosing blocks.
- Subtract by deleting with the delete tool (the trash can), not by crossing out.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Remind students that the term “sum” means the result of an addition. Refer to the image from the previous activity that shows how several squares and rectangles were used to represent base-ten units. Tell students to use the same representations in this activity and to keep in mind that in the process of bundling they find more sums of decimals.
Arrange students in groups of 2. Give students 10 minutes of quiet work time, but encourage them to briefly discuss their responses with their partner after completing the second question and before continuing with the rest. Follow with a whole-class discussion.

Supports accessibility for: Conceptual processing
Design Principle(s): Optimize output (for justification)
Student Facing
-
Andre and Jada drew base-ten diagrams to represent \(0.007 + 0.004\). Andre drew 11 small rectangles. Jada drew only two figures: a square and a small rectangle.

- If both students represented the sum correctly, what value does each small rectangle represent? What value does each square represent?
- Draw or describe a diagram that could represent the sum \(0.008 + 0.07\).
-
Here are two calculations of \(0.2 + 0.05\). Which is correct? Explain why one is correct and the other is incorrect.

- Compute each sum. If you get stuck, consider drawing base-ten diagrams to help you.
-
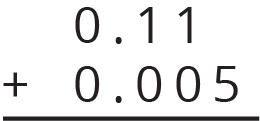
- \(0.209 + 0.01\)
- \(10.2 + 1.1456\)
-
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The goal of this discussion is to help students understand that vertical calculation is an efficient way to find the sums of decimals. Discuss:
- “When finding \(0.008 + 0.07\), why do we not combine the 8 thousandths and 7 hundredths to make 15?” (Hundredths and thousandths are different units. If each hundredth is unbundled into 10 thousandths, we can add 70 thousandths and 8 thousandths to get 78 thousandths).
- “How do we use representations of base-ten numbers to add effectively and efficiently?” (Make sure to put together tenths with tenths, hundredths with hundredths, etc. Also, make sure that if a large square represents \(\frac{1}{10}\) for one summand, it also represents \(\frac{1}{10}\) for the other.)
- “When adding numbers without using base-ten diagrams or other representations, what can we do to help add them correctly?” (Pay close attention to place value so we combine only like units. It is helpful to line up the digits of the numbers so that numerals that represent the same place value are placed directly on top of one another.)
Additionally, consider using color coding to help students visualize the place-value structure, as shown here.
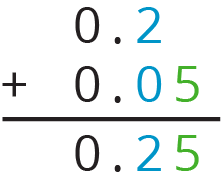
3.3: Subtracting Decimals of Different Lengths (25 minutes)
Activity
In this activity, students encounter two variations of decimal subtraction in which regrouping is involved. They subtract a number with more decimal places from one with fewer decimal places (e.g., \(0.1 - 0.035\)), and subtract two digits that represent the same place value but where the value in the second number is greater than that in the starting number (e.g., in \(1.12 - 0.47\), both the tenth and hundredth values in the second number is larger than those in the first).
Students represent these situations with base-ten diagrams and study how to perform them using vertical calculations. The big idea here is that of “unbundling” or of decomposing a unit with 10 of another unit that is \(\frac{1}{10}\) its size to make it easier to subtract. In some cases, students would need to decompose twice before subtracting (e.g., a tenth into 10 hundredths, and then 1 hundredth into 10 thousandths).
Use the whole-class discussion to highlight the correspondences between the two methods and to illustrate how writing zeros at the end of a decimal helps us perform subtraction.
As in previous activities, consider having students use physical base-ten blocks (if available), a paper version of the base-ten figures (from the blackline master), or this digital applet https://ggbm.at/FXEZD466, as alternatives to drawing diagrams.
Launch
Keep students in the same groups of 2. Give partners 4–5 minutes to complete the first two questions. Then, give students 4–5 minutes of quiet time to complete the last question and follow with a whole-class discussion.


Use MLR2 (Collect and Display) to listen for and capture two or three different ways students refer to the idea of “unbundling” as they work on problems 1 and 2.
Supports accessibility for: Conceptual processing
Student Facing
To represent \(0.4 - 0.03\), Diego and Noah drew different diagrams. Each rectangle represented 0.1. Each square represented 0.01.
-
Diego started by drawing 4 rectangles to represent 0.4. He then replaced 1 rectangle with 10 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 3 rectangles and 7 squares in his diagram.
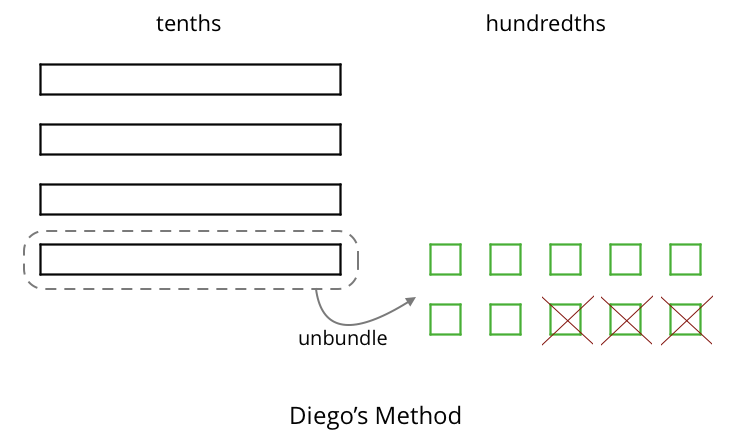
-
Noah started by drawing 4 rectangles to represent 0.4. He then crossed out 3 of rectangles to represent the subtraction, leaving 1 rectangle in his diagram.

-
Do you agree that either diagram correctly represents \(0.4 - 0.03\)? Discuss your reasoning with a partner.
-
To represent \(0.4 - 0.03\), Elena drew another diagram. She also started by drawing 4 rectangles. She then replaced all 4 rectangles with 40 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 37 squares in her diagram. Is her diagram correct? Discuss your reasoning with a partner.
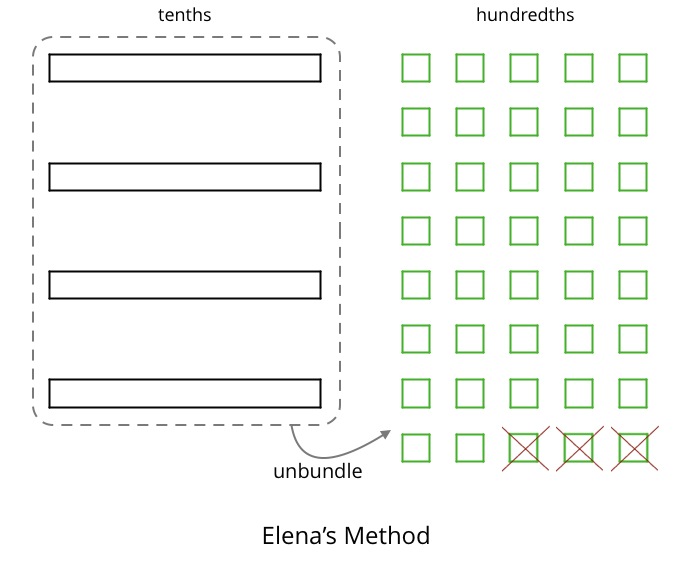
- Find each difference. If you get stuck, you can use the applet to represent each expression and find its value.
- \(0.3 - 0.05\)
- \(2.1 - 0.4\)
- \(1.03 - 0.06\)
- \(0.02 - 0.007\)
Be prepared to explain your reasoning.
- The applet has tools that create each of the base-ten blocks. This time you need to decide the value of each block before you begin.
- Select a Block tool, and then click on the screen to place it.
- Click on the Move tool (the arrow) when you are done choosing blocks.
- Subtract by deleting with the delete tool (the trash can), not by crossing out.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Keep students in the same groups of 2. Give partners 4–5 minutes to complete the first two questions. Then, give students 4–5 minutes of quiet time to complete the last question and follow with a whole-class discussion.


Use MLR2 (Collect and Display) to listen for and capture two or three different ways students refer to the idea of “unbundling” as they work on problems 1 and 2.
Supports accessibility for: Conceptual processing
Student Facing
Diego and Noah drew different diagrams to represent \(0.4 - 0.03\). Each rectangle represents 0.1. Each square represents 0.01.
- Diego started by drawing 4 rectangles to represent 0.4. He then replaced 1 rectangle with 10 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 3 rectangles and 7 squares in his diagram.

- Noah started by drawing 4 rectangles to represent 0.4. He then crossed out 3 rectangles to represent the subtraction, leaving 1 rectangle in his diagram.

-
Do you agree that either diagram correctly represents \(0.4 - 0.03\)? Discuss your reasoning with a partner.
- Elena also drew a diagram to represent \(0.4 - 0.03\). She started by drawing 4 rectangles. She then replaced all 4 rectangles with 40 squares and crossed out 3 squares to represent subtraction of 0.03, leaving 37 squares in her diagram. Is her diagram correct? Discuss your reasoning with a partner.

-
Find each difference. Explain or show your reasoning.
-
\(0.3 - 0.05\)
-
\(2.1 - 0.4\)
-
\(1.03 - 0.06\)
-
\(0.02 - 0.007\)
-
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.
At the Auld Shoppe, a shopper buys items that are worth 2 yellow jewels, 2 green jewels, 2 blue jewels, and 1 indigo jewel. If they came into the store with 1 red jewel, 1 yellow jewel, 2 green jewels, 1 blue jewel, and 2 violet jewels, what jewels do they leave with? Assume the shopkeeper gives them their change using as few jewels as possible.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to subtract two numbers that do not have the same number of decimal digits (such as in questions 3a and 3d), consider representing the subtraction with base-ten diagrams. For example, to illustrate \(0.3 - 0.05\), start by drawing 3 large rectangles to represent 3 tenths. Replace 1 rectangle with 10 squares, each representing 1 hundredth. Cross out 5 squares to show subtraction of 5 hundredths. Alternatively, replace 3 rectangles (3 tenths) with 30 squares (30 hundredths), cross out 5 squares to show subtraction of 5 hundredths.
Activity Synthesis
The purpose of this discussion is for students to make connections between two different and correct ways to subtract decimals when unbundling is required. Ask:
- “What is the difference between Diego’s method and Elena’s method?” (Diego only breaks up 1 tenth into 10 hundredths, whereas Elena breaks up all 4 tenths into hundredths.)
- “What are some advantages to Diego’s method?” (Diego’s method is quicker to draw. It shows the 3 tenths and 7 hundredths. Elena would need to count how many hundredths she has.)
- “What are some advantages to Elena’s method?” (Elena’s diagram shows a difference of 37 hundredths, which matches how we say 0.37 in words.)
Consider connecting the diagrams for Diego’s and Elena’s work with numerical equations as shown here.
| Diego’s | Elena’s |
|---|---|
|
0.4 - 0.03 |
0.4 - 0.03 = 0.40 - 0.03 = 0.37 |
We can also show both calculations by arranging the numbers vertically. On the left, the 3 and 10 in red show Diego’s unbundling of the 4 hundredths. The calculation on the right illustrates Elena’s representation: the 0 written in blue helps us see 4 tenths as 40 hundredths, from which we can subtract 3 hundredths to get 37 hundredths. Use this example to reinforce that writing an additional zero at the end of a non-zero decimal does not change its value.
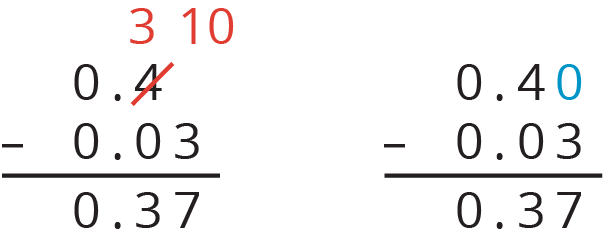
To deepen students’ understanding, consider asking:
- “In the problem \(2.1 - 0.4\), how does unbundling in the diagram show up in the vertical calculation with numbers?” (In the diagram, we unbundle 1 whole to make 10 tenths. With the calculation, we rewrite 1 whole as 10 tenths (over the tenth place) and combine it to the given 1 tenth before subtracting 4 tenths.)
- “When might it be really cumbersome to subtract using base-ten diagrams? Can you give examples?” (When the numbers involve many decimal places, such as \(113.004 - 6.056802\), or a problem with large digits, such as \(7.758 - 0.869\).)
Emphasize that the algorithm (vertical calculation) for subtraction of decimals works like the algorithm for subtraction of whole numbers. The only difference is that the values involved in the subtraction problems can now include tenths, hundredths, thousandths, and so on. The key in both cases is to pay close attention to the place values of the digits in the two numbers.
Lesson Synthesis
Lesson Synthesis
In this lesson, we saw that decimal subtraction problems can be done with base-ten diagrams or with vertical calculations. In both cases, it is important to subtract the values that are in the same decimal place. We also saw that zeros can be written to or removed from the end of a decimal without changing the value of the number.
- When using base-ten blocks to represent subtraction of decimals, how do we remove a larger value from a smaller value that are in the same decimal place? For example, to find \(4.5 - 2.7\), how do we remove 7 tenths from 5 tenths? (We unbundle a larger unit into 10 of a smaller unit; in this case, we exchange a 1 with 10 tenths, which allows us to subtract 7 tenths.)
- When calculating differences of decimals, why should we line up the decimal points or digits in the same decimal places? (The value of any digit in a base-ten number depends on its place. Lining up the decimal points and like units help us subtract correctly.)
- How do we subtract a number with more decimal places with one with fewer decimal places (e.g., \(4.1 - 1.0935\))? (We can write zeros at the end of the shorter decimal to help us subtract.)
- Which are more efficient for finding differences, using base-ten diagrams or using vertical calculations? (It depends on the length of the number and the size of the digits. Base-ten diagrams may take a while to draw.)
3.4: Cool-down - Calculate the Difference (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Base-ten diagrams can help us understand subtraction as well. Suppose we are finding \(0.23 - 0.07\). Here is a diagram showing 0.23, or 2 tenths and 3 hundredths.

Subtracting 7 hundredths means removing 7 small squares, but we do not have enough to remove. Because 1 tenth is equal to 10 hundredths, we can “unbundle” (or decompose) one of the tenths (1 rectangle) into 10 hundredths (10 small squares).
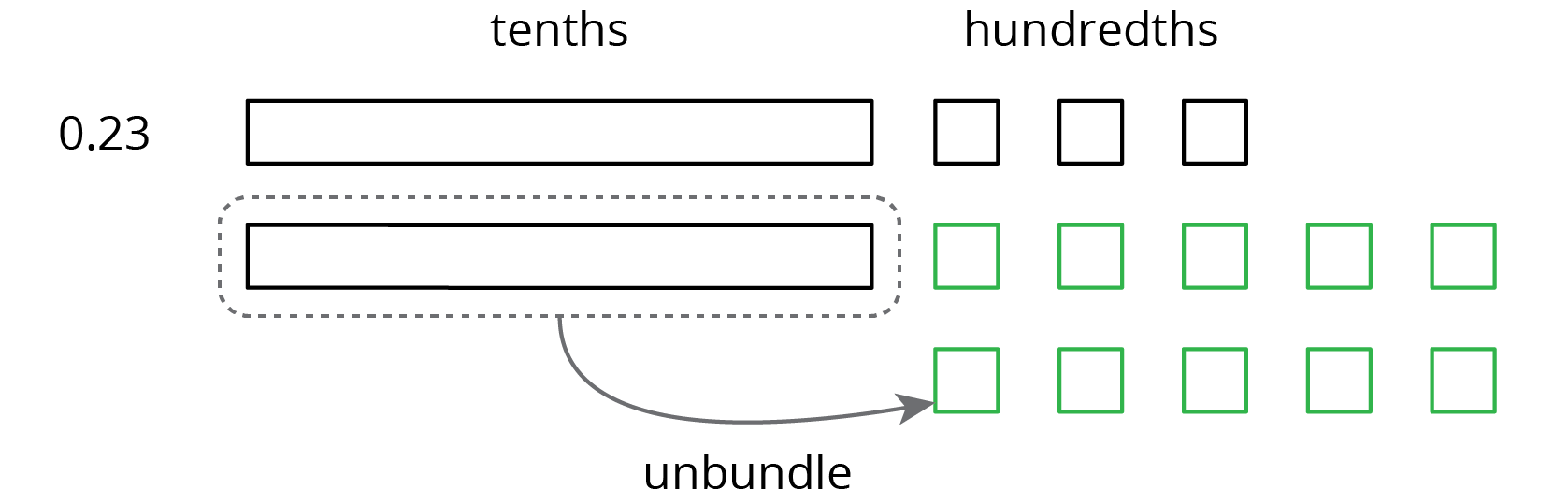
We now have 1 tenth and 13 hundredths, from which we can remove 7 hundredths.

We have 1 tenth and 6 hundredths remaining, so \(0.23 - 0.07 = 0.16\).

Here is a vertical calculation of \(0.23 - 0.07\).
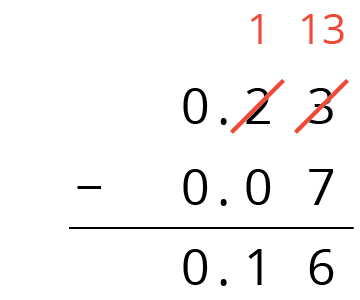
Notice how this representation also shows a tenth is unbundled (or decomposed) into 10 hundredths in order to subtract 7 hundredths.
This works for any decimal place. Suppose we are finding \(0.023 - 0.007\). Here is a diagram showing 0.023.

We want to remove 7 thousandths (7 small rectangles). We can “unbundle” (or decompose) one of the hundredths into 10 thousandths.
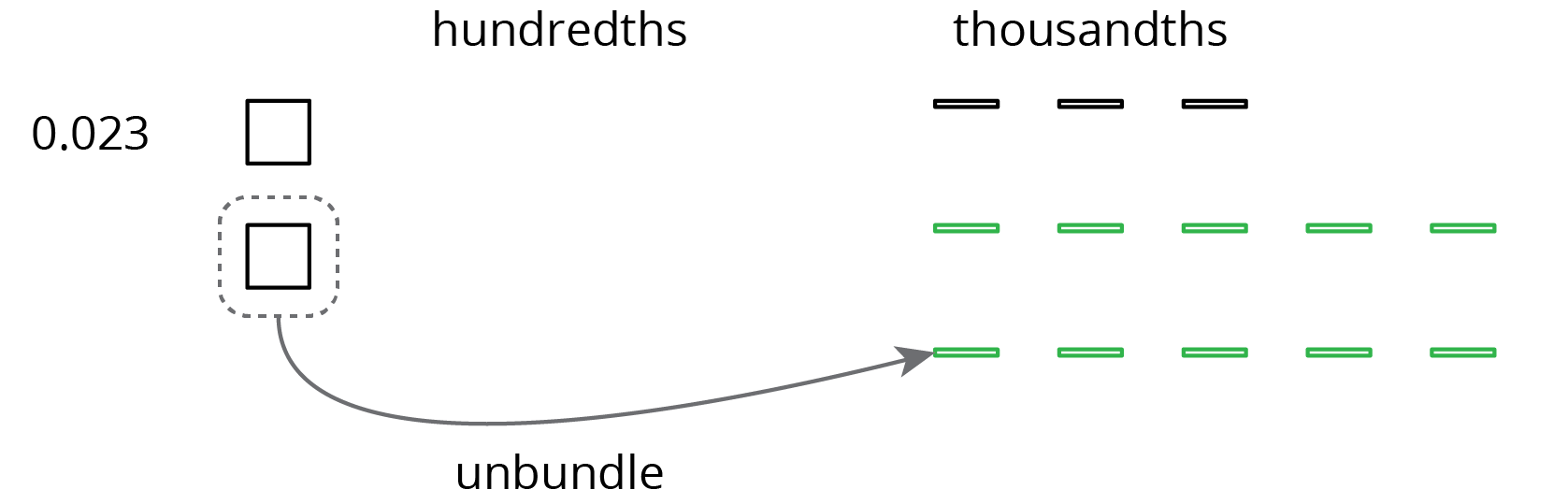
Now we can remove 7 thousandths.

We have 1 hundredth and 6 thousandths remaining, so \(0.023 - 0.007 = 0.016\).

Here is a vertical calculation of \(0.023 - 0.007\).