Lesson 9
Using the Partial Quotients Method
9.1: Using Base-Ten Diagrams to Calculate Quotients (5 minutes)
Warm-up
Prior to grade 6, students have solved division problems using their understanding of place value and the idea of creating equal-size groups. This warm-up relies on those concepts to prepare students for more-abstract work in later lessons. The divisor and dividend are chosen so that the hundreds in the dividend can be partitioned into equal groups but the tens cannot. The quotient, however, is a whole number. The key ideas that would enable students to ultimately divide a decimal by a decimal are present in this example:
- A number can be decomposed to make the division convenient, e.g., 372 can be viewed as 300 + 60 + 12.
- Place value, expressed in the form of base-ten diagrams, plays a very important role in division.
Launch
Arrange students in groups of 2. Display Elena’s method for all to see and use as a reference. Give students 1 minute of quiet think time and 2 minutes to discuss with a partner. Follow with a whole-class discussion.
Student Facing
Elena used base-ten diagrams to find \(372 \div 3\). She started by representing 372.

She made 3 groups, each with 1 hundred. Then, she put the tens and ones in each of the 3 groups. Here is her diagram for \(372 \div 3\).
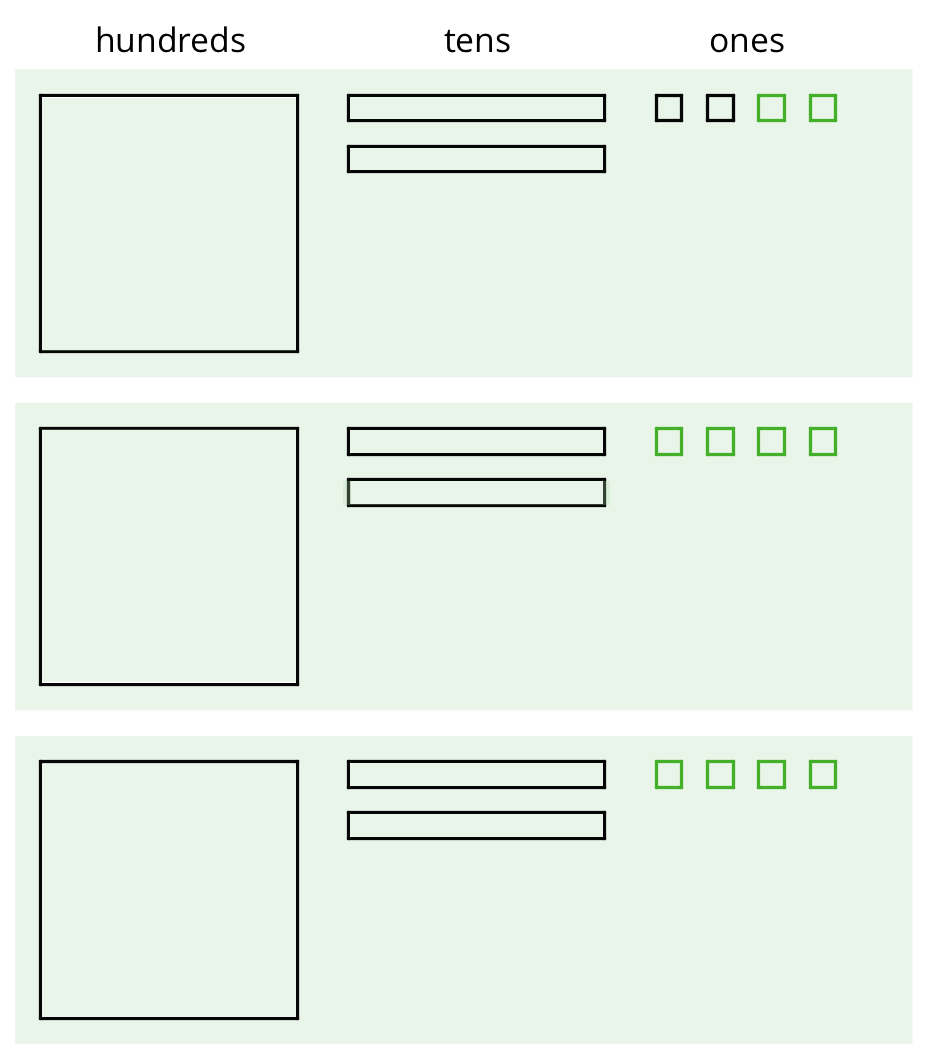
- Elena’s diagram for 372 has 7 tens. The one for \(372 \div 3\) has only 6 tens. Why?
- Where did the extra ones (small squares) come from?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have difficulty making sense of Elena’s method, consider demonstrating her process with actual base-ten blocks or paper cutouts.
Activity Synthesis
Highlight Elena’s process of separating base-ten units into equal groups. Discuss:
- Which base-ten unit(s) did Elena unbundle or break up? (She unbundled a tens unit.)
- Why? What did unbundling accomplish? (She had only 1 ten left and there are 3 equal groups. Unbundling as smaller units made it possible to place the 1 ten in the 3 groups.)
- Is there another way that Elena could have made 3 equal groups out of the base-ten units? (She could have unbundled other larger units into smaller units—e.g., the 3 hundreds as 30 tens or all 7 tens as 70 ones—but it was not necessary.)
- How might one find \(378 \div 3\) using Elena’s method? (By thinking of 378 as 3 hundreds, 6 tens, and 18 ones and placing them into 3 equal groups.)
9.2: Using the Partial Quotients Method to Calculate Quotients (15 minutes)
Activity
Here, students continue to find quotients of whole numbers by thinking about equal-size groups and place value. They learn that, in addition to using base-ten diagrams, they can also form equal-size groups using only numbers and by thinking in terms of partial quotients. Just as they had used diagrams to place base-ten units—first hundreds, then tens, and then ones—into equal groups until all units are placed, they can distribute base-ten units of a number into equal groups until all of the units are placed.
Launch
Keep students in groups of 2. Display the following diagram for all to see, and explain that it shows Elena’s method of finding \(657 \div 3\). Give students a minute to analyze the diagram, determine what the quotient is, and be prepared to explain what the diagram shows.
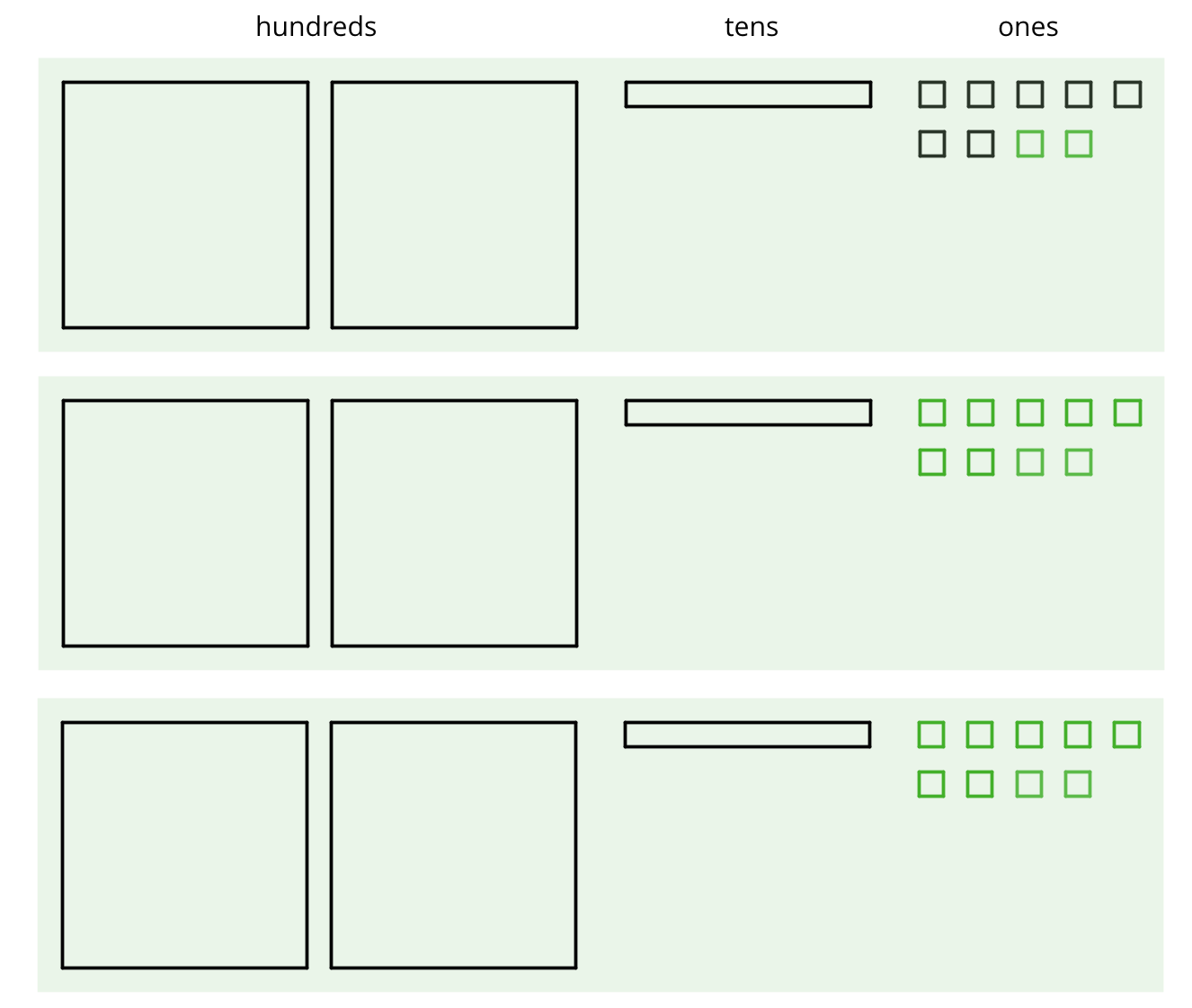
Give partners 1 minute to discuss their understanding of the diagram. Afterwards, consider asking a student to share with the class. Look for an explanation along the lines of the following:
- First, use the 6 hundreds to make 3 equal groups of 200.
- Then use 3 tens of the 5 tens to make 3 equal groups of 10.
- Unbundle the remaining 2 tens into 20 ones, combine them with the 7 ones, and split the 27 ones into 3 equal groups of 9.
If time permits, invite other students to elaborate on the presented explanations or share alternative analyses.
Keep Elena’s method from the previous task displayed for students to reference. Give students 7–8 minutes to think about and discuss Andre’s method in the first question and to complete the activity.
Provide access to graph paper. Tell students that they may find the grid helpful for aligning the digits when finding partial quotients.
Supports accessibility for: Visual-spatial processing
Design Principle(s): Cultivate conversation; Maximize meta-awareness
Student Facing
-
Andre calculated \(657 \div 3\) using a method that was different from Elena’s.

- Andre subtracted 600 from 657. What does the 600 represent?
- Andre wrote 10 above the 200, and then subtracted 30 from 57. How is the 30 related to the 10?
- What do the numbers 200, 10, and 9 represent?
- What is the meaning of the 0 at the bottom of Andre’s work?
-
How might Andre calculate \(896 \div 4\)? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
When using the partial quotients method, students might make subtraction or multiplication errors because they did not line up the numbers appropriately. Prompt students to compare the structure of Andre’s work with their own or to check if they have aligned like units in their vertical calculations.
Activity Synthesis
Make sure students understand how the steps in Elena’s method and Andre’s method correspond. Discuss:
- Elena’s diagram shows 3 groups of 2 hundreds. Where in Andre’s method do we see the same value? (In the 600 subtracted from 657.)
- Where in Elena’s work do we see the 30 that Andre subtracts from 57? (In the 3 groups of 1 ten.)
- Do Andre and Elena both get the same answer? Why? (Yes, because they both distributed 657 into 3 equal groups.)
Tell students that Andre’s method is an example of the partial quotients method, in which we divide a part of the dividend at a time, obtaining part of the quotient each time. In this case, the first partial quotient is 200, next is 210 (from \(200+10\)), and last is the quotient 219 (from \(200+10+9\)). We can still view a division expression such as \(657 \div 3\) as a question asking “How many are in each group if I divide 657 into 3 equal groups?”
With the partial quotients method, we can take any amount we choose out of 657 and place it into the 3 equal groups. It is often helpful to take out the amount in each place value and distribute it into groups. The values placed in each group are partial quotients. Once we have distributed all of 657, we can add the partial quotients to find \(657 \div 3\).
If time allows, discuss how to find the value of \(655 \div 5\) using the partial quotients method. Ask students what value might be reasonable to take out first, second, etc. (e.g., taking out 100 or 120 is a reasonable first move).
9.3: What’s the Quotient? (15 minutes)
Activity
In this lesson, students choose how to perform division—by drawing diagrams or by using the partial quotients method. As they work with larger dividends and divisors, students observe the merits and potential drawbacks of each method. They see that base-ten diagrams are useful because they are concrete and help to visualize the meaning of division, but drawing all the pieces is cumbersome if the numbers are large. The partial quotients method relies on the same principles but will work for any numbers without the need for elaborate drawings. Students use these observations to decide on appropriate methods to use.
Earlier, when introducing Andre’s method and partial quotients, we had interpreted \(657 \div 3\) as answering the question: “How much is in each group if 657 is divided into 3 equal groups?” For example, when Andre took out 600, we interpreted it as: “600 is 3 groups of 200.” This interpretation is helpful for making the connection to Elena’s base-ten diagrams, in which she divided base-ten units into 3 groups.
Note, however, that we can also interpret the division expression as asking: “How many groups of 3 are in 657?” This interpretation can likewise be represented using diagrams, though it would be highly impractical to draw 219 groups of 3. It is not impractical for students to think about partial quotients this way, however. For instance, they could take out 600, ask “how many groups of 3 are in 600?” and write down a partial quotient of 200 to represent 200 groups of 3 (instead of 3 groups of 200).
Launch
Remind students that Elena drew base-ten diagrams to represent equal groups, while Andre took out smaller amounts from the dividend, found those quotients, and then combined the partial quotients together. Tell students that in this activity they choose a method to perform division. Encourage them to refer to Elena and Andre’s methods from the previous activities, or display Elena and Andre’s methods for all to see.
Keep students in groups of 2. Give students 2–3 minutes to discuss the first question with a partner and 8–10 minutes of quiet work time on the remaining questions. Provide access to graph paper.
Supports accessibility for: Conceptual processing
Student Facing
- Find the quotient of \(1,\!332 \div 9\) using one of the methods you have seen so far. Show your reasoning.
-
Find each quotient and show your reasoning. Use the partial quotients method at least once.
- \(1,\!115 \div 5\)
- \(665 \div 7\)
- \(432 \div 16\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Focus the discussion on showcasing the advantages and disadvantages of each method. Ask students to indicate which division method they preferred for the first two problems. Then, ask students who used base-ten diagrams to share the challenges of using this method to divide. Possible responses include:
- When the divisor is large, it takes a long time to draw all of the equal groups.
- When the dividend or divisor is large, it is difficult to tell how much I have used up or placed in groups and how much remains.
- When the dividend or divisor is large, it is difficult to check my work, i.e., to see that all of the equal groups add up to the value of the dividend.
Ask students who used the partial quotients to name the challenges of using this method for division? Possible responses include:
- I was not sure how to decide what amount to take out at each step.
- Sometimes I could not find familiar numbers to take out.
- I took out too little at a time, so it ended up taking a long time.
- I thought I had placed everything into equal groups but I ended up with a leftover.
Show that many of the challenges of using base-ten diagrams are eliminated by using the partial quotients method and explain that in future lessons the partial quotients method will be refined to help deal with its challenges.
Design Principle(s): Optimize output (for comparison); Maximize meta-awareness
Lesson Synthesis
Lesson Synthesis
Recall that one way to think of division is as a process of splitting a value into equal-size groups and finding the size of one group. We can represent the groups and contents of each group using base-ten diagrams. Let’s take \(456 \div 4\) as an example. We start by representing 456 with drawings of 4 hundreds, 5 tens, and 6 ones.
- How might we start dividing the pieces? (We can do it by place value. We draw 4 groups, put 1 hundred into each group, and then put 1 ten into each group.)
- What happens if there’s a remainder, e.g., after putting 1 ten into each group, we still have 1 ten left? (We can unbundle the 1 ten into 10 ones.)
- What does unbundling accomplish? (It allows us to have smaller units to divide. Here we combine the 10 ones and 6 ones, and then divide 16 ones into 4 groups of 4.)
- How do we find the value of the quotient? (The value of all the pieces in each group is the quotient.)
We can also find quotients without drawing a diagram and by using the partial quotients method.
- How is the partial quotient method similar to drawing base-ten diagrams? (We still pay attention to place value and think in terms of equal-size groups.)
- How is it different than drawing diagrams? (With partial quotients, we use only numbers, and we don’t have to divide the entirety of each base-ten unit at once. We can decide the amount to divide each round, e.g., we could first divide 200 into 4 groups, then another 200 into 4 groups, etc.)
- What might be the advantages of using base-ten diagrams? (It is concrete. It helps us visualize the number being divided.)
- What are the advantages of using partial quotients to divide numbers? (There is no need to draw all the pieces being divided or all the groups. There is flexibility in how we divide.)
- Do you have a preferred method for finding decimal quotients? Explain your reasoning.
9.4: Cool-down - Dividing by 11 (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can find the quotient \(345\div 3\) in different ways.
One way is to use a base-ten diagram to represent the hundreds, tens, and ones and to create equal-sized groups.

We can think of the division by 3 as splitting up 345 into 3 equal groups.
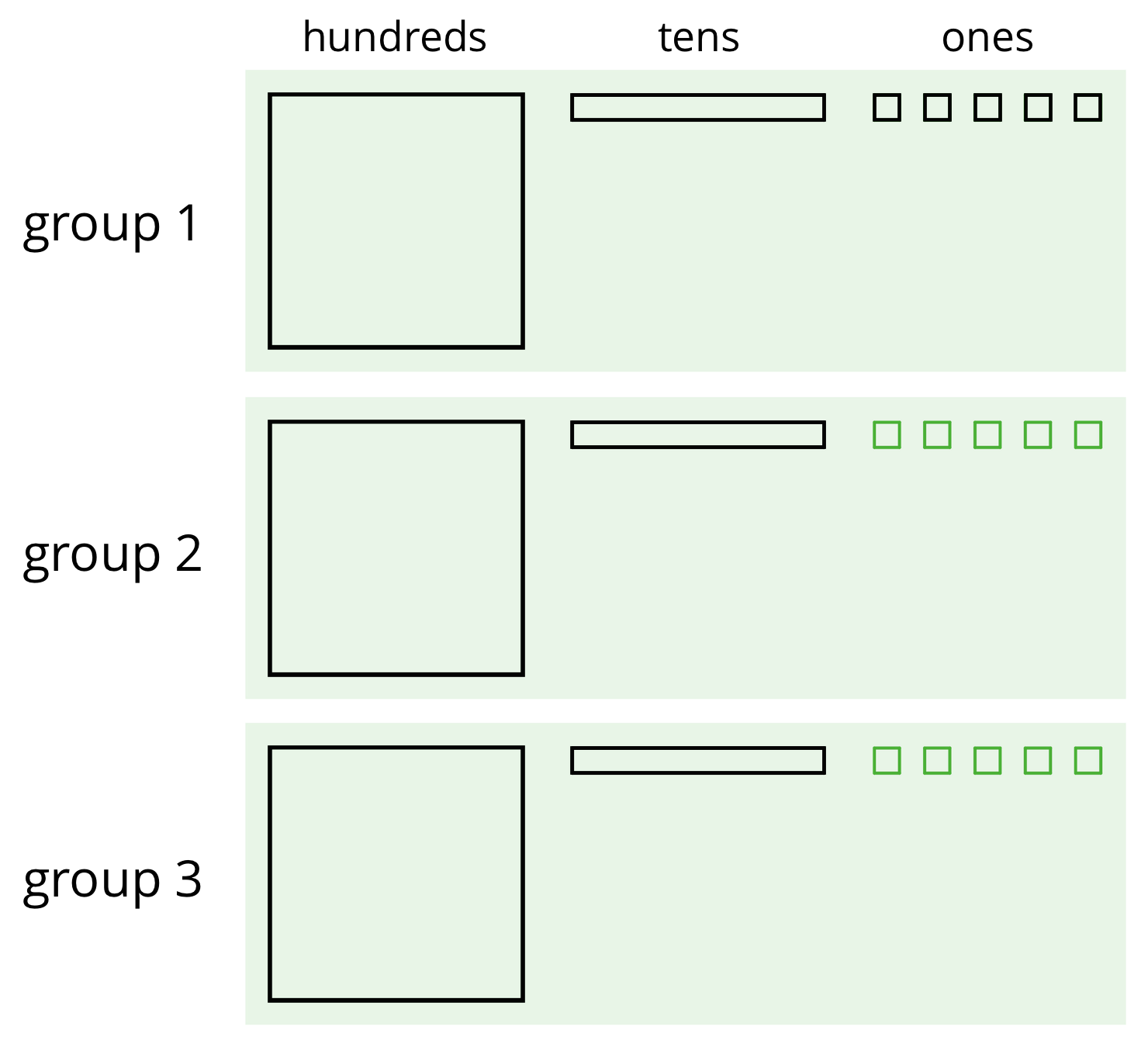
Each group has 1 hundred, 1 ten, and 5 ones, so \(345 \div 3 = 115\). Notice that in order to split 345 into 3 equal groups, one of the tens had to be unbundled or decomposed into 10 ones.
Another way to divide 345 by 3 is by using the partial quotients method, in which we keep subtracting 3 groups of some amount from 345.
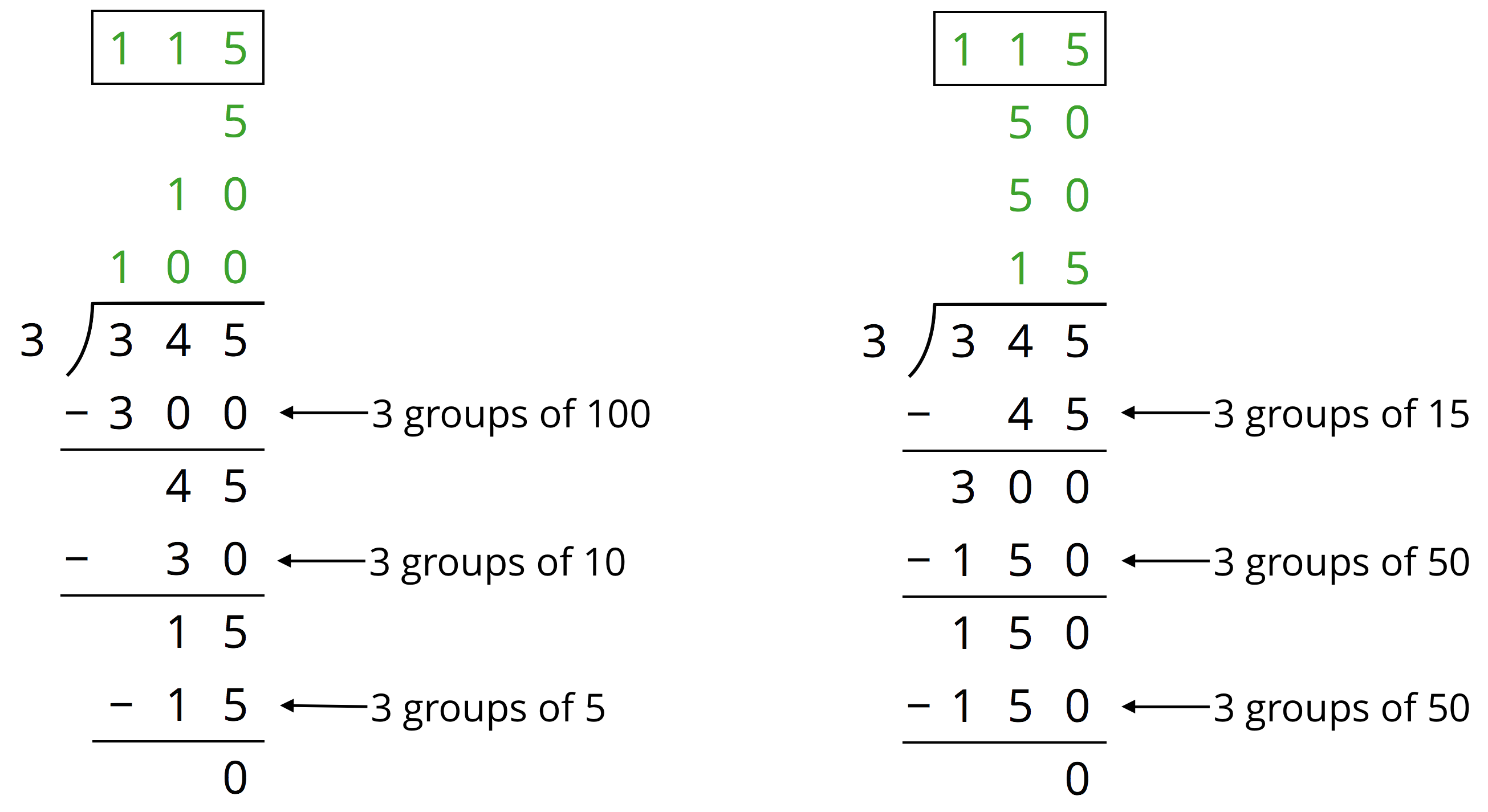
- In the calculation on the left, first we subtract 3 groups of 100, then 3 groups of 10, and then 3 groups of 5. Adding up the partial quotients (\(100+10+5\)) gives us 115.
- The calculation on the right shows a different amount per group subtracted each time (3 groups of 15, 3 groups of 50, and 3 more groups of 50), but the total amount in each of the 3 groups is still 115. There are other ways of calculating \(345 \div 3\) using the partial quotients method.
Both the base-ten diagrams and partial quotients methods are effective. If, however, the dividend and divisor are large, as in \(1,\!248 \div 26\), then the base-ten diagrams will be time-consuming.