Lesson 2

Using Diagrams to Represent Addition and Subtraction

View Student Lesson

Problem 1

Use the given key to answer the questions.

Base-ten figures.
  1. What number does this diagram represent?
    A base-ten diagram. 2 squares, 5 small rectangles.

  2. Draw a diagram that represents 0.216.

  3. Draw a diagram that represents 0.304.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Here are diagrams that represent 0.137 and 0.284.

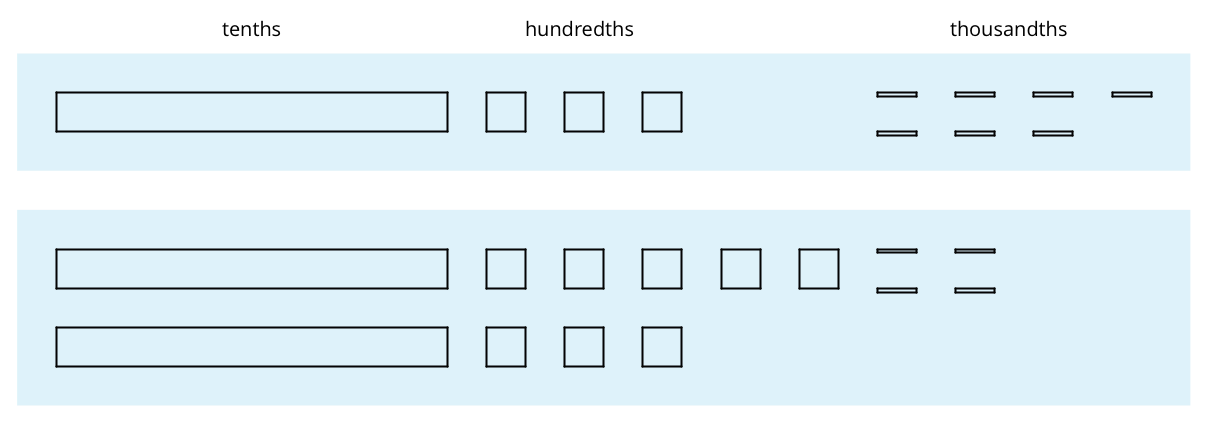
Two base-ten diagrams representing 0 point 1 3 7 and 0 point 2 8 4.
  1. Use the diagram to find the value of \(0.137 + 0.284\). Explain your reasoning.

  2. Calculate the sum vertically.

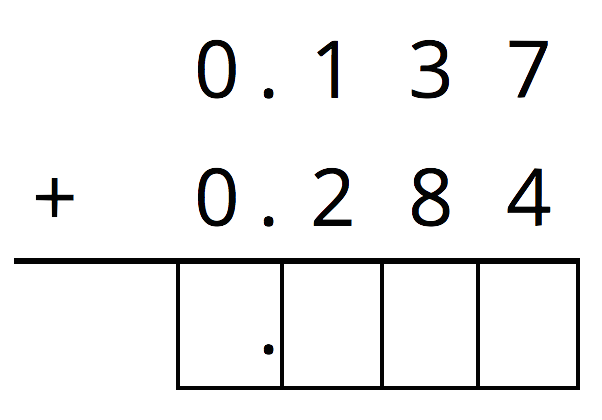
    Calculation with missing digits. 0 point 1 3 7 plus 0 point 2 8 4 is equal to an unknown quantity with four digits.

  3. How was your reasoning about \(0.137 + 0.284\) the same with the two methods? How was it different?

Solution

For access, consult one of our IM Certified Partners.

Problem 3

For the first two problems, circle the vertical calculation where digits of the same kind are lined up. Then, finish the calculation and find the sum. For the last two problems, find the sum using vertical calculation.

  1. \(3.25+1\)

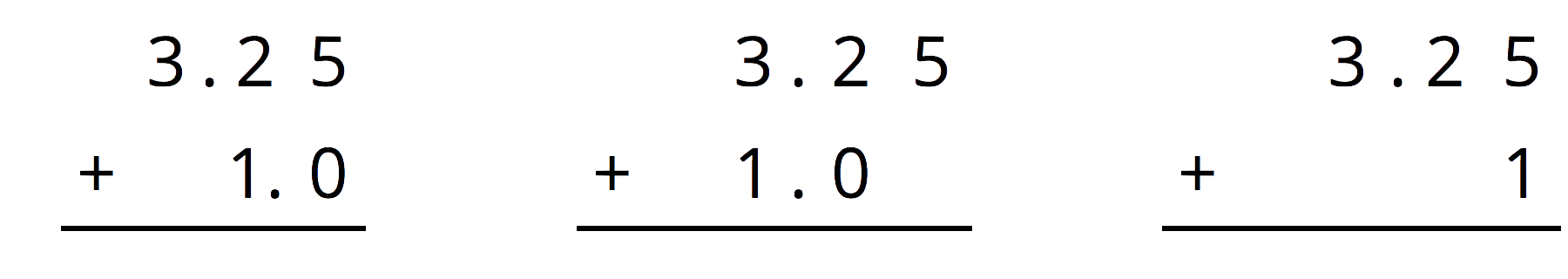
    3 vertical calculations of 3 point 2 5 plus 1.

  2. \(0.5+1.15\)

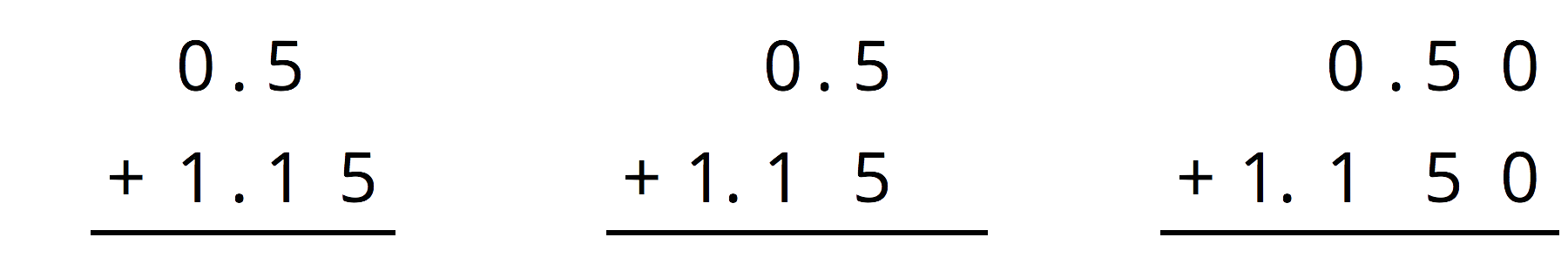
    3 vertical calculations of 0 point 5 plus 1 point 1 5.

  3. \(10.6+ 1.7\)

  4. \(123+0.2\)

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Andre has been practicing his math facts. He can now complete 135 multiplication facts in 90 seconds.

  1. If Andre is answering questions at a constant rate, how many facts can he answer per second?
  2. Noah also works at a constant rate, and he can complete 75 facts in 1 minute. Who is working faster? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 9.)