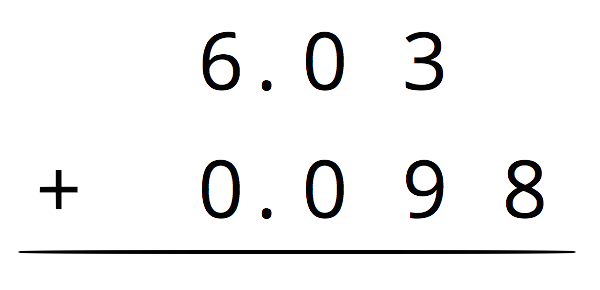Lesson 2
Using Diagrams to Represent Addition and Subtraction
Let’s represent addition and subtraction of decimals.
2.1: Changing Values
- Here is a rectangle.

What number does the rectangle represent if each small square represents:
-
1
-
0.1
-
0.01
-
0.001
-
- Here is a square.

What number does the square represent if each small rectangle represents:
-
10
-
0.1
- 0.00001
-
2.2: Squares and Rectangles
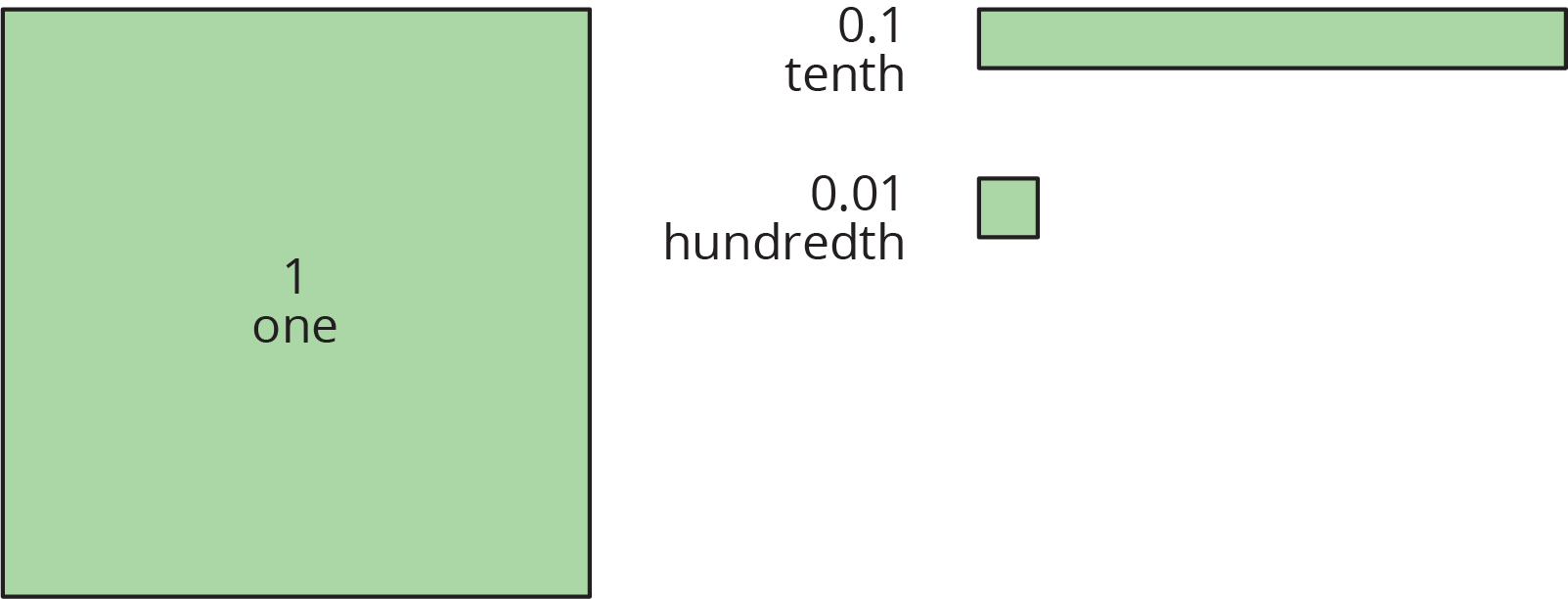
You may be familiar with base-ten blocks that represent ones, tens, and hundreds. Here are some diagrams that we will use to represent digital base-ten units. A large square represents 1 one. A rectangle represents 1 tenth. A small square represents 1 hundredth.
The applet has tools that create each of the base-ten blocks.
Select a Block tool, and then click on the screen to place it.

One

Tenth

Hundredth
Click on the Move tool when you are done choosing blocks.

-
Here is the diagram that Priya drew to represent 0.13. Draw a different diagram that represents 0.13. Explain why your diagram and Priya’s diagram represent the same number.

-
Here is the diagram that Han drew to represent 0.25. Draw a different diagram that represents 0.25. Explain why your diagram and Han’s diagram represent the same number.
-
For each of these numbers, draw or describe two different diagrams that represent it.
- 0.1
- 0.02
- 0.43
-
Use diagrams of base-ten units to represent the following sums and find their values. Think about how you could use as few units as possible to represent each number.
-
\(0.03 + 0.05\)
-
\(0.06 + 0.07\)
-
\(0.4 + 0.7\)
-
2.3: Finding Sums in Different Ways
-
Here are two ways to calculate the value of \(0.26 + 0.07\). In the diagram, each rectangle represents 0.1 and each square represents 0.01.

Use what you know about base-ten units and addition of base-ten numbers to explain:
-
Why ten squares can be “bundled” into a rectangle.
-
How this “bundling” is reflected in the computation.
The applet has tools that create each of the base-ten blocks. Select a Block tool, and then click on the screen to place it.

One

Tenth

Hundredth
Click on the Move tool when you are done choosing blocks.

-
-
Find the value of \(0.38 + 0.69\) by drawing a diagram. Can you find the sum without bundling? Would it be useful to bundle some pieces? Explain your reasoning.
-
Calculate \(0.38 + 0.69\). Check your calculation against your diagram in the previous question.
-
Find each sum. The larger square represents 1, the rectangle represents 0.1, and the smaller square represents 0.01.
-
A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.
-
If you had 500 violet jewels and wanted to trade so that you carried as few jewels as possible, which jewels would you have?
-
Suppose you have 1 orange jewel, 2 yellow jewels, and 1 indigo jewel. If you’re given 2 green jewels and 1 yellow jewels, what is the fewest number of jewels that could represent the value of the jewels you have?
2.4: Representing Subtraction
-
Here are diagrams that represent differences. Removed pieces are marked with Xs. The larger rectangle represents 1 tenth. For each diagram, write a numerical subtraction expression and determine the value of the expression.

-
Express each subtraction in words.
-
\(0.05 - 0.02\)
-
\(0.024 - 0.003\)
-
\(1.26 - 0.14\)
-
-
Find each difference by drawing a diagram and by calculating with numbers. Make sure the answers from both methods match. If not, check your diagram and your numerical calculation.
-
\(0.05 - 0.02\)
-
\(0.024 - 0.003\)
- \(1.26 - 0.14\)
-
Summary
Base-ten diagrams represent collections of base-ten units—tens, ones, tenths, hundredths, etc. We can use them to help us understand sums of decimals.
Suppose we are finding \(0.08 + 0.13\). Here is a diagram where a square represents 0.01 and a rectangle (made up of ten squares) represents 0.1.

To find the sum, we can “bundle” (or compose) 10 hundredths as 1 tenth.
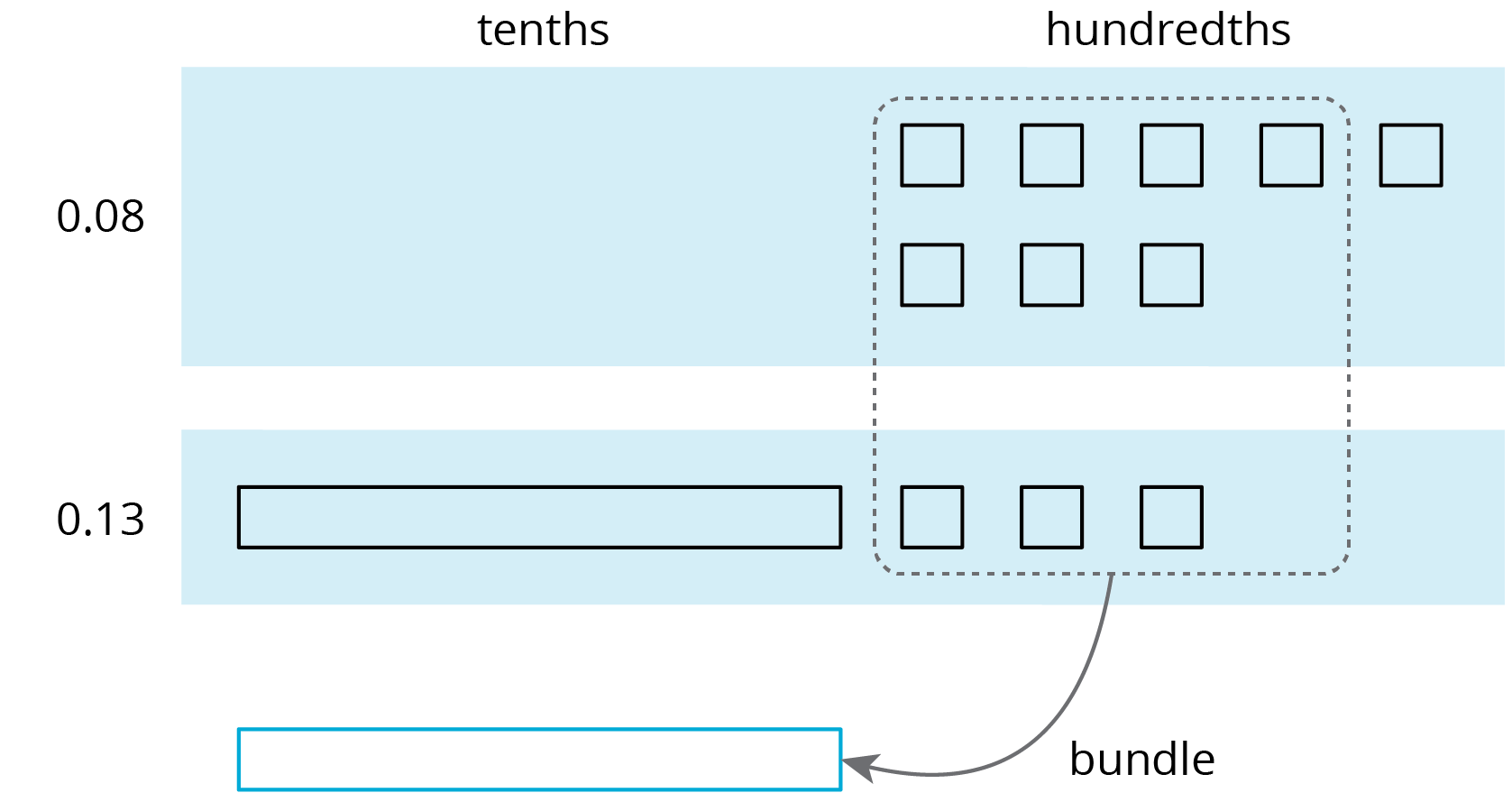
We now have 2 tenths and 1 hundredth, so \(0.08 + 0.13 = 0.21\).

We can also use vertical calculation to find \(0.08 + 0.13\).

Notice how this representation also shows 10 hundredths are bundled (or composed) as 1 tenth.
This works for any decimal place. Suppose we are finding \(0.008 + 0.013\). Here is a diagram where a small rectangle represents 0.001.
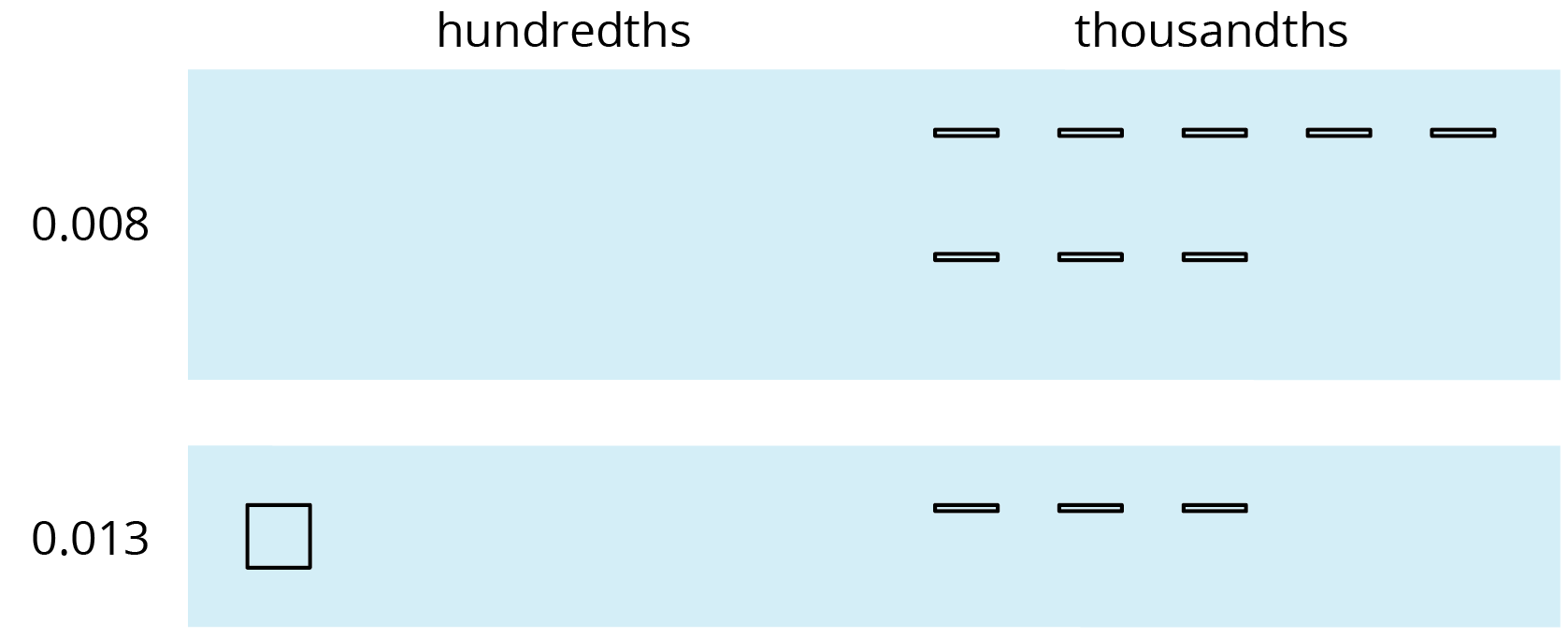
We can “bundle” (or compose) 10 thousandths as 1 hundredth.
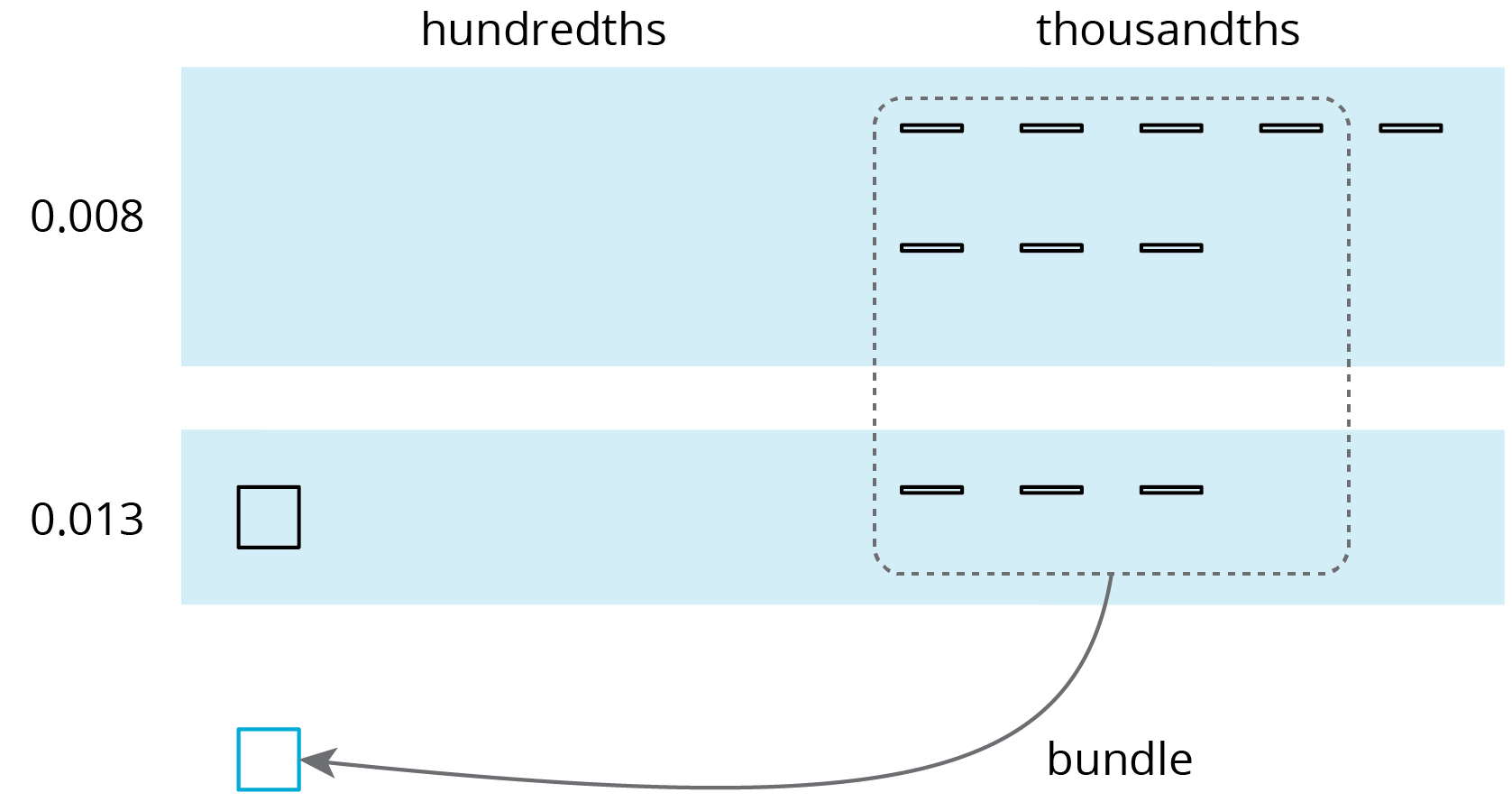
The sum is 2 hundredths and 1 thousandth.

Here is a vertical calculation of \(0.008 + 0.013\).