Lesson 15

Volume of Prisms

View Student Lesson

Problem 1

A pool in the shape of a rectangular prism is being filled with water. The length and width of the pool is 24 feet and 15 feet. If the height of the water in the pool is \(1\frac13\) feet, what is the volume of the water in cubic feet?

Solution

For access, consult one of our IM Certified Partners.

Problem 2

A rectangular prism measures \(2\frac25\) inches by \(3\frac15\) inches by 2 inch.

  1. Priya said, “It takes more cubes with edge length\(\frac25\) inch than cubes with edge length \(\frac15\) inch to pack the prism.” Do you agree with Priya? Explain or show your reasoning.

  2. How many cubes with edge length \(\frac15\) inch fit in the prism? Show your reasoning.

  3. Explain how you can use your answer in the previous question to find the volume of the prism in cubic inches.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

  1. Here is a right triangle. What is its area?

  2. What is the height \(h\) for the base that is \(\frac54\) units long? Show your reasoning.

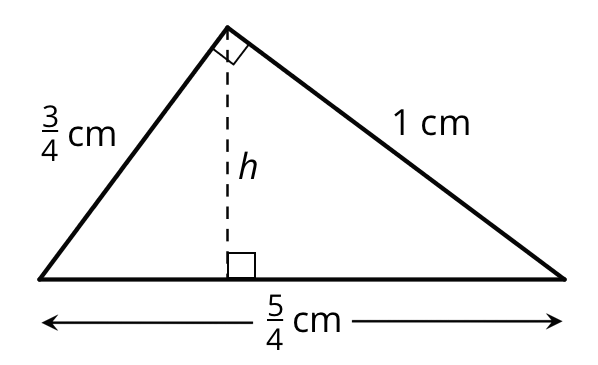
A right triangle. 

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 14.)

Problem 4

To give their animals essential minerals and nutrients, farmers and ranchers often have a block of salt—called “salt lick”—available for their animals to lick.

  1. A rancher is ordering a box of cube-shaped salt licks. The edge lengths of each salt lick are \(\frac{5}{12}\) foot. Is the volume of one salt lick greater or less than 1 cubic foot? Explain your reasoning.

    A image of a salt-lick.
  2. The box that contains the salt lick is \(1\frac14\) feet by \(1\frac23\) feet by \(\frac56\) feet. How many cubes of salt lick fit in the box? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

  1. How many groups of \(\frac13\) inch are in \(\frac34\) inch?
  2. How many inches are in \(1\frac25\) groups of \(1\frac23\) inches?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 12.)

Problem 6

Here is a table that shows the ratio of flour to water in an art paste. Complete the table with values in equivalent ratios.

cups of flour cups of water
1 \(\frac12\)
4
3
\(\frac12\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 12.)